2.2 Dropout在神经网络中的使用
Dropout的具体工作流程上面已经详细的介绍过了,但是具体怎么让某些神经元以一定的概率停止工作(就是被删除掉)?代码层面如何实现呢?
下面,我们具体讲解一下Dropout代码层面的一些公式推导及代码实现思路。
(1)在训练模型阶段
无可避免的,在训练网络的每个单元都要添加一道概率流程。
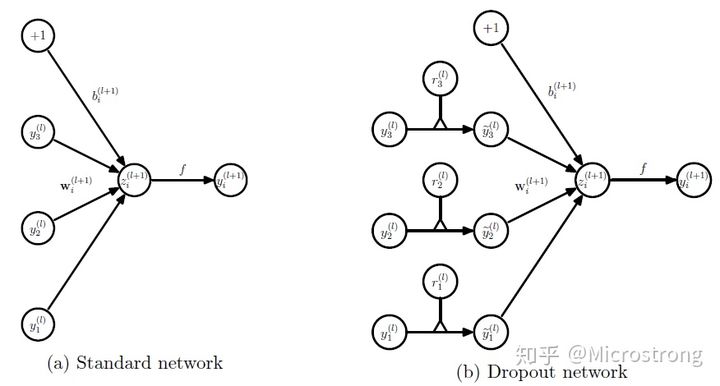
图4:标准网络和带有Dropout网络的比较
对应的公式变化如下:
- 没有Dropout的网络计算公式:
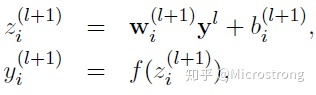
- 采用Dropout的网络计算公式:
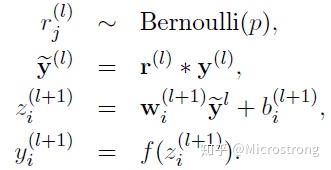
上面公式中Bernoulli函数是为了生成概率r向量,也就是随机生成一个0、1的向量。
代码层面实现让某个神经元以概率p停止工作,其实就是让它的激活函数值以概率p变为0。比如我们某一层网络神经元的个数为1000个,其激活函数输出值为y1、y2、y3、......、y1000,我们dropout比率选择0.4,那么这一层神经元经过dropout后,1000个神经元中会有大约400个的值被置为0。
注意: 经过上面屏蔽掉某些神经元,使其激活值为0以后,我们还需要对向量y1……y1000进行缩放,也就是乘以1/(1-p)。如果你在训练的时候,经过置0后,没有对y1……y1000进行缩放(rescale),那么在测试的时候,就需要对权重进行缩放,操作如下。
(2)在测试模型阶段
预测模型的时候,每一个神经单元的权重参数要乘以概率p。
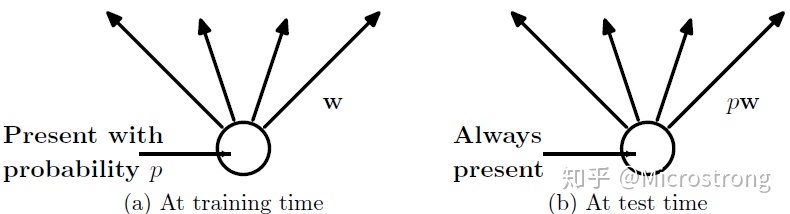
图5:预测模型时Dropout的操作
测试阶段Dropout公式:
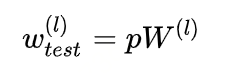
思考:上面我们介绍了两种方法进行Dropout的缩放,那么Dropout为什么需要进行缩放呢?
因为我们训练的时候会随机的丢弃一些神经元,但是预测的时候就没办法随机丢弃了。如果丢弃一些神经元,这会带来结果不稳定的问题,也就是给定一个测试数据,有时候输出a有时候输出b,结果不稳定,这是实际系统不能接受的,用户可能认为模型预测不准。那么一种”补偿“的方案就是每个神经元的权重都乘以一个p,这样在“总体上”使得测试数据和训练数据是大致一样的。比如一个神经元的输出是x,那么在训练的时候它有p的概率参与训练,(1-p)的概率丢弃,那么它输出的期望是px+(1-p)0=px。因此测试的时候把这个神经元的权重乘以p可以得到同样的期望。
总结:
当前Dropout被大量利用于全连接网络,而且一般认为设置为0.5或者0.3,而在卷积网络隐藏层中由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因,Dropout策略在卷积网络隐藏层中使用较少。总体而言,Dropout是一个超参,需要根据具体的网络、具体的应用领域进行尝试。