排序
排序(sorting)是根据某些标准,将一组数据项按确定的次序重排,或为升序或为降序,例如按字母表顺序排列名字,或按降序排列测量结果。排序被认为是计算机科学的经典研究领域。
我们在此研究5个不同的排序算法:选择排序、插入排序、冒泡排序、快速排序和归并排序。前三种算法的效率差不多,但方法都有所不同。后两种算法的效率更高,也相对比较复杂。我将在本文的最后一节简要介绍评估算法复杂度的方法并比较这些排序算法。
选择排序
选择排序(selection sort)算法重复一个过程:分别将每个值放到排好序的最终位置,从而完成一组值的排序。换句话说,对于表中的每个位置,算法选择应该处在那个位置的值,并将它放置到位。
选择排序算法反复地将一个个具体的值放到它最终的有序位置,从而完成一组值的排序。
选择排序的一般策略是:扫描整个表,找到最小值。将这个值与表中第一个位置的值相交换。然后扫描余下的表(除了第一个元素之外的所有值),找到最小值,将这个值与表中第二个位置的值相交换。对表中每个位置重复这个步骤,直到最后一个位置的值排序完毕。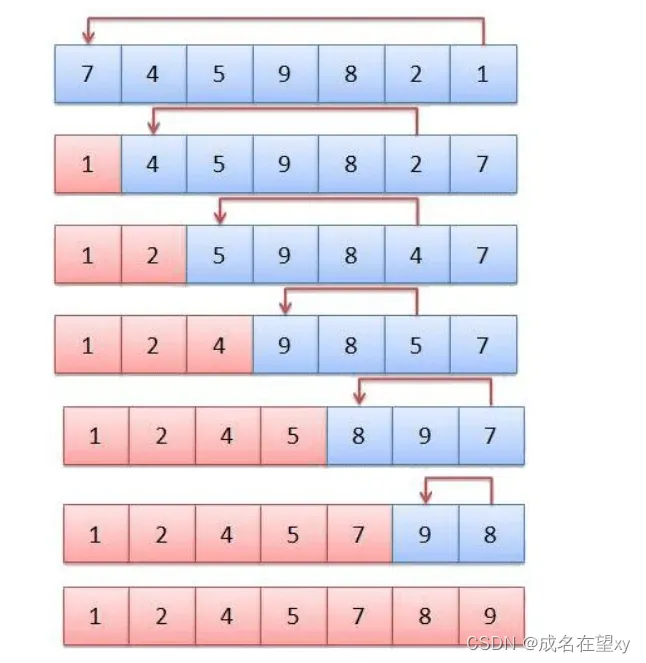
public static void selectionSort(Comparable[] data)
{
int min;
for (int index = 0; index < data.length-1; index++)
{
min = index;
for (int scan = index+1; scan < data.length; scan++)
{
if (data[scan].compareTo(data[min]) < 0)
min = scan;
swap(data, min, index);
}
}
}
上述selectionSort方法接受Comparable对象数组作为参数,当控制返回到调用方法位置时对象数组就完成了排序。方法使用了双重循环对数组进行排序,外层循环控制数组中下一个最小值要存储的位置。内层循环大于等于外层循环所指定的下标的所有位置,查找表中余下数据的最小值。当找到最小值时,将它与index指示的位置的元素进行互换。这个算法在每次迭代中查找最小值,所以排好序的数组呈升序形式,算法同样可以在每次循环时查找最大值,这样很容易就改为降序排列。
在数组中交换两个元素的操作由方法swap完成,该方法利用三个赋值语句来完成交换。
public static void swap(Comparable[] data, int index1, int index2)
{
Comparable temp = data[index1];
data[index1] = data[index2];
data[index2] = temp;
}
插入排序
插入排序(insertion sort)算法重复地将一个具体的值插入到表中已有序的子序列中,从而完成一组值的排序。每次将每个待排序的元素插入到有序子段中的适当位置,知道表中全部元素都有序为止。
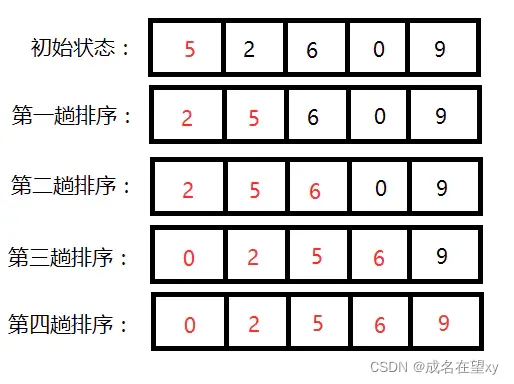
插入排序的一般策略是:对表最前面的两个元素进行排序,如果有必要就进行交换。将表中的第三个值插入到前两个值组成的已有序的子段中的合适位置。再将表中的第四个值插入到前面三个值的合适位置。像这样每次插入时,已有序的子段中的元素个数增加一个。重复前面的步骤直到表中所有的元素全部有序时为止。插入过程会要求数组中的其他元素都要向后移动,为新插入的元素腾出空间。
public static void insertionSort(Comparable[] data)
{
for (int index = 1; index < data.length; index++)
{
Comparable key = data[index];
int position = index;
while (positon > 0 && data[position-1].compareTo(key) > 0)
{
data[position] = data[position-1];
position--;
}
data[position] = key;
}
}
与选择排序的实现类似,insertionSort方法使用双重循环来排序对象数组。但在插入排序中,外层循环控制下一个待插入元素在数组中的下标。内层循环将当前待插入元素的值与它前面位置已构成有序子段的值进行比较。如果当前待插入元素小于position所指的位置的值,则将这个值右移。继续右移过程直到腾出一个合适的位置来放置待插入的元素,然后将这个元素放在这个位置。外层循环的每次迭代都使得表中有序子段延长一个元素,直到整个表有序时为止。
冒泡排序
冒泡排序(bubble sort)算法重复地比较表中的相邻元素,如果它们呈逆序则交换它们。
冒泡排序算法的一般策略是:扫描整个表,比较相邻元素,如果它们的相互次序不正确就交换它们。执行的结果是将最大值“冒泡”到表的最后为止,这也是它在有序表中的最终位置。然后再次扫描余下的表,将第二个最大值冒泡到它的最终位置。重复这个过程直到所有元素都冒泡到正确位置时为止。

public static void bubbleSort(Comparable[] data)
{
int position,scan;
for (position = data.length-1; position >= 0; position--)
{
for (scan = 0; scan <= position-1; scan++)
{
if (data[scan].compareTo(data[scan+1]) > 0)
swap(data,scan,scan+1);
}
}
}
bubbleSort方法实现了冒泡排序。外层循环表示对n个数据的n-1趟扫描。内层循环扫描数据,在相邻数据对之间进行比较,如有必要就交换它们。
注意,外层循环还使得内层循环中表示最大元素的下标位置减1。即在第一趟扫描将最大值放到正确位置后,不需要在后面的扫描中再次考虑这个值。在第二趟扫描后可以不考虑最后两个元素,以此类推。所以内层循环在每趟扫描中减少一个值。
快速排序
到前面为止的讨论都是一些相对简单并且效率不高的排序算法,它们全都使用一对嵌套的循环,对n个元素进行排序时大概需要进行n2次比较。下面我们来看一些更高效的排序算法。
快速排序(quick sort)算法根据一个任意选定的划分元素(partition element)来对表进行划分,然后再递归地对划分元素两边的子段进行排序,从而完成对整个表的排序。
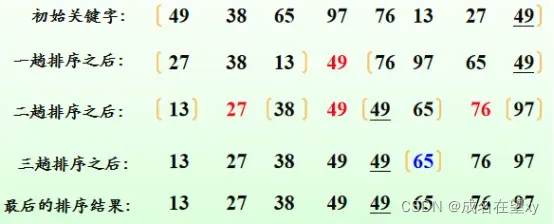
快速排序的一般策略是:先选择表中的一个元素作为划分元素。接下来对表进行划分,小于划分元素的所有元素放到划分元素的左侧,大于划分元素的所有元素放到它的右侧。再用这个快速排序的策略递归地对两个划分段进行排序。持续这个过程直到所有的划分段只包含一个元素为止,而一个元素自然有序。所以算法递归地应用于每一边后,整个表就有序了。
如果初始时待排序的项是随机排列的,则任意选取划分元素,可以由表的第一个元素担当。从效率角度考虑,如果划分元素能把表划分为大致相等的两部分就是最好的了,不过无论如何选取划分元素,算法本身都能正确执行。
public static void quickSort(Comparable[] data, int min, int max)
{
int pivot;
if (min < max)
{
pivot = partition(data, min, max);
quickSort(data, min, max);
quickSort(data, pivot+1, max);
}
}
private static int partition(Comparable[] data, int min, int max)
{
int left = min;
int right = max;
while (left < right)
{
while (data[left].compareTo(partitionValue) <= 0 && left < right)
left++;
while (data[right].compareTo(partitionValue) > 0)
right--;
if (left < right)
swap(data,left,right);
}
swap(data,min,right);
}
上述quickSort方法实现了快速排序算法。它接收待排序的一个对象数组,以及一次具体的方法调用时要用到的最小和最大下标。在首次调用方法时,min和max的值应该包含待排序的全部元素。
quickSort方法调用了一个支撑方法partition,它将元素划分到划分元素的两侧,并返回划分元素的最终下标,即枢轴点(pivot point)。然后,quickSort方法再调用自己两次,从而排序两个子段。当划分段中的元素不多于一个时,if语句终止递归过程。对于当前的划分段,partition方法从两端开始向中间扫描,直到它遇到两个错误放在两边的元素,然后交换它们。当这个过程在划分点相遇时,划分宣告完成。
归并排序
归并排序(merge sort)递归地对分表,直到每个子表只含有一个元素为止,然后再将子表按顺序合并,从而完成对表的排序。
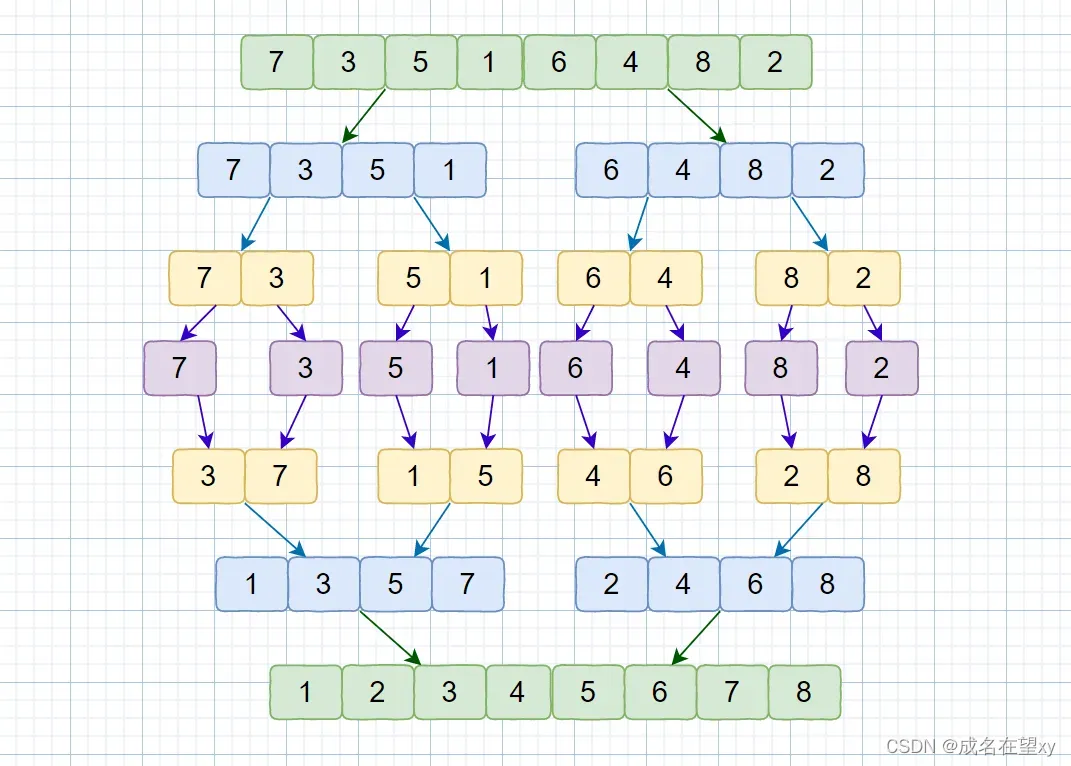
归并排序的一般策略是:开始时将表划分为大致相等的两段,然后对每个子表再递归调用,直到将表划分为很多个只含有一个元素的自然有序的子表。然后控制返回递归调用结构将每两个有序子表合并成一个表,直到所有子表合并成一个最终的有序表。
public static void mergeSort(Comparable[] data, int min, int max)
{
if (min < max)
{
int mid = (min + max)/2;
mergeSort(data, min, mid);
mergeSort(data, mid+1, max);
merge(data,min,mid,max);
}
}
public static void merge(Comparable[] data, int first, int mid, int last)
{
Comparable[] temp = new Comparable[data,length];
int first1 = first, last1 = mid;
int first2 = mid+1, last2 = last;
int index = first1;
while (first1 <= last1 && first2 <= last2)
{
if (data[first1].compareTo(data[first2]) < 0)
{
temp[index] = data[first1];
first1++;
}
else
{
temp[index] = data[first2];
first2++;
}
index++
}
while (first1 <= last1)
{
temp[index] = data[first1];
first1++;
index++;
}
while (first2 <= last2)
{
temp[index] = data[first2];
first2++;
index++;
}
for (index = first;index <= last; index++)
data[index] = temp[index];
}
mergeSort方法判定待排序表的中间点,然后两次递归调用,对二分的两段进行排序。当表的长度小于等于1时,通过if语句终止递归。从递归返回后,通过merge方法合并两个有序的子表,直到合并为完整的有序表。
merge方法接收三个整数,它们定义了数组中的两个有序子表。从下标first到mid的值是一个有序表,而从下标mid+1到下标last的值是另一个有序表。merge方法的任务就是将它们合并成一个有序表。方法中的第一个while循环扫描两个子表,将两个子表中的较小者放到temp数组中,持续这个过程直到所有的值都复制到temp数组中(因为都是有序表,所以一个子表转移完了的化就直接把另一个子表的剩余元素移到temp数组中)。最后的for循环将temp数组中的所有数据复制回原来的数组中。
排序算法的分析与比较
虽然选择排序、插入排序和冒泡排序使用不同的技术来解决问题,但它们都有相近的效率。这三种排序算法都使用一个嵌套另一个的双重循环来排列元素的次序,所以都有O(n2)的时间复杂度。
例如,选择排序的外层循环要迭代n-1次。对于外层循环的每次迭代,内层循环都对数组中的一部分元素进行重复操作(具体个数依赖于外层循环的哪次迭代,但总是小于n的)。所以每次内层迭代中都是常数级的操作。该算法的增长函数为:
f(n) = (n-1) * (一个常数*n + 另一个常数) = an2 + bn +c
考虑每种算法的最优及最差情形。对于选择和冒泡排序,处理过程基本上不依赖于待排序数据的初始排列。根据数据的不同,其元素交换的个数差别很小,因此它们的算法最优、最差及平均情形都是O(n2)。
而插入排序则会依赖于初始数据的情况。当初始数据呈逆序时,插入排序出现最差情形,此时内层循环要全部执行,基本上与平均情形相同,都为O(n2)。但是如果数组已经按正确次序排列,那么插入排序的内层循环只进行一次比较,所以插入排序的最优情形是O(n)。其实在部分有序的情况下,插入排序的运行速度也会很快。
考虑效率更高的快速排序算法。理想情况下,每次选中的划分元素将元素分为较大和较小的两部分,这样每次递归调用时都只对当前数据中大约一半的元素进行操作。在这种情况下,递归有log2(n)层。每一层中元素的划分都需要对数据进行一趟扫描,所以对一层的划分需要O(n),因此整个排序过程的时间复杂度是O(n log n)。
快速排序的最差情形时间复杂度是O(n^2)。
快速排序的关键是选择一个好的划分元素。在我上面代码的实现中,只是简单地选择了每段中的第一个元素。如果数组中的初始数据是随机的,那选择这个值和特意在段中选择一个值也没什么区别。我们能想到的一个好的划分元素的改进方法是:随机选择三个值,使用这三个值的中间值作为划分元素。
归并排序的分析与快速排序类似,特殊之处在于它可以保证每次递归分解总能将数据分成两半,所以它的层数就是log2(n)。归并部分需要对数据扫描一遍从而将两个子表归并起来,归并一层时需要O(n)。所以归并排序的最优最差及平均情形的算法复杂度都是O(n log n)。
归并算法的不足是需要临时数据空间来完成归并操作。一般情况下,确保能节省出来的运行时间优势可以抵消这个空间开销。但我们在快速排序和归并排序之间需要权衡——快速排序不占用额外的空间,但如果划分元素选择不好可能会降低它的效率;而归并排序能保证效率但是使用了额外的空间。