目录
前言
本次实验通过参考教材《Python计算机视觉编程》和网上大量资料学习局部图像描述子，Harris角点检测器，SIFT特征，匹配地理标记图像相关内容。
一、Harris角点检测算法
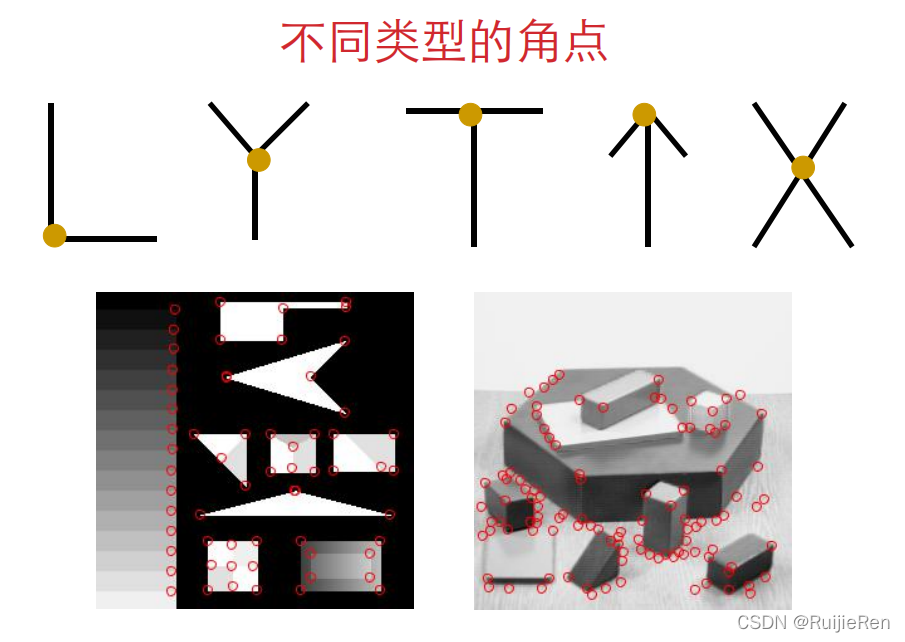
1.1 角点是什么
角点具有的特征：
<1>轮廓之间的交点；
<2>局部窗口沿任意方向移动，均产生明显变化的点；
<3>图像局部曲率突变的点；
<4>对于同一场景，即使视角发生变化，通常具备稳定性质的特征；
<5>该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化。
1.2 好的角点检测算法具备的特征
<1>检测出图像中“真实的”角点；
<2>准确的定位性能；
<3>具有很高的稳定性；
<4>具有对噪声的鲁棒性；
<5>具有较高的计算效率。
1.3 角点检测算法基本原理
基本原理：
人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，如果滑动前后窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了角点；如果滑动前后窗口内区域的灰度没有发生变化那么窗口内就不存在角点。
1.4 用数学方法刻画角点特征
首先，将图像窗口平移[u,v]产生灰度变化的自相关函数如下：
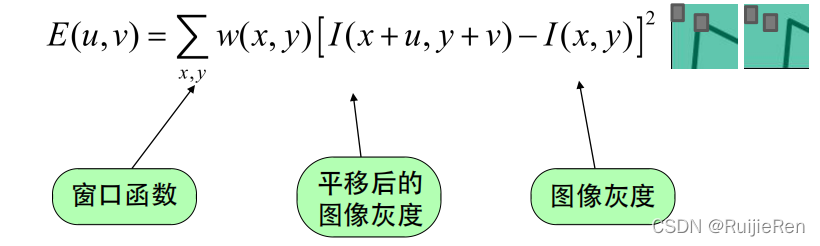
其中窗口函数（权重矩阵）可以是平坦的，也可以是高斯的如下图（权重矩阵W（通常为高斯滤波器Gσ）：
然后将I(x+u，y+v)函数在（x,y）处泰勒展开得：
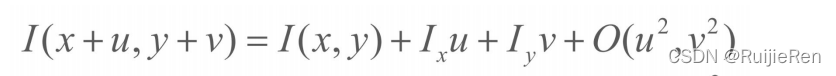
则：
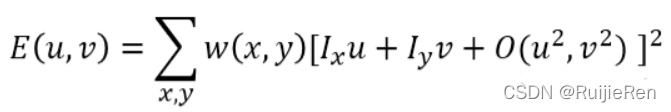
其中Ο(u2,v2)近似为0， 由于是对局部微小的移动量 [u,v]，所以可以近似得到下面忽略余项之后的表达式为一个二项式函数：
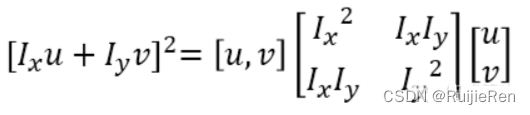
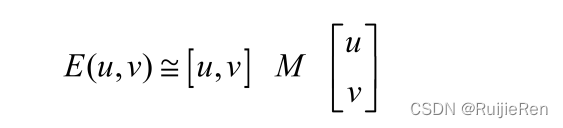
其中M是2X2矩阵，可由图像得导数求得：
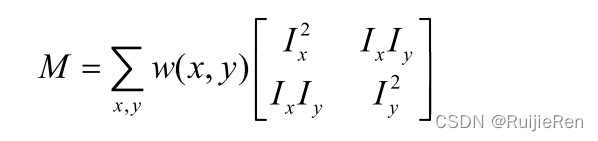
忽略余项之后的表达式为一个二项式函数，然而二项式函数的本质上就是一个椭圆函数，椭圆的扁率和尺寸是由M(x,y)的特征值λ1、λ2决定的，
椭圆的方向是由M(x,y)的特征矢量决定的，如下图所示，椭圆方程为：
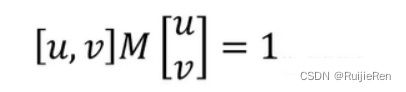
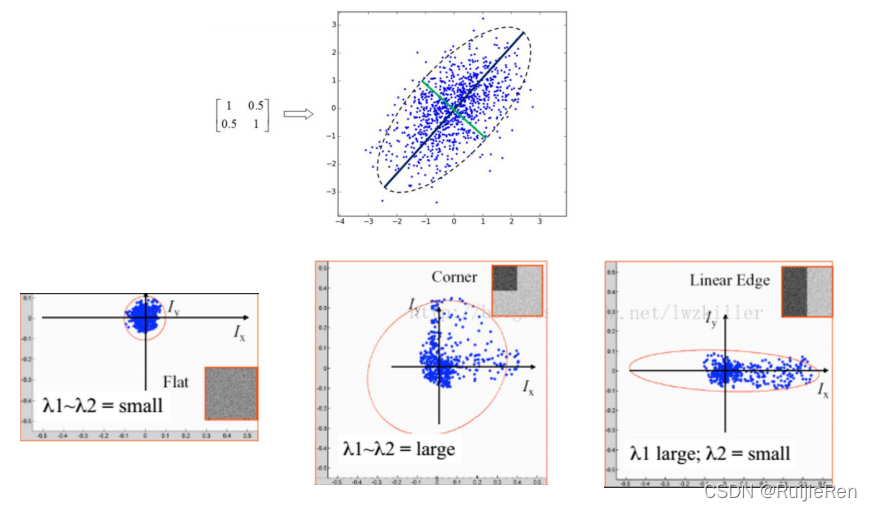
椭圆函数特征值与图像中的角点、直线（边缘）和平面之间的关系如下图所示。共可分为三种情况：
（1） 图像中的直线：一个特征值大，另一个特征值小，λ1>λ2或λ2>λ1。自相关函数值在某一方向上大，在其他方向上小。
（2）图像中的平面：两个特征值都小，且近似相等；自相关函数数值在各个方向上都小。
（3）图像中的角点：两个特征值都大，且近似相等，自相关函数在所有方向都增大。
通过M的两个特征值λ1和λ2的大小对图像点进行分类：
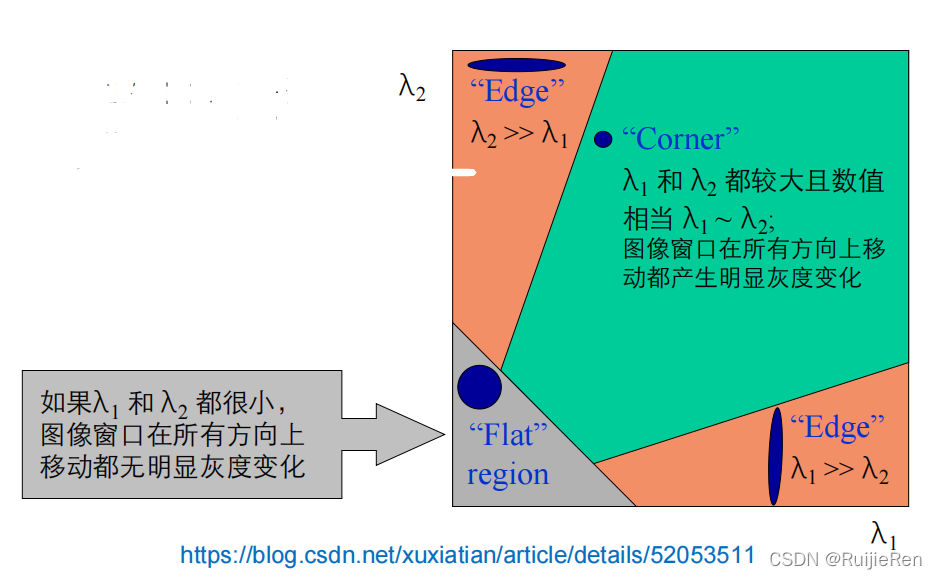
1.5 定义角点响应函数
由于我们是通过M的两个特征值的大小对图像进行分类，所以，定义角点相应函数R：
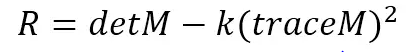
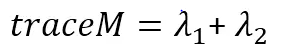
其中k为经验常数，一般取k=0.04~0.06。增大k的值将减小响应值R，降低检测的灵敏性，减少被检测角点的数量；减小k值，将增大角点响应值R，增加被检测角点的数量。为了去除加权常数κ，我们通常使用商数detM/(traceM)2作为指示器。所以，上图可以转化为：
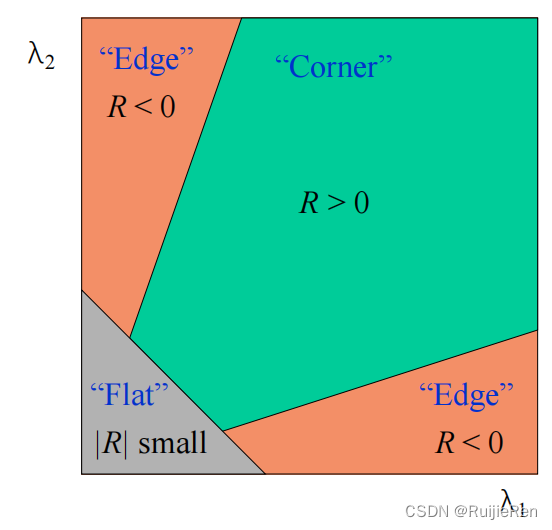
其中：
• R 只与M的特征值有关
• 角点：R 为大数值正数（λ1和λ2都是很大的正数）
• 边缘：R 为大数值负数
• 平坦区：R 为小数值（如果λ1≈λ2≈0，该区域为空）
在判断角点的时候，对角点响应函数R进行阈值处理：R > threshold，提取R的局部极大值。
1.6 Harris角点检测步骤
Harris角点检测可以分为5个步骤：
（1）计算图像I(x,y)I(x,y)在xx和yy两个方向的梯度IxIx,IyIy;
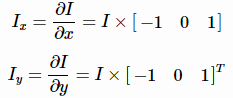
（2）计算图像两个方向梯度的乘积;
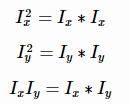
（3）使用高斯函数对Ix2、Iy2、IxIy进行高斯加权(取σ=2,ksize=3)，计算中心点为(x,y)(x,y)的窗口W对应的矩阵M；
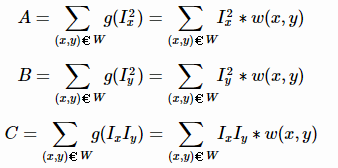
（4）计算每个像素点(x,y)处的(x,y)处的Harris响应值R；
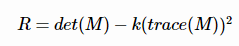
（5）过滤大于某一阈值t的R值；
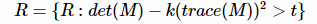
1.7 Harris角点检测算法的响应函数
Harris角点检测器的响应函数会返回像素值为 Harris 响应函数值的一幅图像。
代码展示：
# 角点响应函数
import numpy as np
from scipy.ndimage import filters
# 返回像素值为Harris响应函数值得一幅图像
def compute_harris_response(im, sigma=3):
""" 在一幅灰度图像中，对每个像素计算Harris角点检测器响应函数 """
# 计算导数
imx = np.zeros(im.shape)
filters.gaussian_filter(im,(sigma,sigma),(0,1),imx)
imy = np.zeros(im.shape)
filters.gaussian_filter(im,(sigma,sigma),(1,0),imy)
# 计算Harris矩阵的分量
Wxx = filters.gaussian_filter(imx*imx,sigma)
Wxy = filters.gaussian_filter(imx*imy,sigma)
Wyy = filters.gaussian_filter(imy*imy,sigma)
# 计算特征值和迹
Wdet = Wxx * Wyy - Wxy**2
Wtr = Wxx + Wyy
return Wdet / Wtr得到像素值为Harris响应函数值的图像后，我们需要从这幅图像中挑选出需要的信息，然后选取像素值高于阈值的所有图像点；再加上额外的限制，即角点之间的间隔必须大于设定的最小距离。这种方式会产生很好的角点检测结果。为了实现该算法，我们获取所有的候选像素点，以角点响应值递减的顺序排序，然后将距离已标记为角点位置过近的区域从候选像素点中删除。代码如下：
def get_harris_points(harrisim, min_dist=10, threshold=0.1):
"""从一幅Harris响应图像中返回角点。min_dist为分割角点和图像边界的最少像素数目"""
# 寻找高于阈值的候选角点
corner_threshold = harrisim.max() * threshold
harrisim_t = (harrisim > corner_threshold) * 1
# 得到候选角点的坐标
coords = np.array(harrisim_t.nonzero()).T
# 以及他们的Harris响应值
candidate_values = [harrisim[c[0], c[1]] for c in coords]
# 对候选点按照Harris响应值进行排序
index = np.argsort(candidate_values)
# 将可行点的位置保存到数组中
allowed_locations = np.zeros(harrisim.shape)
allowed_locations[min_dist:-min_dist, min_dist:-min_dist] = 1
# 按照min_distance原则，选择最佳Harris角点
filtered_coords = []
for i in index:
if allowed_locations[coords[i:0], coords[i, 1]] == 1:
filtered_coords.append(coords[i])
allowed_locations[(coords[i, 0] - min_dist):(coords[i, 0] + min_dist),
(coords[i, 1] - min_dist):(coords[i, 1] + min_dist)] = 0
return filtered_coords
1.8 Harris角点检测实例
测试不同阈值下的检测结果，代码如下：
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from Localdescriptors import harris
# 读入图像
img = np.array(Image.open('../image/JMU_5.jpg').convert('L'))
# 检测Harris角点
harrisim = harris.compute_harris_response(img)
# Harris响应函数
harrisim1 = 255 - harrisim
# print(harrisim1)
# 使其标题可以显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure()
plt.gray()
plt.subplot(141)
plt.imshow(harrisim1)
plt.title('harris响应函数值图像')
plt.axis('off')
filtered_coords1 = harris.get_harris_points(harrisim, 6, 0.01)
filtered_coords2 = harris.get_harris_points(harrisim, 6, 0.05)
filtered_coords3 = harris.get_harris_points(harrisim, 6, 0.1)
plt.subplot(142)
harris.plot_harris_points(img,filtered_coords1)
plt.title('阈值为0.01')
plt.subplot(143)
harris.plot_harris_points(img, filtered_coords2)
plt.title('阈值为0.05')
plt.subplot(144)
harris.plot_harris_points(img, filtered_coords3)
plt.title('阈值为0.1')
plt.show()
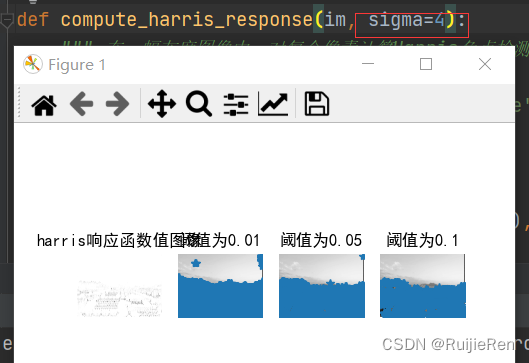
检测结果：
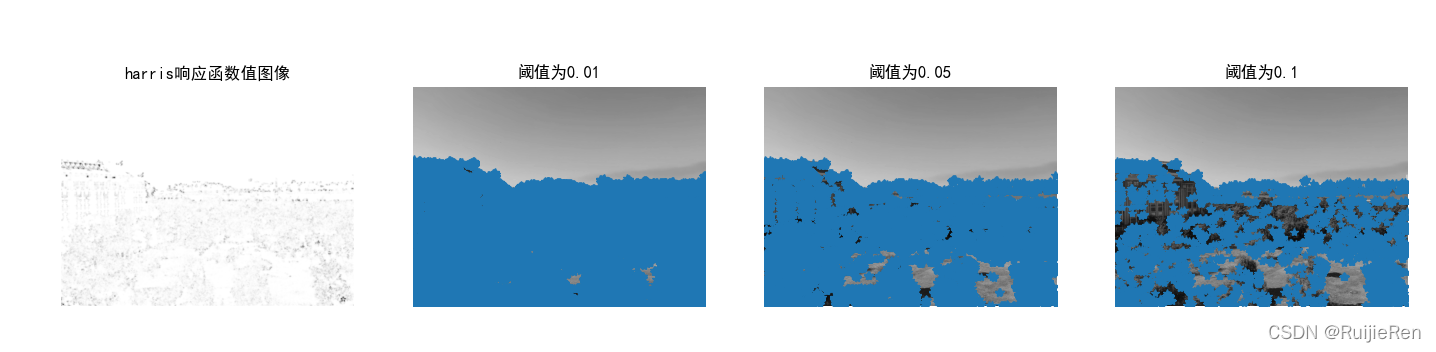
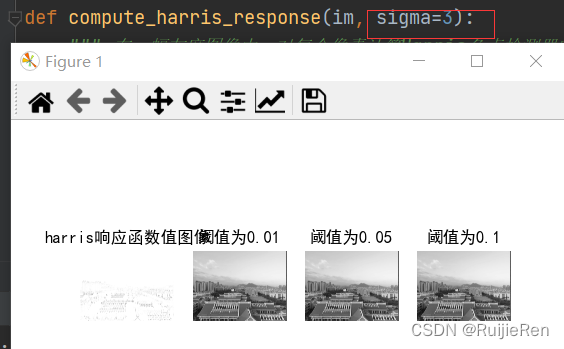
从结果来看， 在进行角点检测时，随着阈值变大，能被检测到的角点会相应的减少。同时在检测是还发现有些图片无法检测出角点，如下图：
通过多次改变参数，发现在高斯滤波器中参数sigma=3时无结果显示，增大sigma后有结果出现。
（具体原因还没搞懂）
1.9 不同场景下测试Harris角点检测器
1.9.1 角点丰富场景
将桌子上的课本，盒子，明信片堆在一起拍的四张照片，分别是近景、远景、光线较亮、光线较暗，测试在sigma = 3,阈值分别为0.01，0.05，0.1下的角点检测情况：
近景：
远景：
光线较亮：
光线较暗：
结果分析： 从以上结果对比来，四种情况均有角点被识别出来，近景比远景的角点要少，因为远景图像在检测出前景物体角点的同时也检测出一些周围背景的角点；而且可以明显看到光纤较亮的图像要比光线较暗的图像检测出更多角点，可以认为由于拍摄角度的偏差光线的亮暗对角点检测有影响。
1.9.2 纹理平坦场景
该场景选取一个平坦背景，从近景、远景、光线较亮、光线较暗四个角度测试角点检测情况：
近景：
远景:
光线较亮：
光线较暗：
在光线较暗时没有角点被检测出来，增大sigma = 5进行测试时有角点出现：
结果分析：在该场景下，平坦背景上几乎没有角点，远景由于背景范围较大，被检测出的角点也最多，但就中心前景而言两者角点数量差别不大，在光线较暗时如果sigma太小则无法检测出角点。从以上场景对比来看，Harris角点具有旋转不变性，平坦的界面相对于角点丰富的图像也更有利于角点的检测，高斯滤波器的尺度对角点检测有较大影响（参数sigma），Harris角点检测的最大缺点是对尺度很敏感，不具备尺度不变性。
1.10 图像种寻找对应点
Harris 角点检测器仅仅能够检测出图像中的兴趣点，但是没有给出通过比较图像间的兴趣点来寻找匹配角点的方法。我们需要在每个点上加入描述子信息，并给出一 个比较这些描述子的方法。兴趣点描述子是分配给兴趣点的一个向量，描述该点附近的图像的表观信息。描述子越好，寻找到的对应点越好。我们用对应点或者点的对应来描述相同物体和场景点在不同图像上形成的像素点。使用归一化的互相关矩阵进行两幅图像的比较，代码如下：
def get_descriptors(image,filtered_coords,wid=5):
"""对于每个返回的点，返回点周围2*wid+1个像素的值（假设选取点的min_distance > wid）"""
desc = []
for coords in filtered_coords:
patch = image[coords[0] - wid:coords[0]+wid+1,coords[1]-wid:coords[1]+wid+1].flatten()
desc.append(patch)
return desc
def match(desc1,desc2,threshold=0.5):
"""对于第一幅图像中的每个角点描述子，使用归一化互相关，选取它在第二幅图像中的匹配角点"""
n = len(desc1[0])
# 点对的距离
d = -np.ones((len(desc1), len(desc2)))
for i in range(len(desc1)):
for j in range(len(desc2)):
# mean:求平均值，std:求标准差
d1 = (desc1[i] - np.mean(desc1[i])) / np.std(desc1[i])
d2 = (desc2[j] - np.mean(desc2[j])) / np.std(desc2[j])
ncc_value = sum(d1 * d2) / (n-1)
if ncc_value > threshold: # 数值较高的距离代表两个点
d[i,j] = ncc_value
# np.argsort():将数组中的元素从小到大排列，提取其对应的index(索引)，然后输出
# 数值较高的距离代表两个点能够更好的匹配，因此对距离取相反数
ndx = np.argsort(-d)
matchscores = ndx[:0]
return matchscores
# 从第二幅图像向第一幅图像匹配，然后过滤掉在两种方法种不都是最好的匹配
def match_twosided(desc1,desc2,threshold=0.5):
"""两边对称版本的match()"""
matches_12 = match(desc1,desc2,threshold)
matches_21 = match(desc2,desc1,threshold)
# np.where:找到n维数组中特定数值的索引
ndx_12 = np.where(matches_12 >= 0)[0]
for n in ndx_12:
if matches_21[matches_12[n]] != n:
matches_12[n] = -1
return matches_12
# 实现匹配点的可视化
def appendimages(im1,im2):
"""返回将两幅图像并排拼接成一幅图像"""
# 选取具有最少行数的图像，然后填充足够的空行
rows1 = im1.shape[0]
rows2 = im2.shape[0]
if rows1 < rows2:
im1 = np.concatenate((im1, np.zeros((rows2 - rows1, im1.shape[1]))), axis=0)
elif rows1 > rows2:
im2 = np.concatenate((im2, np.zeros((rows1 - rows2, im2.shape[1]))), axis=0)
# 如果无此两种情况，则他们行数相同，无需填充
return np.concatenate((im1,im2),axis=1)
def plot_matches(im1,im2,locs1,locs2,matchscores,show_below=True):
"""显示一幅带有连接匹配之间连线的图片"""
"""
im1,im2:数组图像，locs1.locs2:特征位置，matchscores(match())的输出，
show_below(如果图像应该显示在匹配的下方)
"""
im3 = appendimages(im1,im2)
if show_below:
im3 = np.vstack((im3, im3))
plt.imshow(im3)
cols1 = im1.shape[1]
for i,m in enumerate(matchscores):
if m>0:
plt.plot([locs1[i][1],locs2[m][1]+cols1],[locs1[i][0],locs2[m][0]],'c')
plt.axis('off')
测试代码：
# -*- coding: utf-8 -*-
"""
@author: RRJ
@software: PyCharm
@file: harrisdemo3.py
@time: 2022/3/27 15:19
"""
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from Localdescriptors import harris
from tools.imtools import imresize
# 读入图像
im1 = np.array(Image.open("../JMU_img/JMU_ZS1.jpg").convert("L"))
im2 = np.array(Image.open("../JMU_img/JMU_ZS2.jpg").convert("L"))
# resize加快匹配速度
im1 = imresize(im1, (im1.shape[1]//2, im1.shape[0]//2))
im2 = imresize(im2, (im2.shape[1]//2, im2.shape[0]//2))
wid = 5
harrisim = harris.compute_harris_response(im1, 5)
filtered_coords1 = harris.get_harris_points(harrisim, wid+1)
d1 = harris.get_descriptors(im1, filtered_coords1, wid)
harrisim = harris.compute_harris_response(im2, 5)
filtered_coords2 = harris.get_harris_points(harrisim, wid+1)
d2 = harris.get_descriptors(im2, filtered_coords2, wid)
print('starting matching')
matches = harris.match_twosided(d1, d2)
plt.figure()
plt.gray()
harris.plot_matches(im1, im2, filtered_coords1, filtered_coords2, matches)
plt.show()
结果展示：
结果分析：从以上结果可以看到，虽然大部分点进行了匹配，但是有相当大一部分存在不正确匹配，尤其是在两幅图像拍摄角度偏差过大的时候，直接将左边的树枝点匹配到了右边，因此这种匹配方式适合目标图像拍摄角度差异不大的时候进行对应点匹配。同时在测试中发现效率较低，在图像尺寸稍大时运行速度极低。
二、SIFT（尺度不变特征变换）
2.1 SIFT简介
SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），是用于图像处理领域的一种描述。这种描述具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。SIFT特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。
2.2 SIFT特点
1.SIFT特征是图像的局部特征，其对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性；
2. 区分性好，信息量丰富，适用于在海量特征数据库中进行快速、准确的匹配；
3. 多量性，即使少数的几个物体也可以产生大量的SIFT特征向量；
4.高速性，经优化的SIFT匹配算法甚至可以达到实时的要求；
5.可扩展性，可以很方便的与其他形式的特征向量进行联合。
2.3 SIFT算法
2.3.1 SIFT算法可以解决的问题
（1）目标的旋转、缩放、平移；
（2）图像仿射或投影变换；
（3）弱光照影响以及部分目标遮挡；
（4）杂物场景以及噪声点影响。
2.3.2 SIFT算法实现特征匹配的三个流程：
1.提取关键点；
2.对关键点附加详细的信息（局部特征），即描述符；
3.通过特征点（附带上特征向量的关键点）的两两比较找出相互匹配的若干对特征点，建立景物间的对应关系。
2.3.3 SIFT中要查找的特征点
这些点是一些十分突出的点，不会因光照、尺度、旋转等因素的改变而消失，比如角点、边缘点、暗区域的亮点以及亮区域的暗点。假定两幅图像中有相同的景物，那么使用某种算法分别提取各自的特征点，这些点之间会有相互对应匹配关系。根据归纳，我们可以看出SIFT特征点希望选出具有下述不变性的点：尺度、方向、位移、光照
2.4 尺度空间
在一定的范围内，无论物体是大还是小，人眼都可以分辨出来。然而计算机要有相同的能力却不是那么的容易，在未知的场景中，计算机视觉并不能提供物体的尺度大小，其中的一种方法是把物体不同尺度下的图像都提供给机器，让机器能够对物体在不同的尺度下有一个统一的认知。在建立统一认知的过程中，要考虑的就是在图像在不同的尺度下都存在的特征点。
而尺度空间的基本思想是：在图像信息处理模型中引入一个被视为尺度的参数，通过连续变化尺度参数获得多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点检测和不同分辨率上的特征提取等。尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。要使得图像具有尺度空间不变性，就要建立尺度空间。
一个图像的尺度空间，定义为一个变化尺度的高斯函数
与原图像
的卷积。
其中*表示卷积运算，(x, y)代表图像的像素位置，尺度空间因子，值越小表示图像被平滑的越少，相应的尺度也就越小。大尺度对应于图像的概貌特征，小尺度对应于图像的细节特征。
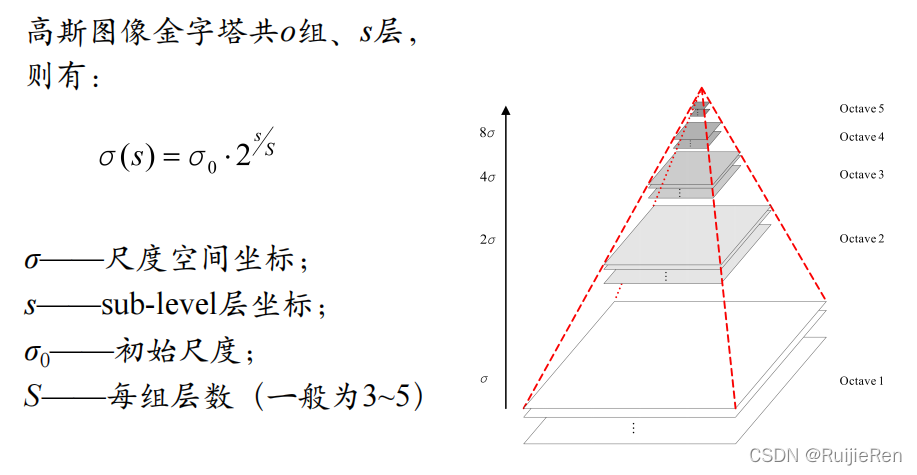
2.5 高斯金字塔
尺度空间在实现时使用高斯金字塔表示，高斯金字塔的构建分为两部分：
（1）对图像做不同尺度的高斯模糊；
（2）对图像做降采样(隔点采样)
图像的金字塔模型是指，将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，从下到上构成的塔状模型。原图像为金字塔的第一层，每次降采样所得到的新图像为金字塔的一层(每层一张图像)，每个金字塔的具体层数根据图像的原始大小和塔顶图像的大小共同决定。为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波。如图所示，将图像金字塔每层的一张图像使用不同参数做高斯模糊。
2.6 关键点检测-DOG
2.6.1 DOG函数（高斯差分函数）
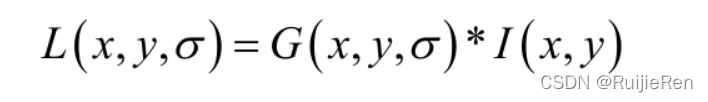
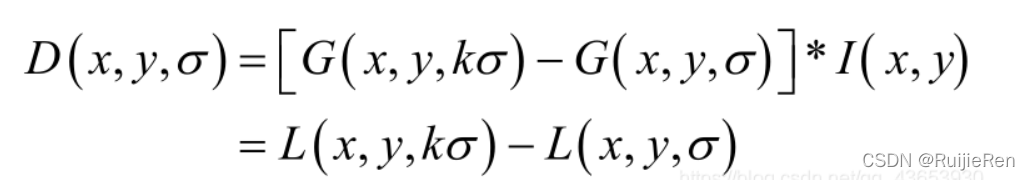
2.6.2 DoG高斯差分金字塔
（1）对应DOG算子，构建DOG金字塔。
可通过高斯差分图像看出图像上的像素值变化情况(如果没有变化也就没有特征，特征必须是变化尽可能多的点)，DOG图像描绘的是目标的轮廓。
（2）DOG局部极值检测
特征点是由DOG空间的局部极值点组成的。为了寻找DoG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小，看其是否比它的图像域和尺度域的相邻点大或者小。如下图所示，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。一个点如果在DOG尺度空间本层以及上下两层的26个领域中是最大或最小值时，就认为该点是图像在该尺度下的一个特征点。
（3）去除边缘效应
由于DOG函数在图像边缘有较强的边缘响应，因此需要排除边缘响应。DOG函数的峰值点在边缘梯度的方向上主曲率值比较大，而沿着边缘方向则主曲率值较小。
2.7 关键点方向分配、描述和匹配
2.7.1 关键点方向分配
为了使描述符具有旋转不变性，需要利用图像的局部特征为每一个关键点分配一个方向。通过尺度不变性求极值点，可以使其具有缩放不变的性质。而利用关键点邻域像素的梯度方向分布特性，可以为每个关键点指定参数方向，从而使描述子对图像旋转具有不变性。
通过求每个极值点的梯度来为极值点赋予方向，完成关键点的梯度计算后，使用直方图统计邻域内像素的梯度和方向。确定关键点的方向采用梯度直方图统计法，统计以关键点为原点，一定区域内的图像像素点对关键点方向生成所作的贡献。
2.7.2 关键点描述
经过一系列步骤此时对于每一个关键点都拥有三个信息：位置、尺度以及方向。然后就是为每个关键点建立一个描述符，用一组向量将这个关键点描述出来，使其不随各种变化而改变，比如光照和视角等变化。这个描述子不但包括关键点，也包含关键点周围对其有贡献的像素点，并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。
SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示。通过对关键点周围图像区域分块，计算块内梯度直方图，生成具有独特性的向量，这个向量对该区域图像信息的表达具有唯一性。
Lowe实验结果表明：描述子采用4×4×8＝128维向量表征，综合效果最优（不变性与独特性）。
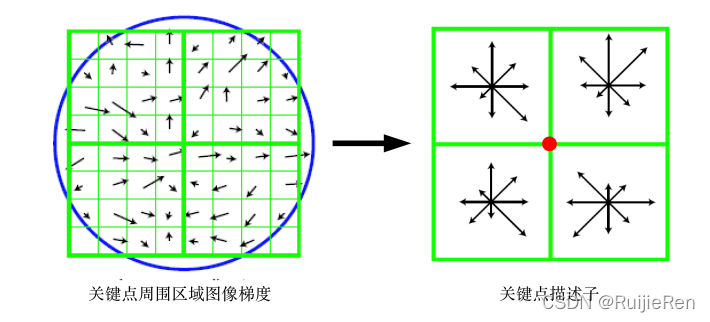
2.7.3 关键点匹配
（1）分别对模板图（参考图，reference image）和实时图（观测图，observation image）建立关
键点描述子集合。目标的识别是通过两点集内关键点描述子的比对来完成。具有128维的关键点描
述子的相似性度量采用欧式距离。
（2）关键点的匹配可以采用穷举法来完成，但是这样耗费的时间太多，一般都采用kd树的数据结
构来完成搜索。搜索的内容是以目标图像的关键点为基准，搜索与目标图像的特征点最邻近的原图
像特征点和次邻近的原图像特征点。
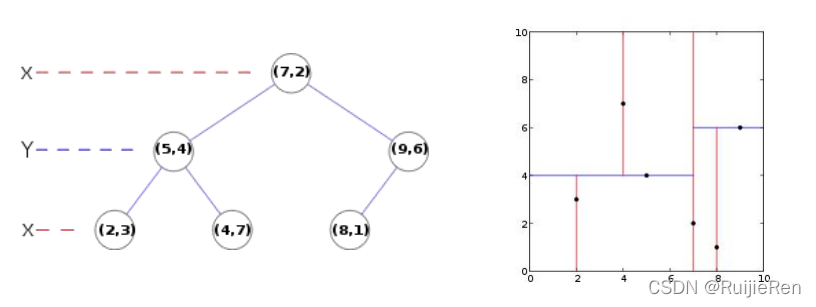
2.8 SIFT算法实现
2.8.1 SIFT特征检测
检测兴趣点我们使用开源工具宝VLFeat提供的二进制文件来计算图像的SIFT特征。VLfeat下载在VLfeat官网，安装可参考教程，建议安装vlfeat-0.9.20-bin.tar.gz版本，因为在安装vlfeat-0.9.21-bin.tar.gz后有如下报错：百度说是VLfeat的版本过高的问题
由于该二进制文件需要的图像格式是灰度.pgm,所以如果图像为其他格式，我们需要首先将其转换成.pgm格式文件，转换的结果以易读的格式保存在文本文件中。转换代码如下：
def process_image(imagename, resultname, params="--edge-thresh 10 --peak-thresh 5"):
""" 处理一幅图像，然后将结果保存在文件中"""
if imagename[-3:] != 'pgm':
# create a pgm file
im = Image.open(imagename).convert('L')
im.save('tmp.pgm')
imagename = 'tmp.pgm'
cmmd = str("D:\python\win64VLfeat\sift.exe " + imagename + " --output=" + resultname +
" " + params)
os.system(cmmd)
print('processed', imagename, 'to', resultname)转换的结果以易读的格式保存在文本文件中，文本文件如下：
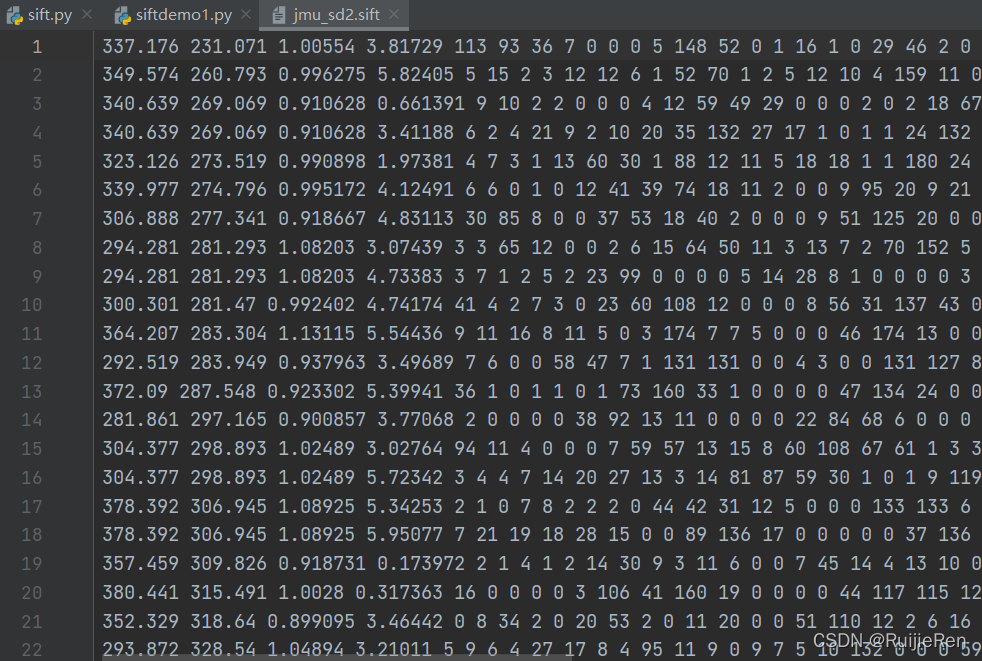
上面数据的每一行前4个数值依次表示兴趣点的坐标、尺度和方向角度，后面紧接着的是对应描述符的128维向量。
下面是从文本文件中将特征读取到NumPy数组中的函数：
def read_features_from_file(filename):
""" 读取特征属性值，然后将其以矩阵的形式返回"""
f = np.loadtxt(filename)
return f[:, :4], f[:, 4:] # 特征位置，描述子读取特征后，通过在图像上绘制他们的位置，将其可视化，绘制图像函数如下：
def plot_features(im,locs,circle=False):
"""显示带有特征的图像"""
"""输入：im(数组图像),locs(每个特征的行、列、尺度和方向角度)"""
def draw_circle(c,r):
"""绘制圆圈,圆圈的半径为特征的尺度"""
t = np.arange(0,1.01,.01) * 2 * np.pi
x = r * np.cos(t) + c[0]
y = r * np.sin(t) + c[1]
plt.plot(x,y,'b',linewidth=2)
plt.imshow(im)
if circle:
for p in locs:
draw_circle(p[:2],p[2])
else:
# 在原始图像上用蓝色圆圈绘制SIFT特征点位置
plt.plot(locs[:,0],locs[:,1],'ob')
plt.axis('off')
测试代码：
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
from Localdescriptors import sift
from Localdescriptors import harris
# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc", size=14)
imname = '../JMU_img/JMU_SD2.png'
# 以灰度图的方式读入图片
im = np.array(Image.open(imname).convert('L'))
# 引用sift.py中的process_image将图像文件转化为pgm格式
sift.process_image(imname, 'jmu_sd2.sift')
# l1为兴趣点坐标、尺度和方位角度,d1是对应描述符的128 维向量
l1, d1 = sift.read_features_from_file('jmu_sd2.sift')
plt.figure()
plt.gray()
plt.subplot(221)
plt.imshow(im,cmap='gray')
plt.axis('off')
plt.title(u'原图像',fontproperties=font)
plt.subplot(222)
# 检测Harris角点
harrisim = harris.compute_harris_response(im)
filtered_coords = harris.get_harris_points(harrisim, 6, 0.05)
harris.plot_harris_points(im, filtered_coords)
plt.title(u'阈值为0.05的Harris角点',fontproperties=font)
plt.subplot(223)
sift.plot_features(im, l1, circle=False)
plt.title(u'SIFT特征',fontproperties=font)
plt.subplot(224)
sift.plot_features(im, l1, circle=True)
plt.title(u'圆圈表示特征尺度的SIFT特征',fontproperties=font)
plt.show()
结果展示：
结果分析：Harris和SIFT检测出的特征基本一致，但是SIFT提取出的特征更多，SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等，在图上可以看到SIFT检测出了草坪上的一些特征点，而Harris方法检测到的很少。
2.8.2 SIFT特征匹配
对于将一幅图像中的特征匹配到另一幅图像的特征，一种稳健的准则是使用这两个特征距离和两个最匹配特征的比率。相比于图像中的其他特征，该准则保证能够找到足够相似的唯一特征。使用该方法可以使错误的匹配数降低。匹配函数如下：
def match(desc1, desc2):
""" 对于第一幅图像中的每个描述子，选取其在第二幅图像中的匹配
输入：desc1(第一幅图像中的描述子)，desc2(第二幅图像中的描述子)
"""
desc1 = np.array([d / np.linalg.norm(d) for d in desc1])
desc2 = np.array([d / np.linalg.norm(d) for d in desc2])
dist_ratio = 0.6
desc1_size = desc1.shape
matchscores = np.zeros((desc1_size[0]), 'int')
desc2t = desc2.T # 预先计算矩阵转置
for i in range(desc1_size[0]):
dotprods = np.dot(desc1[i, :], desc2t) # 向量点乘
dotprods = 0.9999 * dotprods
# 反余弦和反排序，返回第二幅图像中特征的索引
indx = np.argsort(np.arccos(dotprods))
# 检查最近邻的角度是否小于dist_ratio乘以第二近邻的角度
if np.arccos(dotprods)[indx[0]] < dist_ratio * np.arccos(dotprods)[indx[1]]:
matchscores[i] = int(indx[0])
return matchscores
该函数使用描述子向量间的夹角作为距离度量。为了进一步增加匹配的稳健性，我们可以再反过来执行依次该步骤，用另外的方法匹配（从第二幅图像中的特征向第一幅图像中的特征匹配）。最后仅保留同时满足这两种匹配准则的对应。代码如下：
def match_twosided(desc1, desc2):
""" 双向对称版本的 match()"""
matches_12 = match(desc1, desc2)
matches_21 = match(desc2, desc1)
ndx_12 = matches_12.nonzero()[0]
# 去除不对称的匹配
for n in ndx_12:
if matches_21[int(matches_12[n])] != n:
matches_12[n] = 0
return matches_12实现匹配点的可视化：
# 实现匹配点的可视化
def appendimages(im1,im2):
"""返回将两幅图像并排拼接成一幅图像"""
# 选取具有最少行数的图像，然后填充足够的空行
rows1 = im1.shape[0]
rows2 = im2.shape[0]
if rows1 < rows2:
im1 = np.concatenate((im1, np.zeros((rows2 - rows1, im1.shape[1]))), axis=0)
elif rows1 > rows2:
im2 = np.concatenate((im2, np.zeros((rows1 - rows2, im2.shape[1]))), axis=0)
# 如果无此两种情况，则他们行数相同，无需填充
return np.concatenate((im1,im2),axis=1)
def plot_matches(im1,im2,locs1,locs2,matchscores,show_below=True):
"""显示一幅带有连接匹配之间连线的图片"""
"""
im1,im2:数组图像，locs1.locs2:特征位置，matchscores(match())的输出，
show_below(如果图像应该显示在匹配的下方)
"""
im3 = appendimages(im1,im2)
if show_below:
im3 = np.vstack((im3, im3))
plt.imshow(im3)
cols1 = im1.shape[1]
for i,m in enumerate(matchscores):
if m>0:
plt.plot([locs1[i][1],locs2[m][1]+cols1],[locs1[i][0],locs2[m][0]],'c')
plt.axis('off')测试代码：
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
import sys
from Localdescriptors import sift
# 添加中文字体支持
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"C:\Windows\Fonts\simsun.ttc",size=14)
im1path = '../JMU_img/JMU_ZS2.jpg'
im2path = '../JMU_img/JMU_ZS1.jpg'
im1 = np.array(Image.open(im1path))
im2 = np.array(Image.open(im2path))
sift.process_image(im1path, 'out_sift_ZS2.txt')
l1, d1 = sift.read_features_from_file('out_sift_ZS2.txt')
plt.figure()
plt.gray()
plt.subplot(121)
sift.plot_features(im1, l1, circle=False)
plt.title(u'第一幅图SIFT特征',fontproperties=font)
sift.process_image(im2path, 'out_sift_ZS1.txt')
l2, d2 = sift.read_features_from_file('out_sift_ZS1.txt')
plt.subplot(122)
sift.plot_features(im2, l2, circle=False)
plt.title(u'第二幅图SIFT特征',fontproperties=font)
# 输出两张图像的匹配度
matches = sift.match_twosided(d1, d2)
print('{} matches'.format(len(matches.nonzero()[0])))
plt.figure()
plt.gray()
sift.plot_matches(im1, im2, l1, l2, matches, show_below=True)
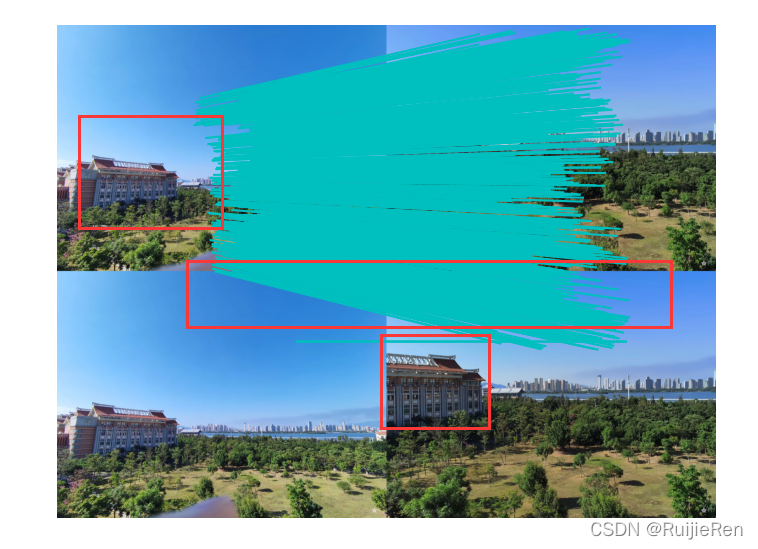
plt.show()展示结果：
SIFT特征： （第一组）
（第二组）
Harris:(第一组)
（第二组）
结果分析：两组图像的匹配结果对比，SIFT特征匹配相对更好一点，因为它有较高的运行效率，同时匹配的正确率也不错，但仍然有房屋建筑这种明显点没有得到匹配，同时对某一建筑物拍摄角度的要求会较高，SIFT在图像的不变特征提取方面拥有一定的优势，对角度差别较大的同一图像检测出的特征点过少。而Harris角点检测对对角度的要求较低，但是不存在尺度不变性，运行效率明显低于SIFT。总而言之，两种方法的选择 视情况而定，在用SIFT检测时，注意要用相同大小的图片，否则会报错无法运行，如下：
三、匹配地理标记图像
3.1 工具包安装
我们首先通过图像间是否具有匹配的局部描述子来定义图像间的连接，然后可视化这些连接情况。为了完成可视化，我们可以在图中显示这些图像，图的边代表连接。因此将使用pydot工具包和GraphViz图形库。安装顺序：graphviz--->graphviz软件包--->pydot。具体安装看：教程+Graphviz配置。
图像像素过大会导致运行时间很长，因此批量修改图像尺寸，代码如下：
from PIL import Image
import os.path
import glob
def convertjpg(jpgfile, outdir, width=640, height=480):
img = Image.open(jpgfile)
try:
new_img = img.resize((width, height), Image.BILINEAR)
new_img.save(os.path.join(outdir, os.path.basename(jpgfile)))
except Exception as e:
print(e)
for jpgfile in glob.glob("D:\\python\\RRJ\\pycharmproject\\jmu_image\\in_jmu\\*.jpg"):
convertjpg(jpgfile, "D:\\python\\RRJ\\pycharmproject\\jmu_image\\in2_jmu")
print('修改完成')
3.2 匹配地理标记图像代码：
# -*- coding: utf-8 -*-
"""
@author: RRJ
@software: PyCharm
@file: matchdemo1.py
@time: 2022/3/30 10:54
"""
# from pylab import *
import numpy as np
from PIL import Image
from Localdescriptors import sift
from tools import imtools
import pydot
# 将其设置为存储图像的路径
download_path = "D:\python\RRJ\pycharmproject\jmu_image\in2_jmu"
# 保存缩略图的路径（pydot需要完整的系统路径）
path = "D:\\python\\RRJ\\pycharmproject\\jmu_image\\out_jmu\\"
# 下载的文件名列表
imlist = imtools.get_imlist(download_path)
nbr_images = len(imlist)
# 提取特征
featlist = [imname[:-3] + 'sift' for imname in imlist]
for i, imname in enumerate(imlist):
sift.process_image(imname, featlist[i])
matchscores = np.zeros((nbr_images, nbr_images))
for i in range(nbr_images):
for j in range(i, nbr_images): # 仅仅计算上三角
print('comparing ', imlist[i], imlist[j])
l1, d1 = sift.read_features_from_file(featlist[i])
l2, d2 = sift.read_features_from_file(featlist[j])
matches = sift.match_twosided(d1, d2)
nbr_matches = sum(matches > 0)
print('number of matches = ', nbr_matches)
matchscores[i, j] = nbr_matches
print("The match scores is: \n", matchscores)
# 复制值
for i in range(nbr_images):
for j in range(i + 1, nbr_images): # 无需复制对角线
matchscores[j, i] = matchscores[i, j]
# 可视化
threshold = 2 # 创建关联所需的最小匹配数目
g = pydot.Dot(graph_type='graph') # 不使用默认的有向图
for i in range(nbr_images):
for j in range(i + 1, nbr_images):
if matchscores[i, j] > threshold:
# 图像对中的第一幅图像
im = Image.open(imlist[i])
im.thumbnail((100, 100))
filename = path + str(i) + '.png'
im.save(filename) # 需要大小合适的临时文件
g.add_node(pydot.Node(str(i), fontcolor='transparent', shape='rectangle', image=filename))
# 图像对中的第一幅图像
im = Image.open(imlist[j])
im.thumbnail((100, 100))
filename = path + str(j) + '.png'
im.save(filename) # 需要大小合适的临时文件
g.add_node(pydot.Node(str(j), fontcolor='transparent', shape='rectangle', image=filename))
g.add_edge(pydot.Edge(str(i), str(j)))
g.write_png('jmu1.png')
print('结束')
3.3 结果展示
原图像集：
匹配结果：
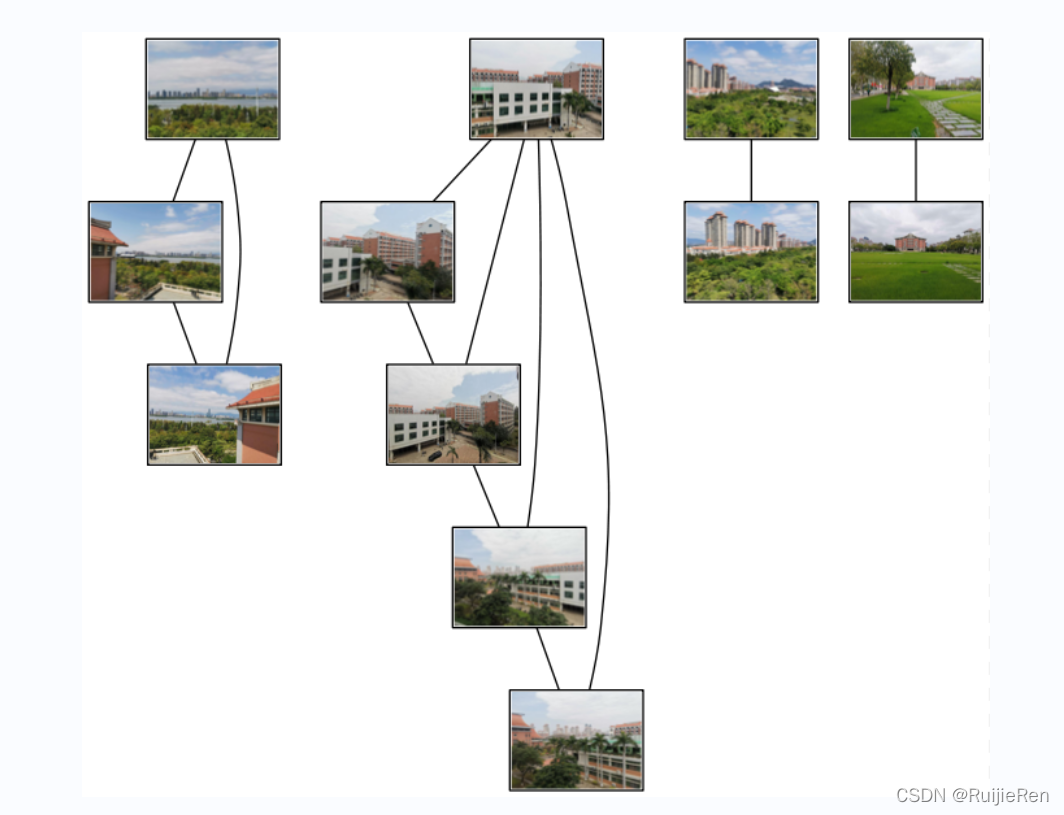
在原图像集中标出未匹配的图像：
结果分析：2.jpg和3.jpg是在不同角度、不同光线下拍的，通过人眼很明显看出两者有关联性，同样5.jpg和7.jpg也有明显特征建筑，但是匹配结果并未显示，猜测原因是由于拍摄角度偏差太大导致，1.jpg,16.jpg,4.jpg是同一大场景拍的三张，可以拼为一张完整的，结果也是得到了很好的匹配。通过测试发现图像拍摄角度对SIFT特征匹配有较大影响，数据集图片的大小对运行效率也有一定的影响，建议将图片尺寸修改为1000以内。
总结
本次实验测试了Harris角点检测与SIFT特征提取流程，对比了二者不同场景特征提取的准确性，过程中遇到很多问题，好在参考学姐学长博客解决及时完成作业。
参考资料：
（1）Harris角点检测原理 - 量子与太极 - 博客园 (cnblogs.com)
（2）《Python计算机视觉编程》及：(15条消息) python计算机视觉-图像处理基础章节之第二章 图像局部描述符_我超爱Debug的博客-CSDN博客（3）(16条消息) 计算机视觉3—SIFT理解与应用_w.wyue的博客-CSDN博客_sift应用