斐波那契数列类
LeetCode70. Climbing Stairs
题目描述:有 N 阶楼梯,每次可以上一阶或者两阶,求有多少种上楼梯的方法。
dp[ i ] = dp[ i-1 ] + dp[ i-2 ];
public int climbStairs(int n) {
if (n <= 2) {
return n;
}
int pre2 = 1, pre1 = 2;
for (int i = 2; i < n; i++) {
int cur = pre1 + pre2;
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
198, House Robber
抢劫一排住户,但是不能抢邻近的住户,求最大抢劫量。
dp[ i ] = max( dp[ i-1 ] , dp[ i-2 ] + arr[i])
public int rob(int[] nums) {
int pre2 = 0, pre1 = 0;
for (int i = 0; i < nums.length; i++) {
int cur = Math.max(pre2 + nums[i], pre1);
pre2 = pre1;
pre1 = cur;
}
return pre1;
}
213, House Robber II
强盗抢劫环形街道;
将数组分两种情况,一个是从nums[ o ~ n-2 ],另一个nums[ 1 ~ n-1 ],求最大
// LeetCode测试用例中会出现 [1,2] 而不是 [1,2,1],要注意
public class LeetCode213 {
public int rob(int[] nums) {
if(nums == null || nums.length == 0) return 0;
int ln = nums.length;
if(ln == 1) return nums[0];
return Math.max(max(nums, 0, ln-2), max(nums, 1, ln-1));
}
private int max(int[] nums, int start, int end) {
int pre1 = 0, pre2 = 0;
for(int i = start; i <= end; i++) {
int cur = Math.max(pre1+nums[i], pre2);
pre1 = pre2;
pre2 = cur;
}
return pre2;
}
}
信件错排
有 N 个 信 和 信封,它们被打乱,求错误装信方式的数量。
定义一个数组 dp 存储错误方式数量,dp[i] 表示前 i 个信和信封的错误方式数量。假设第 i 个信装到第 j 个信封里面,而第 j 个信装到第 k 个信封里面。根据 i 和 k 是否相等,有两种情况:
- i==k,交换 i 和 k 的信后,它们的信和信封在正确的位置,但是其余 i-2 封信有 dp[i-2] 种错误装信的方式。由于 j 有 i-1 种取值,因此共有 (i-1)*dp[i-2] 种错误装信方式。
- i != k,交换 i 和 j 的信后,第 i 个信和信封在正确的位置,其余 i-1 封信有 dp[i-1] 种错误装信方式。由于 j 有 i-1 种取值,因此共有 (i-1)*dp[i-1] 种错误装信方式。
综上所述,错误装信数量方式数量为:
dp[ i ] = ( i-1 ) * dp[ i-1 ] + ( i-1 ) * dp [ i-2 ]
母牛生产
程序员代码面试指南-P181
假设农场中成熟的母牛每年都会生 1 头小母牛,并且永远不会死。第一年有 1 只小母牛,从第二年开始,母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N,求 N 年后牛的数量。
dp[ i ] = dp[ i-3 ] + dp[ i -1 ];
矩阵路径类
64, Minimum Path Sum
矩阵的最小路径和;
dp[ i ][ j ] 表示matrix[i][j]位置的最小路径和
//采用辅助矩阵dp[][], 时间与空间复杂度都为O(M*N)
public int solve(int[][] matrix) {
int row = matrix.length;
int column = matrix[0].length;
int[][] dp = new int[row][column];
dp[0][0] = matrix[0][0];
for (int i = 1; i < column; i++) {
dp[0][i] = matrix[0][i] + dp[0][i-1];
}
for (int i = 1; i < row; i++) {
dp[i][0] = dp[i-1][0] + matrix[i][0];
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < column; j++) {
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + matrix[i][j];
}
}
return dp[row-1][column-1];
}
进行空间优化
//对方法进行改进,将空间复杂度压为O(min{M,N})
public int solveAdvan(int[][] matrix) {
int more = Math.max(matrix.length, matrix[0].length); //代表长的一边
int less = Math.min(matrix.length, matrix[0].length); //代表短的一边
int[] dp = new int[less];
boolean rowShorter = less == matrix.length;//是否行比列短
dp[0] = matrix[0][0];
for (int i = 1; i < less; i++) {
dp[i] = dp[i-1] + (rowShorter ? matrix[i][0] : matrix[0][i]);
}
for (int i = 1; i < more; i++) {
dp[0] += (rowShorter ? matrix[0][i] : matrix[i][0]);
for (int j = 1; j < less; j++) {
dp[j] = Math.min(dp[j-1], dp[j]) + matrix[i][j];
}
}
return dp[less-1];
}
62, Unique Paths
矩阵的总路径数:
public int uniquePaths(int m, int n) {
if (m < n) {
int temp = m;
m = n;
n = temp;
}
int[] dp = new int[n];
for (int i = 0; i < n; i++) {
dp[i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[j] = dp[j-1] + dp[j];
}
}
return dp[n-1];
}
也可以直接用数学公式求解,这是一个组合问题。机器人总共移动的次数 S=m+n-2,向下移动的次数 D=m-1,那么问题可以看成从 S 中取出 D 个位置的组合数量,这个问题的解为 C(S, D)。
数组区间
413, Arithmetic Slices
数组中等差递增子区间的个数
dp[i] 表示以 A[i] 为结尾的等差递增子区间的个数。
public int numberOfArithmeticSlices(int[] A) {
if(A == null || A.length == 0) return 0;
int n = A.length;
int[] dp = new int[n];
for(int i = 2; i < n; i++) {
if(A[i]-A[i-1] == A[i-1]-A[i-2]) dp[i] = dp[i-1]+1;
}
int total = 0;
for(int e: dp) total += e;
return total;
}
416.,分割等和子集
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
题目经分析后变为:数组总和sum必须为偶数,求数组是否含有和为sum/2的子序列。
解法一:动态规划
dp[ i ][ j ]的含义是:表示nums[0 - i-1]组成 J 值的可能性。
它的值为:
1)不包含 nums[i-1] : nums[ 0 ~ i-2 ]组成 J 的可能性,即dp[ i-1 ][ j ]。
2)包含 nums[ i-1 ] : j >= nums[i-1]的情况下,nums[ 0 ~ i-2 ]组成 j-nums[i-1] 的可能性,即dp[ i-1 ][ j-nums[i-1] ]
public boolean canPartition(int[] nums) {
if(nums == null) return false;
int sum = 0;
for(int num : nums) sum += num;
if((sum & 1) == 1) return false;
sum /= 2;
// dp[i][j]表示nums[0 - i-1]组成 j 值的可能性
boolean[][] dp = new boolean[nums.length+1][sum+1];
dp[0][0] = true;
for(int i = 1; i < dp.length; i++){
for(int j = 1; j < dp[0].length; j++){
dp[i][j] = dp[i-1][j];
if(j >= nums[i-1]){
dp[i][j] = dp[i][j] || dp[i-1][j-nums[i-1]];
}
}
}
return dp[nums.length][sum];
}
分析后可以进行空间压缩
public boolean canPartition2(int[] nums) {
if(nums == null) return false;
int sum = 0;
for(int num : nums) sum += num;
if((sum & 1) == 1) return false;
sum /= 2;
boolean[] dp = new boolean[sum+1];
dp[0] = true;
for(int num : nums){
for(int j = sum; j >= num; j--){
dp[j] = dp[j] || dp[j-nums[i-1]];
}
}
return dp[sum];
}
一开始分析题目时将问题转化后,可以看出,该题可以使用深度优先搜索的方式找出符合要求的序列。
public boolean canPartition3(int[] nums) {
if(nums == null) return false;
int sum = 0;
for(int num : nums) sum += num;
if((sum & 1) == 1) return false;
return recur(nums, sum/2, nums.length-1);
}
private boolean recur(int[] nums, int target, int index){
if(target == 0) return true;
if(index < 0 || target < 0) return false;
// 找出包含 nums[index] 在内的所有序列中是否有符合要求的
if(recur(nums, target-nums[index], index-1)) return true;
// 排除重复值
int j = index-1;
while (j >= 0 && nums[j] == nums[index]) j--;
// 抛弃nums[index]
return recur(nums, target, j);
}
分割整数
343, Integer Break
分割整数的最大乘积
public int integerBreak(int n) {
if (n < 2) return 0;
int[] dp = new int[n+1];
dp[1] = 1;
for(int i = 2; i <= n; i++) {
int max = 0;
for(int j = i-1; j >= (i+1)/2; j--) {
if (j < 4 && i-j < 4) max = Math.max(max, j*(i-j));
else if (j < 4) max = Math.max(max, j * dp[i-j]);
else if (i-j < 4) max = Math.max(max, dp[j]*(i-j));
else max = Math.max(max, dp[j]*dp[i-j]);
}
dp[i] = max;
}
return dp[n];
}
279.,Perfect Squares
按平方数来分割整数
public int numSquares(int n) {
int[] dp = new int[n+1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for(int i = 1; i <= n; i++) {
for(int j = 1; j*j <= i; j++) {
dp[i] = Math.min(dp[i], dp[i-j*j]+1);
}
}
return dp[n];
}
91,Decode Ways
分割整数构成字母字符串
dp[ i ] 代表 arr[ i ~ n-1 ] 构成字母字符串的可能个数,注意 0 ,若arr[ i ] = 0, 则dp[ i ] = 0;
public int numDecodings(String s) {
if (s == null || s.length() == 0) return -1;
int ln = s.length();
int[] dp = new int[ln+1];
dp[ln] = 1; // dp[n]=1,处理最后一位是0的情况
dp[ln-1] = s.charAt(ln-1) == '0' ? 0 : 1;
for (int i = ln-2; i >= 0; i--) {
if (s.charAt(i) == '0') dp[i] = 0;
else {
if (Integer.parseInt(s.substring(i, i+2)) <= 26)
dp[i] = dp[i+1] + dp[i+2];
else
dp[i] = dp[i+1];
}
}
return dp[0];
}
最长递增子序列
300,Longest Increasing Subsequence
最长递增子序列
dp [ i ] 表示 arr [ 0 ~ i ] 的最长递增子序列,dp [ i ] = max { 1 , dp [ j ] + 1 | arr[ i ] > arr[ j ] && j < i }
public int lengthOfLIS(int[] nums) {
if (nums.length == 0) return 0;
int[] dp = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
}
int max = dp[0];
for (int i = 1; i < nums.length; i++) {
if (dp[i] > max) max = dp[i];
}
return max;
上面的解法时间复杂度为O(N^2),下面来介绍种O(NlogN)的解法
定义一个数组 ends,ends[ i ] 表示长度为 i + 1 的递增子序列的最小值,这个最小值指的是同样长度的序列组合中,最后一个元素值最小的那个。由此可知 ends 数组还是递增的,那么在查找时就可使用二分法,从而将时间复杂度降低。
我们会遍历 nums 数组,将当前元素与 ends 中元素进行比较,当 ends[ i ] < num <= ends[ i+1 ] 时,ends[ i + 1 ] = num。
public static int lengthOfLIS(int[] nums) {
if (nums.length == 0) return 0;
int[] ends = new int[nums.length];
ends[0] = nums[0];
int right = 0; // 代表此时ends数组最后一个有效位置
int l, m, r; // 用于二分查找
for (int num : nums) {
l = 0;
r = right;
while (l <= r) {
m = l + (r - l) / 2;
if (num > ends[m]) {
l = m + 1;
} else {
r = m - 1;
}
}
// 更新 right 值
right = Math.max(l, right);
// l 位置即是我们要插入的位置
ends[l] = num;
}
return right+1;
}
376, 摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
如:[1,17,5,10,13,15,10,5,16,8] 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
解:将数组 [1,17,5,10,13,15,10,5,16,8] 转换为 [up, down, up, up, up, down, down, up, down];转换依据是 当nums[ i ] - nums[ i - 1 ] > 0, 则记位up,否则为down;则以nums[ i ] 为结尾的摆动序列的最大长度为 前一个down的大小加一。
public int wiggleMaxLength(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int up = 1, down = 1;
for(int i = 1; i < nums.length; i++) {
if (nums[i] > nums[i-1]) up = down + 1;
else if (nums[i] < nums[i-1]) down = up + 1;
}
return Math.max(up, down);
}
最长公共子序列
对于两个子序列 S1 和 S2,找出它们最长的公共子序列。
定义一个二维数组 dp 用来存储最长公共子序列的长度,其中 dp[ i ][ j ] 表示 S1 的前 i 个字符与 S2 的前 j 个字符最长公共子序列的长度。考虑 S1i 与 S2j 值是否相等,分为两种情况:
- 当 S1i == S2j 时,那么就能在 S1 的前 i-1 个字符与 S2 的前 j-1 个字符最长公共子序列的基础上再加上 S1i 这个值,最长公共子序列长度加 1,即 dp[ i ][ j ] = dp[ i-1 ][ j-1 ] + 1。
- 当 S1i != S2j 时,此时最长公共子序列为 S1 的前 i-1 个字符和 S2 的前 j 个字符最长公共子序列,或者 S1 的前 i 个字符和 S2 的前 j-1 个字符最长公共子序列,取它们的最大者,即 dp[ i ][ j ] = max{ dp[ i-1 ][ j ], dp[ i ][ j-1 ] }。
综上,最长公共子序列的状态转移方程为:
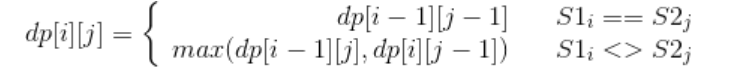
对于长度为 N 的序列 S1 和长度为 M 的序列 S2,dp[N][M] 就是序列 S1 和序列 S2 的最长公共子序列长度。
与最长递增子序列相比,最长公共子序列有以下不同点:
- 针对的是两个序列,求它们的最长公共子序列。
- 在最长递增子序列中,dp[i] 表示以 Si 为结尾的最长递增子序列长度,子序列必须包含 Si ;在最长公共子序列中,dp[i][j] 表示 S1 中前 i 个字符与 S2 中前 j 个字符的最长公共子序列长度,不一定包含 S1i 和 S2j。
- 在求最终解时,最长公共子序列中 dp[N][M] 就是最终解,而最长递增子序列中 dp[N] 不是最终解,因为以 SN 为结尾的最长递增子序列不一定是整个序列最长递增子序列,需要遍历一遍 dp 数组找到最大者。
0-1 背包
有一个容量为 N 的背包,要用这个背包装下物品的价值最大,这些物品有两个属性:体积 w 和价值 v。
定义一个二维数组 dp 存储最大价值,其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。设第 i 件物品体积为 w,价值为 v,根据第 i 件物品是否添加到背包中,可以分两种情况讨论:
- 第 i 件物品没添加到背包,总体积不超过 j 的前 i 件物品的最大价值就是总体积不超过 j 的前 i-1 件物品的最大价值,dp[i][j] = dp[i-1][j]。
- 第 i 件物品添加到背包中,dp[i][j] = dp[i-1][j-w] + v。
第 i 件物品可添加也可以不添加,取决于哪种情况下最大价值更大。因此,0-1 背包的状态转移方程为: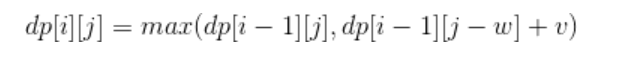
进行空间优化
在程序实现时可以对 0-1 背包做优化。观察状态转移方程可以知道,前 i 件物品的状态仅与前 i-1 件物品的状态有关,因此可以将 dp 定义为一维数组,其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i][j]。此时,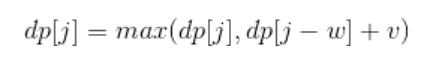
变种:
完全背包:物品数量为无限个。如 322,518
多重背包:物品数量有限制
多维费用背包:物品不仅有重量,还有体积,同时考虑这两种限制。如 474,
来看看相关题目:
416 ,分割等和子集
可以看成一个背包大小为 sum/2 的 0-1 背包问题。
public boolean canPartition(int[] nums) {
if(nums == null) return false;
int sum = 0;
for(int num : nums) sum += num;
if((sum & 1) == 1) return false;
sum /= 2;
boolean[] dp = new boolean[sum+1];
dp[0] = true;
for(int num : nums){
for(int j = sum; j >= num; j--){
dp[j] = dp[j] || dp[j-nums[i-1]];
}
}
return dp[sum];
}
494, 目标和
给定一个非负整数数组,a1, a2, …, an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
该问题可以转换为 Subset Sum 问题,从而使用 0-1 背包的方法来求解
分析后该题转化为:sum( p ) 代表正数的和,sum( n ) 代表负数的和,满足条件:sum( p ) = sum( n ) + S;这就和 416 题 分割等和子集 相同。
public int findTargetSumWays(int[] nums, int S) {
if (nums == null) return 0;
int sum = 0;
for(int num : nums) sum += num;
if (sum < S || ((sum+S) & 1) == 1) return 0;
int target = (sum+S) >> 1;
int[] dp = new int[target+1];
dp[0] = 1;
for(int num : nums) {
for(int i = target; i >= num; i--) {
dp[i] = dp[i] + dp[i-num];
}
}
return dp[target];
}
当然本题还可用 DFS,毕竟动态规划来源于暴力递归,是采用空间换时间的方式来节省提高效率。
public int findTargetSumWays(int[] nums, int S) {
return findTargetSumWays(nums, 0, S);
}
private int findTargetSumWays(int[] nums, int start, int S) {
if (start == nums.length) {
return S == 0 ? 1 : 0;
}
// 每一步无非两种选择,正或负
return findTargetSumWays(nums, start + 1, S + nums[start])
+ findTargetSumWays(nums, start + 1, S - nums[start]);
}
139, 单词拆分
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
- 拆分时可以重复使用字典中的单词。
- 你可以假设字典中没有重复的单词。
单词没有使用次数的限制,因此这是一个完全背包问题。该问题涉及到字典中单词的使用顺序,因此可理解为涉及顺序的完全背包问题。
求解顺序的完全背包问题时,对物品的迭代应该放在最里层。
dp [ i ] 表示字典中是否存在能组成 sArr[ 0~i-1 ] 字符串的组合
public boolean wordBreak(String s, List<String> wordDict){
boolean[] dp = new boolean[s.length()+1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDict.contains(s.substring(j, i))){
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
474, Ones and Zeroes
现在,假设你分别支配着 m 个 0 和 n 个 1。另外,还有一个仅包含 0 和 1 字符串的数组。
你的任务是使用给定的 m 个 0 和 n 个 1 ,找到能拼出存在于数组中的字符串的最大数量。每个 0 和 1 至多被使用一次。
这是一个多维费用的 0-1 背包问题,有两个背包大小,0 的数量和 1 的数量
public int findMaxForm(String[] strs, int m, int n) {
if (strs == null || strs.length == 0) return 0;
// dp[i][j] 代表 i-1个0,j-1个1 数组能够组成的最大个数
int[][] dp = new int[m+1][n+1];
for(String s : strs) {
int zeros = 0, ones = 0;
for(char c : s.toCharArray()) {
if(c == '0') zeros++;
else ones++;
}
for (int i = m; i >= zeros; i--) {
for (int j = n; j >= ones; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i-zeros][j-ones]+1);
}
}
}
return dp[m][n];
}
322.,零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
因为硬币可以重复使用,因此这是一个完全背包问题。完全背包只需要将 0-1 背包中逆序遍历 dp 数组改为正序遍历即可。
public int coinChange(int[] coins, int amount) {
if (coins == null || coins.length == 0 || amount == 0) return 0;
int[] dp = new int[amount+1];
for (int coin : coins) {
for(int j = coin; j <= amount; j++) {
if (j == coin) dp[j] = 1;
else if (dp[j-coin] != 0) {
if(dp[j] == 0) dp[j] = dp[j-coin]+1;
else dp[j] = Math.min(dp[j],dp[j-coin]+1);
}
}
}
return dp[amount] == 0 ? -1 : dp[amount];
}
518, Coin Change 2
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
完全背包问题。
public int change(int amount, int[] coins) {
if (coins == null) return 0;
int[] dp = new int[amount+1];
dp[0] = 1;
for(int coin : coins) {
for(int i = coin; i <= amount; i++) {
dp[i] += dp[i-coin];
}
}
return dp[amount];
}
377, 组合总和 Ⅳ
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
请注意,顺序不同的序列被视作不同的组合。
顺序的完全背包
public int combinationSum4(int[] nums, int target) {
if(nums == null) return 0;
int[] dp = new int[target+1];
dp[0] = 1;
for(int i = 1; i <= target; i++) {
for(int num : nums) {
if (i-num >= 0) dp[i] += dp[i-num];
}
}
return dp[target];
}
来总结下0-1背包及相关变种问题:
对于0-1背包:外层是对数组/字典的遍历,内层是对dp数组的遍历且顺序是从后往前,一位数组/字典中每个元素只能使用一次;可以这样理解:每个数组/字典中的元素都在dp数组中占有一个等于其本值大小的位置,各个元素之间相互叠加直到顶,这样顶部即是答案,保证了非重复性。
对于多重背包:外层是对数组/字典的遍历,内层是对dp数组的遍历且顺序是从前往后。可以这样理解:每个数组/字典中的元素都在dp数组中占有等于其本值大小倍数的位置(倍数从1开始直到越过顶),各个元素叠加,这样就实现了数组/字典元素使用个数不受限制的条件。
对于顺序多重背包:外层是对dp数组的遍历从前到后,内层是数组/字典的遍历。求的是dp数组中每个位置的所有可能。
比较下不同:对于0-1背包,多重背包来说是每个元素所占位置,元素之间相互的叠加;而顺序多重背包,是dp数组种每个位置的所有可能性。