回溯算法采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
找到一个可能存在的正确的答案;
在尝试了所有可能的分布方法后宣告该问题没有答案。
同时回溯算法和深度优先搜索算法关联密切,在某些情况下就是通过深度优先遍历思想实现。
深度优先搜索算法(DFS)是一种用于遍历或搜索树或图的算法。这个算法会尽可能深 的搜索树的分支。当结点 v 的所在边都己被探寻过,搜索将回溯 到发现结点 v 的那条边的起始结点。这一过程一直进行到已发现从源结点可达的所有结点为止。如果还存在未被发现的结点,则选择其中一个作为源结点并重复以上过程,整个进程反复进行直到所有结点都被访问为止。
回溯算法强调了深度优先搜索算法的用途,用一个不断变化的变量在尝试各种可能的过程中,搜索需要的结果。强调了 回退 操作对于搜索的合理性。
搜索问题的解,可以通过 遍历 实现。所以很多教程把「回溯算法」称为暴力解法。因此回溯算法用于 搜索一个问题的所有的解 ,通过深度优先遍历的思想实现。
可以通过具体的例子进行理解:比如:从全排列问题理解回溯算法
给定一个 没有重复 数字的序列(例如[1,2,3]),返回其所有可能的全排列。
总结搜索的方法:按顺序枚举每一位可能出现的情况,已经选择的数字在当前要选择的数字中不能出现。按照这种策略搜索就能够做到不重不漏。这样的思路,可以用一个树形结构表示。
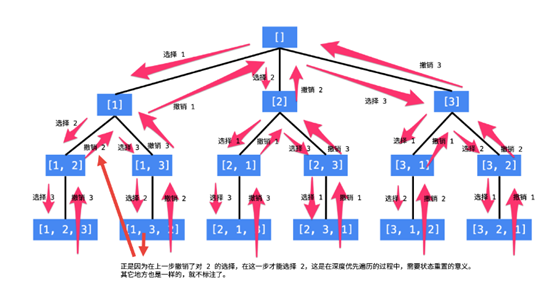
说明:
每一个结点表示了求解全排列问题的不同的阶段,这些阶段通过变量的「不同的值」体现,这些变量的不同的值,称之为「状态」;
使用深度优先遍历有「回头」的过程,在「回头」以后,状态变量需要设置成为和先前一样 ,因此在回到上一层结点的过程中,需要撤销上一次的选择,这个操作称之为「状态重置」;
深度优先遍历,借助系统栈空间,保存所需要的状态变量,在编码中只需要注意遍历到相应的结点的时候,状态变量的值是正确的,具体的做法是:往下走一层的时候,path 变量在尾部追加,而往回走的时候,需要撤销上一次的选择,也是在尾部操作,因此 path 变量是一个栈;
深度优先遍历通过「回溯」操作,实现了全局使用一份状态变量的效果。
使用编程的方法得到全排列,就是在这样的一个树形结构中完成遍历,从树的根结点到叶子结点形成的路径就是其中一个全排列。
设计状态变量(自认为是关键)
首先这棵树除了根结点和叶子结点以外,每一个结点做的事情其实是一样的,即:在已经选择了一些数的前提下,在剩下的还没有选择的数中,依次选择一个数,这显然是一个递归结构;
递归的终止条件是:一个排列中的数字已经选够了 ,因此我们需要一个变量来表示当前程序递归到第几层,我们把这个变量叫做 depth,或者命名为 index ,表示当前要确定的是某个全排列中下标为 index 的那个数是多少;
布尔数组 used,初始化的时候都为 false 表示这些数还没有被选择,当我们选定一个数的时候,就将这个数组的相应位置设置为 true ,这样在考虑下一个位置的时候,就能够以 O(1)O(1) 的时间复杂度判断这个数是否被选择过,这是一种「以空间换时间」的思想。
这些变量称为「状态变量」,它们表示了在求解一个问题的时候所处的阶段。需要根据问题的场景设计合适的状态变量。
代码实现
1. 回溯算法
importjava.util.ArrayDeque;
importjava.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List>permute(int[] nums) {
int len = nums.length;
//使用一个动态数组保存所有可能的全排列
List> res =new ArrayList<>();
if (len == 0) {
return res;
}
boolean[] used = new boolean[len];
Deque path = newArrayDeque<>(len);
dfs(nums, len, 0, path, used, res);
return res;
}
private void dfs(int[] nums, int len, intdepth,
Deque path,boolean[] used,
List> res) {
if (depth == len) {
//必须使用newArrayList<>(path)而不是直接path,直接path会使结果为空
res.add(newArrayList<>(path));
return;
}
for (int i = 0; i < len; i++) {
//如果为used[i]为true表示已选,进行下一次for,i++
if (!used[i]) {
path.addLast(nums[i]);
used[i] = true;
System.out.println(" 递归之前 => " +path);
dfs(nums, len, depth + 1, path,used, res);
used[i] = false;
path.removeLast();
System.out.println("递归之后 => " + path);
}
}
}
public static void main(String[] args) {
int[] nums = {1, 2, 3};
Solution solution = new Solution();
List> lists =solution.permute(nums);
System.out.println(lists);
}
}
2. 非回溯算法(直接复制):
importjava.util.ArrayList;
importjava.util.List;
publicclass Solution {
public List>permute(int[] nums) {
//首先是特判
int len = nums.length;
//使用一个动态数组保存所有可能的全排列
List> res =new ArrayList<>();
if (len == 0) {
return res;
}
boolean[] used = new boolean[len];
List path = newArrayList<>();
dfs(nums, len, 0, path, used, res);
return res;
}
private void dfs(int[] nums, int len, intdepth,
List path,boolean[] used,
List> res) {
if (depth == len) {
// 3、不用拷贝,因为每一层传递下来的 path变量都是新建的
res.add(path);
return;
}
for (int i = 0; i < len; i++) {
if (!used[i]) {
// 1、每一次尝试都创建新的变量表示当前的"状态"
List newPath =new ArrayList<>(path);
newPath.add(nums[i]);
boolean[] newUsed = newboolean[len];
System.arraycopy(used, 0,newUsed, 0, len);
newUsed[i] = true;
dfs(nums, len, depth + 1, newPath,newUsed, res);
// 2、无需回溯
}
}
}
}
参考资料及总结:
参考资料:liweiwei1419 链接:https://leetcodecn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/
可以在链接查看更多相关题型和详细解答。