很多同学可能都还没用过快慢指针，这次就带你们见识一下。这篇文章是由leetcode第141题和第142题引出的。先来容易的，判断链表中是否存在环结构：

141.给定一个链表，判断链表中是否有环

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
如果链表中存在环，则返回 true 。 否则，返回 false 。
进阶：
你能用 O(1)（即，常量）内存解决此问题吗？
示例 1：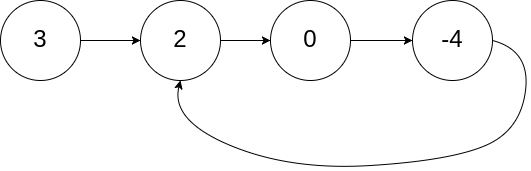

输入：head = [3,2,0,-4], pos = 1
输出：true

解释：链表中有一个环，其尾部连接到第二个节点。

提示：
链表中节点的数目范围是 [0, 104]-105 <= Node.val <= 105，pos 为 -1 或者链表中的一个 有效索引 。

解法一：使用List

解题思路
定义一个List,然后while遍历链表中的节点，对于每次遍历，若List中不存在该节点，则执行add操作，若List中已存在，则返回true，若遍历到null节点则返回false。
代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    List<ListNode>nodes=new ArrayList<>();
    public boolean hasCycle(ListNode head) {
        while(head!=null){
            if(nodes.contains(head)){
                return true;
            }else{
                nodes.add(head);
                head=head.next;
            } 
        }
        return false;        
    }
}

这种解法当然可以实现判断是否有环的目的，但是执行时间为三百多毫秒，再看看题目的进阶要求——使用O(1)的空间，这种解法就有心无力了，因此我们提出第二种解法，也就是今天的主角，快慢指针。

解法二：快慢指针

解题思路
定义快指针fast和慢指针slow，fast每次走两步，slow每次走一步，若链表中存在环结构，则fast与slow一定会在环中相遇，只不过是时间问题而已，这里又涉及到了为什么设置fast每次走两步，走三、四、五步行不行？当然也行，如果面试的时候考官问到了，你可以说根据大量研究实验表明，使用两步所用的相遇时间最短。
代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        if(head==null||head.next==null)return false;
        ListNode fast=head.next;
        ListNode slow=head;
        while(fast!=slow){
            if(fast.next==null||fast.next.next==null)return false;
            slow=slow.next;
            fast=fast.next.next;
        }
        return true;
    }
}

找出环结构后，就上点有难度的，如何找出入环的第一个节点，用额外的list同样可以完成解答，但无法满足题目要求，因此我们讲讲如何用快慢指针来实现。

142. 环形链表 II

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。
进阶：
你是否可以使用 O(1) 空间解决此题？
示例 1：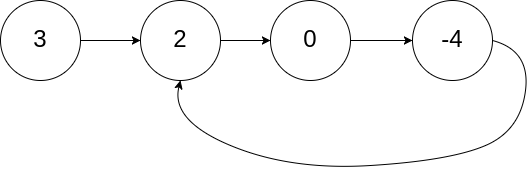

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点

解释：链表中有一个环，其尾部连接到第二个节点。

解题思路
这道题是在141基础上的进阶，同样的，我们使用快慢指针解法，但最难的就是找出进入循环的节点了。借助官方题解的一个图：

图中，头节点到进入循环的节点长度为a，进入循环的节点到相遇节点的长度为b，从相遇节点再到进入循环的节点长度为c，假设相遇时，快指针在环中走了n圈，慢指针在环中走了m圈，则由图可知，快指针走过的路程为：

S1=a+n(b+c);

慢指针走过的路程为：

S2=a+m(b+c);

由于他们到相遇点所用的时间相同且速度已知，则可以推出：

S1/2=S2/1；
即
a+n(b+c)=2(a+m(b+c));

合并同类项得：

a=c+(n-2m-1)(b+c);

也就是：

头节点到进入循环的节点长度=相遇节点到进入循环的节点长度+(n-2m-1)*环的长度；

然后我们转换一下思路，这里是最难理解的，就是将距离与路程的概念区分开来，假想一下，你在一个环中跑步，跑完一圈后与开始的位置相比，你走的路程是一圈，但是你移动的距离其实是0。那么上述公式我们就可以这样说：
头节点到进入循环的节点的距离=相遇节点到进入循环的节点的距离，也就是a=c。后面不管n和m取值为多少，距离都是0。
那么，当快慢指针相遇后，我们只需将快指针重置为头节点的位置，然后让两者每次移动一步，那么它们第二次相遇时即为进入循环的节点所在。
说起来有点绕，但代码很简单：

代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head==null||head.next==null)return null;
        ListNode fast=head.next; //快指针
        ListNode slow=head;//慢指针
        //快慢指针异步前进，直到第一次相遇
        while(fast!=slow){
            if(fast.next==null||fast.next.next==null)return null;
            slow=slow.next; //slow走一步
            fast=fast.next.next;//fast走两步
        }
        //将fast置于头指针位置
        fast=head;
        slow=slow.next;
        //fast与slow同步前进，直到再次相遇
        while(fast!=slow){
            fast=fast.next;
            slow=slow.next;
        }
        return fast;
    }
}

学到的话，不妨点赞加关注吧