用户续费率预测--R语言逻辑回归实例--附带代码和数据集

数据集链接：https://download.csdn.net/download/weixin_41744624/13696323
已经过处理清洗，可直接用于本文模型
………………………………………………………………

a.目的

为了研究用户行为和 用户的特征： 是否续费 存在的关系
本文主要关注预测 是否续费 是否续费 是否续费

b.载入数据集

library(adabag)
library(ROSE)
library(readxl)
library(xlsx)
library(caret)
library(fmsb)
library(tidyverse)
library(rpart)
library(rpart.plot)
library(randomForest)
library(gbm)
library(ggplot2)
library(ggthemes)
#提供describe函数
library(Hmisc)
#提供grid.arrange()函数，用于排列图片
library(gridExtra)
#提供roc函数
library(pROC)
raw_data <- read_excel("Desktop/测试数据集a")

特征概览

View(raw_data)                                                                    

性别、是否到过恋爱阶段、是否续费、购买红娘商品次数、配对数、收到喜欢、被右滑率、拨打次数、接通数、接通5分钟以上次数、红娘曝光次数、红娘消息推荐卡片数、红娘消息页面、推荐卡片喜欢数、精选页推荐卡片数、精选页面点击牵线、推荐页面点击牵线视频约会数、交换微信数、线下见面数

c.训练测试集划分

set.seed(110)
train <- createDataPartition(y=raw_data$是否续费,p=0.8,list=FALSE)
d_train <- raw_data[train,]
d_test <- raw_data[-train,]
str(d_train)

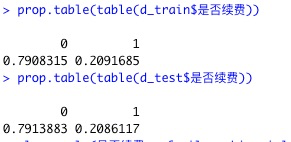
查看目标特征的占比：

prop.table(table(d_train$是否续费))  
prop.table(table(d_test$是否续费)) 

d.逐步回归

目的是为了找到相关性最强的特征指标：

赤池信息准则（Akaike Information Criterion，AIC）：
AIC是衡量统计模型拟合优良性的一种标准，由日本统计学家赤池弘次在1974年提出，它建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。

通常情况下，AIC定义为：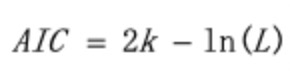

其中k是模型参数个数，L是似然函数。从一组可供选择的模型中选择最佳模型时，通常选择AIC最小的模型。
当两个模型之间存在较大差异时，差异主要体现在似然函数项，当似然函数差异不显著时，上式第一项，即模型复杂度则起作用，从而参数个数少的模型是较好的选择。
一般而言，当模型复杂度提高（k增大）时，似然函数L也会增大，从而使AIC变小，但是k过大时，似然函数增速减缓，导致AIC增大，模型过于复杂容易造成过拟合现象。目标是选取AIC最小的模型，AIC不仅要提高模型拟合度（极大似然），而且引入了惩罚项，使模型参数尽可能少，有助于降低过拟合的可能性。

glm <- glm(是否续费~.,family = binomial(link ='logit'),data = d_train,control = list(maxit = 100))
summary(glm)

logit.step <- step(glm, direction = "both")
summary(logit.step)

drop1(logit.step)

e.逻辑回归模型

选取逐步回归后的特征，构建逻辑回归模型，初步预测

glm <- glm(是否续费 ~ 性别 + 是否到过恋爱阶段  + 购买红娘商品次数 + 红娘曝光次数 +
+                    红娘消息推荐卡片数 +红娘消息页面推荐卡片喜欢数+ 精选页推荐卡片数 +精选页面点击牵线 + 视频约会数 ,
			family = binomial(link ='logit'),data = d_train,control = list(maxit = 100))
pre_test=predict(glm,newdata=d_test,type="response")
summary(pre_test)

f.模型准确性

pre_test=predict(glm,newdata=d_test,type="response")
summary(pre_test)

propability <- 1/(1+exp(-1*pre_test))
summary(propability)

rocCurve=roc(d_test$是否续费,pre_test)
rocCurve$auc

plot(rocCurve, print.auc=TRUE, auc.polygon=TRUE, grid=c(0.1, 0.2),
      grid.col=c("green", "red"), max.auc.polygon=TRUE,
      auc.polygon.col="skyblue", print.thres=TRUE)