B. Minimal Cost
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
There is a graph of n rows and 106+2 columns, where rows are numbered from 1 to n and columns from 0 to 106+1:
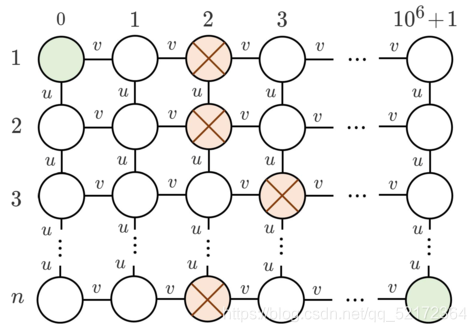
Let’s denote the node in the row i and column j by (i,j).
Initially for each i the i-th row has exactly one obstacle — at node (i,ai). You want to move some obstacles so that you can reach node (n,106+1) from node (1,0) by moving through edges of this graph (you can’t pass through obstacles). Moving one obstacle to an adjacent by edge free node costs u or v coins, as below:
If there is an obstacle in the node (i,j), you can use u coins to move it to (i−1,j) or (i+1,j), if such node exists and if there is no obstacle in that node currently.
If there is an obstacle in the node (i,j), you can use v coins to move it to (i,j−1) or (i,j+1), if such node exists and if there is no obstacle in that node currently.
Note that you can’t move obstacles outside the grid. For example, you can’t move an obstacle from (1,1) to (0,1).
Refer to the picture above for a better understanding.
Now you need to calculate the minimal number of coins you need to spend to be able to reach node (n,106+1) from node (1,0) by moving through edges of this graph without passing through obstacles.
Input
The first line contains a single integer t (1≤t≤104) — the number of test cases.
The first line of each test case contains three integers n, u and v (2≤n≤100, 1≤u,v≤109) — the number of rows in the graph and the numbers of coins needed to move vertically and horizontally respectively.
The second line of each test case contains n integers a1,a2,…,an (1≤ai≤106) — where ai represents that the obstacle in the i-th row is in node (i,ai).
It’s guaranteed that the sum of n over all test cases doesn’t exceed 2⋅104.
Output
For each test case, output a single integer — the minimal number of coins you need to spend to be able to reach node (n,106+1) from node (1,0) by moving through edges of this graph without passing through obstacles.
It can be shown that under the constraints of the problem there is always a way to make such a trip possible.
Example
inputCopy
3
2 3 4
2 2
2 3 4
3 2
2 4 3
3 2
outputCopy
7
3
3
Note
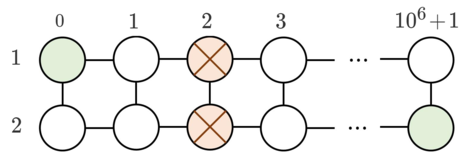
In the first sample, two obstacles are at (1,2) and (2,2). You can move the obstacle on (2,2) to (2,3), then to (1,3). The total cost is u+v=7 coins.
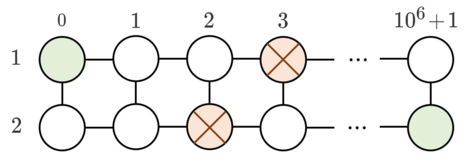
In the second sample, two obstacles are at (1,3) and (2,2). You can move the obstacle on (1,3) to (2,3). The cost is u=3 coins.
对于这个题 水了
水了
刚开始我还以为每一列有多个阻碍物 还是题目看不清楚
既然我们知道每一列就只有一个阻碍物 那么 如果上下阻碍物错位超过1 就说明有空隙 就不用移动障碍物了 如果错位是一 那么就把这个障碍物向上或者向下 或者左右 都可以 取min
C. Pekora and Trampoline
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
There is a trampoline park with n trampolines in a line. The i-th of which has strength Si.
Pekora can jump on trampolines in multiple passes. She starts the pass by jumping on any trampoline of her choice.
If at the moment Pekora jumps on trampoline i, the trampoline will launch her to position i+Si, and Si will become equal to max(Si−1,1). In other words, Si will decrease by 1, except of the case Si=1, when Si will remain equal to 1.
If there is no trampoline in position i+Si, then this pass is over. Otherwise, Pekora will continue the pass by jumping from the trampoline at position i+Si by the same rule as above.
Pekora can’t stop jumping during the pass until she lands at the position larger than n (in which there is no trampoline). Poor Pekora!
Pekora is a naughty rabbit and wants to ruin the trampoline park by reducing all Si to 1. What is the minimum number of passes she needs to reduce all Si to 1?
Input
The first line contains a single integer t (1≤t≤500) — the number of test cases.
The first line of each test case contains a single integer n (1≤n≤5000) — the number of trampolines.
The second line of each test case contains n integers S1,S2,…,Sn (1≤Si≤109), where Si is the strength of the i-th trampoline.
It’s guaranteed that the sum of n over all test cases doesn’t exceed 5000.
Output
For each test case, output a single integer — the minimum number of passes Pekora needs to do to reduce all Si to 1.
Example
inputCopy
3
7
1 4 2 2 2 2 2
2
2 3
5
1 1 1 1 1
outputCopy
4
3
0
Note
For the first test case, here is an optimal series of passes Pekora can take. (The bolded numbers are the positions that Pekora jumps into during these passes.)
[1,4,2,2,2,2,2]
[1,4,1,2,1,2,1]
[1,3,1,2,1,1,1]
[1,2,1,2,1,1,1]
For the second test case, the optimal series of passes is show below.
[2,3]
[1,3]
[1,2]
For the third test case, all Si are already equal to 1.
题目大意: n个蹦床 跟超级玛丽一样 当他跳到这个蹦床的时候
然后跳到 i+a[i]的蹦床 (i+a[i])<=n 然后这个蹦床强度减一
问什么时候啊所有蹦床 强度都为一
思路
对于某一个强度不为一的蹦床 他肯定需要兔子经过a[i]-1次
我们需要算出目前这个不为一的蹦床对后面的贡献是多少就可以
那么贡献是多少呢 对于目前这个蹦床 刚开始 跳到i+a[i] 这时候b[i+a[i]]++; 说明这个位置是从前面跳过来的次数。 然后对于每一个不为一的蹦床 他可以跳[i+2,i+a[i]]的位置 所以对于这个范围的b[]数组 进行++; 如果b[i]>a[i] 说明从前面跳过来的次数 已经把这个位置的蹦床给削掉了 那么 剩余的次数就会贡献给下一个蹦床b[i+1]+=b[i]-a[i]; 最后对b数组清零时注意边界问题
#include<bits/stdc++.h>
#include<stdio.h>
#include<string.h>
using namespace std;
#define PI 3.1415926535897932384626433832795028841971693993751058209749445923078164062
typedef long long ll;
typedef pair<int,int> PII;
int qow_m(int n,int w){int k=1;while(w){if(w&1)k=k*n%1000; n=n*n%1000; w>>=1;}return k%1000;}
ll read(){ll res = 0, ch, flag = 0;if((ch = getchar()) == '-')flag = 1;else if(ch >= '0' && ch <= '9')res = ch - '0';while((ch = getchar()) >= '0' && ch <= '9' )res = res * 10 + ch - '0';return flag ? -res : res;}
const int maxn =1e6+7 ;
//ll sum=0;
ll n,m,k,wz,cnt=0,h,ans=0;
ll mod;
ll x,y=0;
ll a[maxn];
ll b[maxn];
//int sum[maxn];
int main()
{
int T;
cin>>T;
while(T--)
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
ans=0;
for(int i=1;i<=n;i++)
{
if(a[i]!=1)
{
ans+=max(0ll,a[i]-b[i]-1);
}
for(int j=n;j>i+1;j--)
{
if(j-i<=a[i])
b[j]++;
}
ll z = b[i] - a[i] + 1;
b[i+1] += max(z,(ll)0);
}
for(int i=1;i<=n+5;i++) b[i]=0;
cout<<ans<<endl;
}
return 0;
}