题目信息

In how many ways can you tile a 3xn rectangle with 2x1 dominoes?
Here is a sample tiling of a 3x12 rectangle.
有多少种方法可以用2x1多米诺骨牌平铺3xn矩形？
下面是3x12矩形的平铺示例。

输入

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.
输入由几个测试用例组成，最后一行是一个-1。每个测试用例都是一行，包含一个整数’0<=n<=30’。

输出

For each test case, output one integer number giving the number of possible tilings.
对于每个测试用例，输出一个整数，给出可能的平铺数。

测试样例

2
8
12
-1

3
153
2131

来源

Waterloo local 2005.09.24

解答

#include<iostream>

#define ll long long
using namespace std;

ll num[40];

int main()
{
    //freopen("E://test.txt", "r", stdin);
    ios::sync_with_stdio(false);
    int n;
    num[0] = 1;
    num[1] = 0;
    num[2] = 3;
    for (int i = 3; i <= 35; i++)
    {
        if (i % 2 != 0)
        {
            num[i] = 0;
        }
        else
        {
            num[i] = num[i - 2] * 4 - num[i - 4];
        }
    }
    while (cin >> n)
    {
        if (n == -1)
        {
            break;
        }

        cout << num[n] << endl;
    }
    return 0;
}

想法

首先能确定的是奇数个一定不能凑齐
那么来考虑偶数个的情况，两个的时候会有三种情况：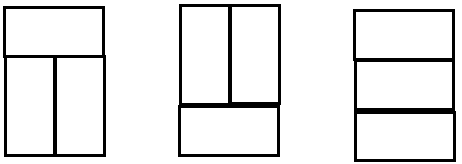

若干个（偶数 i - 2）填满的情况下，在填上两个总数变成（ i 个）为三种情况，即f[i] += f[i-2]*3
下面来考虑把i切割为i - 4和4的情况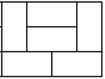

便会多出来这种情况，一正一反两种情况，即f[i] += f[i-4] * 2

最终：f[n] = 3 * f[n-2] + 2 * f[n-4] + 2 * f[n-6] + … + 2 * f [0]
将n - 2代换n得f[n-2] = 3 * f[n-4] + 2 * f[n-6] + 2 * f[n-8]+ … + 2 * f[0]

两式计算化简得f[n] = 4*f[n-2] - f[n-4]