汉诺塔问题简述：

首先声明，本文主要从数学角度分析汉诺塔问题，得到通项公式后再利用递归求解。

汉诺塔问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

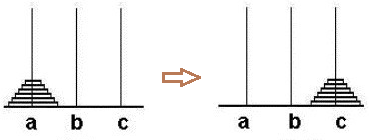
规则总结：1. 一次只允许移动一个轮盘。 2. 小轮盘上方不可放置大轮盘。3. 最后将所有轮盘移动至右方空着的柱子。

问题分析：

我们先来观察一下，在移动轮盘的过程中，有没有出现相似的“模式”。

上图便是这个问题中，一定会出现的一个模式，其他模式和此类似，见后图。

设原来有 $n$ 个轮盘，并且设将$n$个轮盘移动至另一个柱子至少需要耗费$H(n)$步，则上图所需步骤至少耗费$H(n-1)$步。

随后要做的就是将a柱上的大轮盘移动至c柱。

此刻得到的模式是不是有些眼熟？因为c上放的是最大的轮盘，所以任何轮盘都可以放在c上，换句话来讲，现在的状态，和下图没有区别。

没错，我们经历了一次“轮回”，又回到了熟悉的开始，现在我们的任务仍然是将a柱上的所有轮盘，移动至c上，而和刚开始唯一不同的是，我们在a柱上的轮盘从$n$个变为了$n-1$个。我们发现了以下的规律：

$$H(n)=H(n-1)+1+其他移动$$

那么其他移动又是什么东西呢？其实如果聪明的朋友已经发现规律了，就是不断循环上述模式，如下图所示：

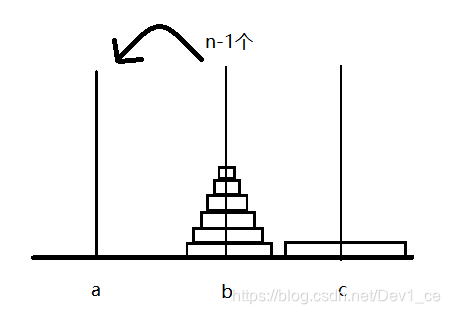
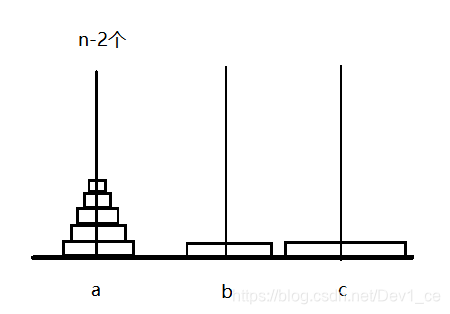
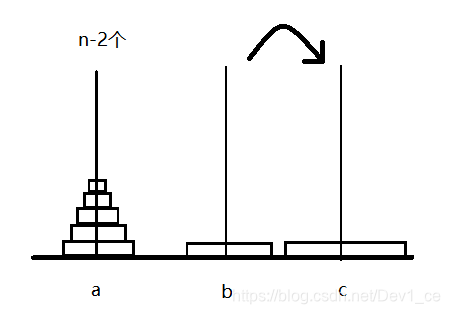
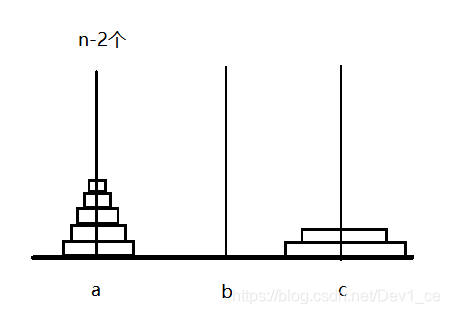
各位，是不是又有一种似曾相识的感觉？如果将c上的两个轮盘遮盖住，我们就又回到了起点，而且a上的轮盘还减少了，变为了$n-2$。事实上，我们确实可以将c柱上的轮盘遮盖起来不看，原因就是因为，此刻c柱上的轮盘为第一大和第二大，换句话来讲，所有在a上的轮盘都可以自由的放在c柱上，此刻的c柱，也就等价于一个空柱子，对放入轮盘没有任何限制。

综上，我们便能得到以下最原始的递推公式

$$H(n)=H(n-1)+1+H(n-2)+1+...+H(2)+1+H(1)+1,H(1)=1$$化简即为
$$H(n)=H(n-1)+H(n-2)+...+H(2)+H(1)+n-1$$随后利用相邻两项做差：
$$H(n+1)=H(n)+H(n-1)+...+H(2)+n$$最后得到：
$$H(n)=2H(n-1)+1$$

编程环节：

有了公式，那么代码也就简单很多了，利用Python的递归，即1. 函数调用自身。2. 设置正确返回与中止条件。

def H(n):
    if n == 1:
        return 1
    else:
        return 2 * H(n-1) + 1

以上为全部代码，当$n=1$时，只需要移动一次就能完成任务，所以$H(1)=1$。这个函数会不断地调用自己，一直到$n=1$，从而实现递归。

不妨来看看$n=4$时的情况：

$$H(4)=2H(3)+1$$

$$H(3)=2H(2)+1$$

$$H(2)=2H(1)+1$$

$$H(1)=1$$

总结：其实如果能得到递推公式，编程实现是非常简单的事情，难处就是如何从一个游戏中，发现其本质、内在的规律，并且用数学的语言加以概括，所以编程最核心的，还是对事物运行的逻辑总结。