《算法导论》第四章-第4节_练习（参考答案）

算法导论（第三版）参考答案：练习4.4-1，练习4.4-2，练习4.4-3，练习4.4-4，练习4.4-5，练习4.4-6，练习4.4-7，练习4.4-8，练习4.4-9

Exercise 4.4-1

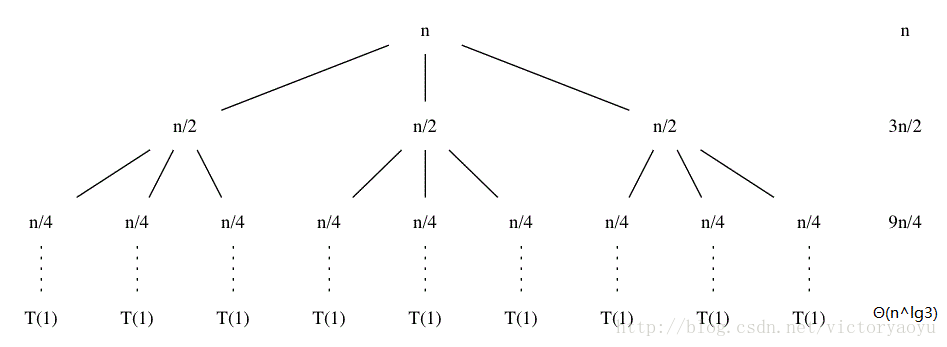
Use a reccursion tree to determine a good asymptotic upper bound on the recurrence $T(n)=3T(⌊n/2⌋)+n$. Use the substitution method to verify your answer.

假设 $n$是2的幂（忍受不精确），则递归树为

注：请看更正版，一个更好的渐进紧确界。

树高 $\lg{n}$，叶节点数量为 $3^{\lg{n}}=n^{\lg{3}}$，整棵树的代价：

$$\begin{align} T(n) &= n+(\frac{3}{2})n+(\frac{3}{2})^2n+ \cdots + (\frac{3}{2})^{\lg{n}-1}n+ \Theta(n^{\lg{3}}) \\ &= \sum_{i=0}^{\lg{n}-1}\Big(\frac{3}{2}\Big)^i n + \Theta(n^{\lg3}) \\ &= n\frac{(3/2)^{\lg{n}} - 1}{(3/2) - 1} + \Theta(n^{\lg3}) \\ &\lt n\frac{(3/2+1/2)^{\lg{n}} - 1}{(3/2) - 1} + \Theta(n^{\lg3}) \\ &\lt n\frac{n - 1}{(3/2) - 1} + \Theta(n^{\lg3}) \\ &= O(n^2) \end{align}$$
代入法证明 $T(n) \le cn^{2}+2n$:
$$\begin{align} T(n) & \le 3c(n/2)^{2} + 2 \cdot n/2 + n \\ &= \frac{3}{4}cn^{2} + 2n \\ &\le cn^2 + 2n \\ \end{align}$$
$O(n^2)$为 $T(n)$的一个渐进上界。

更正：

$$\begin{align} T(n) &= n+(\frac{3}{2})n+(\frac{3}{2})^2n+ \cdots + (\frac{3}{2})^{\lg{n}-1}n+ \Theta(n^{\lg{3}}) \\ &= \sum_{i=0}^{\lg{n}-1}\Big(\frac{3}{2}\Big)^i n + \Theta(n^{\lg3}) \\ &= n\frac{(3/2)^{\lg{n}} - 1}{(3/2) - 1} + \Theta(n^{\lg3}) \\ &= 2n(\frac{3^{\lg{n}}}{n}-1) + \Theta(n^{\lg3}) \\ &= 2 \cdot 3^{\lg{n}}-2n + \Theta(n^{\lg3}) \\ &= O(n^{\lg(3)}) \end{align}$$
代入法证明 $T(n) \le cn^{\lg{3}}+2n$:
$$\begin{align} T(n) & \le 3c(n/2)^{\lg{3}} + 2 \cdot n/2 + n \\ &= cn^{\lg{3}} + 2n \\ &= O(n^{\lg{3}}) \\ \end{align}$$
$O(n^{\lg{3}})$为 $T(n)$的一个渐进上界。

Exercise 4.4-2

Use a reccursion tree to determine a good asymptotic upper bound on the recurrence $T(n)=T(n/2)+n^2$. Use the substitution method to verify your answer.

树高 $\lg{n}$，叶节点数量为 $1$，整棵树的代价：

$$\begin{align} T(n) &= n^2 + \frac{1}{4}n^2 + (\frac{1}{4})^2n^2 + \cdots + (\frac{1}{4})^{\lg{n}-1}n^2 + T(1) \\ &= \sum_{i=0}^{\lg{n}-1}\Big(\frac{1}{4}\Big)^i n^2 + T(1) \\ &< n^2 \sum_{i=0}^{\infty}\Big(\frac{1}{4}\Big)^i + T(1) \\ &= n^2 \frac{1}{1-1/4} + T(1) \\ &= O(n^2) \end{align}$$
证明 $T(n) \le cn^2$
$$\begin{align} T(n) & \le c(n/2)^2 + n^2 \\ & \le cn^2/4 + n^2 \\ & \le (c/4 + 1)n^2 \qquad (c > 4/3) \\ & \le cn^2 \end{align}$$
得证。

Exercise 4.4-3

Use a reccursion tree to determine a good asymptotic upper bound on the recurrence $T(n)=4T(n/2+2)+n$. Use the substitution method to verify your answer.

树高 $\lg{n}$，叶节点数量为 $4^{\lg{n}}=n^{2}$，整棵树的代价：

注：以下递归树求解有误，请略过。看更正版（上图递归树形状不变，其中常数项代价需更改）

$$\begin{align} T(n) &=n + \big((4\cdot \frac{1}{2})n + 4 \cdot 2 \big)+ \big((4^2 \cdot (\frac{1}{2})^2)n + 4^2 \cdot 2 \big) + \cdots + \big((4^{\lg{n-1}} \cdot (\frac{1}{2})^{\lg{n-1}})n + 4^{\lg{n-1}} \cdot 2 \big) + \Theta(n^2) \\ &= \sum_{i=0}^{\lg{n}-1}\Big(2^i n + 2^{2i+1}) + \Theta(n^2) \\ &= \sum_{i=0}^{\lg{n}-1}2^i n + 2\sum_{i=0}^{\lg{n}-1}4^i + \Theta(n^2) \\ &=n\frac{2^{\lg{n}} - 1}{2 - 1} + 2\frac{4^{\lg{n}} - 1}{4 - 1} + \Theta(n^2) \\ &= n^2 - n + 2\frac{n^{2} - 1}{3} + \Theta(n^2) \\ &= \Theta(n^2) \end{align}$$

更正:

$$\begin{align} T(n) &=n + \Big((4\cdot \frac{1}{2})n + 4 \cdot (2) \Big)+ \Big((4^2 \cdot (\frac{1}{2})^2)n + 4^2 \cdot (1+2) \Big) + \Big((4^3 \cdot (\frac{1}{2})^3)n + 4^3 \cdot (\frac{1}{2}+1+2) \Big) + \\ & \quad \cdots + \Big((4^{\lg{n-1}} \cdot (\frac{1}{2})^{\lg{n-1}})n + 4^{\lg{n-1}} \cdot \big(\frac{1}{2}^{\lg{n}-3}+\cdots+2\big) \Big) + \Theta(n^2) \\ &= \sum_{i=0}^{\lg{n}-1}(2^i n) + \sum_{i=1}^{\lg{n}-1}(4^{i+1}-2^{i+2}) + \Theta(n^2) \\ &= \sum_{i=0}^{\lg{n}-1}(2^i n) + \sum_{i=2}^{\lg{n}}4^{i} - 4\sum_{i=1}^{\lg{n}-1}2^{i} + \Theta(n^2) \\ &= n\frac{2^{\lg{n}} - 1}{2 - 1} + \frac{8-4^{\lg{n}+1}}{1-4} + 4\frac{2-2^{\lg{n}}}{1-2} + \Theta(n^2) \\ &= n^2 - n +\frac{1}{3}(4n^2-8) + 4n - 8 + \Theta(n^2)\\ &= \Theta(n^2) \end{align}$$
证明 $T(n) \le cn^2 + 2n$
$$\begin{align} T(n) & \le 4c(n/2)^2 + 2 \cdot n/2 + n \\ & \le cn^2 + 2n \\ \end{align}$$

得证 $T(n)=O(n^2)$。

Exercise 4.4-4

Use a reccursion tree to determine a good asymptotic upper bound on the recurrence $T(n)=2T(n−1)+1$. Use the substitution method to verify your answer.

树高 $n-1$，叶节点数量为 $2^{n-1}$，整棵树的代价：

$$T(n)= 1+2+4+\cdots+2^{n-2}+\Theta(2^{n-1}) = 2^{n-1}-1+\Theta(2^{n-1}) = \Theta(2^n)$$
证明 $T(n) < c2^n + n$
$$\begin{align} T(n) & \le 2c2^{n-1} + (n - 1) + 1 \\ & \le c2^n + n \\ \end{align}$$
得证 $T(n)=O(2^n)$。

Exercise 4.4-5

Use a reccursion tree to determine a good asymptotic upper bound on the recurrence $T(n)=T(n−1)+T(n/2)+n$. Use the substitution method to verify your answer.

画图可知递归树不是完全二叉树，从 $\lg{n}$到 $n-1$层为非完全的。求整棵树代价中，可以推测 $T(n)=O(2^n)$

证明 $T(n) \le c2^n - 4n$

$$\begin{align} T(n) & \le c2^{n-1} - 4(n-1) + c2^{n/2} - 4n/2 + n \\ & \le c(2^{n-1} + 2^{n/2}) - 5n + 1 & (n > 1/4) \\ & \le c(2^{n-1} + 2^{n/2}) - 4n & (n > 2)\\ & \le c(2^{n-1} + 2^{n-1}) - 4n \\ & \le c2^n - 4n \\ \end{align}$$
得证 $T(n)=O(2^n)$

Exercise 4.4-6

Argue that the solution to the recurrence $T(n)=T(n/3)+T(2n/3)+cn$, where c is a constant, is $Ω(n\lg{n})$by appealing to the recurrsion tree.

递归树直到 $\log_{3}{n}$后才开始变得不完全，加上每层代价都为 $cn$，所以 $T(n) \ge Ω(n\log_{3}{n}) = Ω(n\lg{n})$。

Exercise 4.4-7

Draw the recursion tree for $T(n)=4T(⌊n/2⌋)+cn$, where $c$is a constant, and provide a tight asymptotic bound on its solution. Verify your answer with the substitution method.

树高 $\lg{n}$，叶节点数量为 $4^{\lg{n}}=n^{2}$，整棵树的代价：

$$\begin{align} T(n) &= cn + 2cn + 4cn + \cdots + 4^{\lg{n}-1} \frac{cn}{2^{\lg{n}-1}} + \Theta(n^2) \\ &= \sum_{i=0}^{\lg{n}- 1}2^icn + \Theta(n^2) \\ &= cn \frac{2^{\lg{n}} - 1}{2 - 1} + \Theta(n^2) \\ &= \Theta(n^2) \end{align}$$
证明 $T(n) \le cn^2 + 2cn$
$$T(n) \le 4c(n/2)^2 + 2cn/2 + cn = cn^2 + 2cn$$
证明 $T(n) \ge cn^2 + 2cn$
$$T(n) \ge 4c(n/2)^2 + 2cn/2 + cn = cn^2 + 2cn$$
得证 $T(n) = \Theta(n^2)$。

Exercise 4.4-8

Use a recursion tree to give an asymptotically tight solution to the recurrence $T(n)=T(n−a)+T(a)+cn$, where $a≥1$and $c>0$are constants.

树高 $n/a$（假设 $n$能被 $a$整除），叶节点数量为 $2$，整棵树的代价：

$$\begin{align} T(n) &= cn + cn + c(n-a) + c(n-2a) + \cdots + c\Big(n-(\frac{n}{a}-1)a+a\Big) + \Theta(1) \\ &= cn^2/a + c(\frac{n}{a}-1)a - \sum_1^{\frac{n-1}{a}-1} c\cdot i\cdot a + \Theta(1) \\ &= \Theta(n^2) + \Theta(n) - \Theta(n) + \Theta(1) \\ &= \Theta(n^2) \end{align}$$
尝试用代入法，证明 $T(n) \le cn^2$
$$\begin{align} T(n) & \le c(n-a)^2 + ca + cn \\ &= cn^2 - 2acn + ca^2 + ca + cn \\ &= cn^2 - cn(2a - 1) + ca^2 + ca & (a \ge1 > 1/2,\ n > \frac{a^2+a}{2a-1}) \\ & \le cn^2 \\ & = O(n^2) \end{align}$$
证明 $T(n) \ge c(n+1)^2$(这部分有trick)
$$\begin{align} T(n) & \ge c(n-a)^2 + ca + cn \\ &= cn^2 - 2acn + ca^2 + ca + cn \\ & = cn^2 - c(2an - a - n) & (a < 1/2, n > 2a) \\ & \ge cn^2 + cn \\ & \ge cn^2 \\ & = \Theta(n^2) \end{align}$$
决策树给出了精确值，可是代入法证明失败了。

Exercise 4.4-9

Use a recursion tree to give an asymptotically tight solution to the recurrence $T(n)=T(αn)+T((1−α)n)+cn$, where α is a constant in the range $0<α<1$, and $c>0$is also a constant.

类似练习4.4-6。假设 $α$更大，则树高 $\lg_{\frac{1}{α}}{n}$。整棵树在 $\lg_{\frac{1}{1-α}}{n}$以上，每一层次代价都为 $cn$，所以

$$T(N) \le cn \cdot \lg_{\frac{1}{1-α}}{n} \le cn \cdot \lg{n} \qquad \big((1-α)\le \frac{1}{2}\big)$$
即 $T(n)=Ω(n\lg{n})$

代入法证明 $T(n) \le dn\lg{n}$

$$\begin{align} T(n) & \le d \alpha n \lg(\alpha n) + c (1-\alpha) n \lg\big((1-\alpha) n\big) + cn \\ &= d \alpha n \lg{n} + d (1-\alpha) n \lg{n} + d \alpha n \lg\alpha + d (1-\alpha) n \lg(1-\alpha) + cn \\ & \le d n \lg{n} + \big(d (\alpha \lg\alpha + (1-\alpha) \lg(1-\alpha)) + c\big)n\\ & \le d n \lg{n} \end{align}$$
只要 $d \ge \frac{-c}{\alpha\lg\alpha + (1-\alpha)\lg(1-\alpha)}$， $T(n)=O(n\lg{n})$。

所以 $T(n)=\Theta(n\lg{n})$。