目录
前言
前言,由于饱和函数或者连续光滑的双曲函数作为切换函数时对滑模控制输出的消抖有限,所以本文想学习以下滤波器消抖的方法,下面先介绍简单的低通滤波器消抖的滑模控制,并配上实例及程序模型进行仿真分析。
1.低通滤波器原理
其实也有的文献称为线性滤波,具体可以参考以下文献:
Design of Sliding Mode Controller with Low-Pass Filter for Robot Manipulators
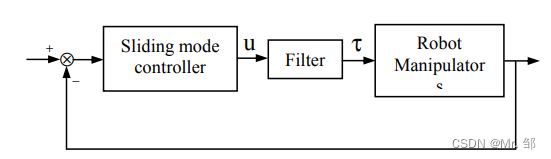
带滤波器的滑膜控制系统结构
一阶低通滤波器:
![]()
其中,λ > 0。
由系统结构图可知:τ = u*Q(s) = u*λ/(s+λ),即τ'+λτ = λu。其中τ为滤波后的控制输入(实际控制输入),u为滤波前的控制输入(虚拟控制输入)。
2.控制器设计
2.1被控对象
Jθ''=u-d(t)
其中,J = 1/10,扰动d(t) = 3*sin(t)。
2.2误差变量
e = θ-θd
其中,θd为指令信号/理想信号。
2.3滑膜函数
s = e''+c1*e'+c2*e
其中,c1和c2的取值需要满足使滑膜函数s多项式为Hurwitz多项式。
将e'''和被控对象u=Jθ''+d(t)代入滑膜函数中,所以有:
s' = λu-d'-λ(Jθ''+d)+J(-θd''+c1*e''+c2e')
还是用等效滑模的思想,先假设扰动d(t) = 0,则s' = λu-λJθ''+J(-θ''d+c1*e''+c2e'),为了方便调参,选取等速趋近律s' = -η*sign(s),联立函数导函数和趋近律,得控制律(虚拟控制输入):
u = -(-λ*J*θ''+J*(-θd''+c1*e''+c2*e')+η*sign(s))
至于使用Lyapunov函数证明闭环系统的稳定性,这里不再累赘,有兴趣读者可以看我之前的文章。
3.MATLAB/Simulink仿真分析
3.1s函数编写被控对象
指定信号/理想信号θd = sin(t),扰动d(t) = 3*sin(t)。
function [sys,x0,str,ts,simStateCompliance] = Plant(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 2;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [0.5;0];
str = [];
ts = [0 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
theta = x(1);
dtheta = x(2);
d = u(1);%扰动d(t)
tau = u(2);%实际控制输入τ
J = 10;
ddtheta = (tau-d)/J;
sys = [dtheta;ddtheta];
function sys=mdlUpdate(t,x,u)
sys = [];
function sys=mdlOutputs(t,x,u)
sys = x;
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];3.2s函数编写控制器
function [sys,x0,str,ts,simStateCompliance] = Controller(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 4;
sizes.NumInputs = 4;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [0 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
sys = [];
function sys=mdlUpdate(t,x,u)
sys = [];
function sys=mdlOutputs(t,x,u)
theta = u(3);
dtheta = u(4);
ddtheta = u(2);
thetad = u(1);%sin(t)
dthetad = cos(t);%不能使用diff求导是因为diff只能用于符号(syms)函数的求导,不能在fcn模块中用diff也同理
ddthetad = -sin(t);
dddthetad = -cos(t);
J = 10;%
lambda = 25;%低通滤波器参数
c1 = 10;c2 = 10;%滑模面系数
eta = 80;%趋近律调节参数
e = theta-thetad;
de = dtheta-dthetad;
dde = ddtheta-ddthetad;
s = dde+c1*de+c2*e;
ut = -(-lambda*J*ddtheta+J*(-dddthetad+c1*dde+c2*de)+eta*sign(s))/lambda;%虚拟控制输入
sys = [ut;dthetad;e;de];
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];3.3Simulink模型
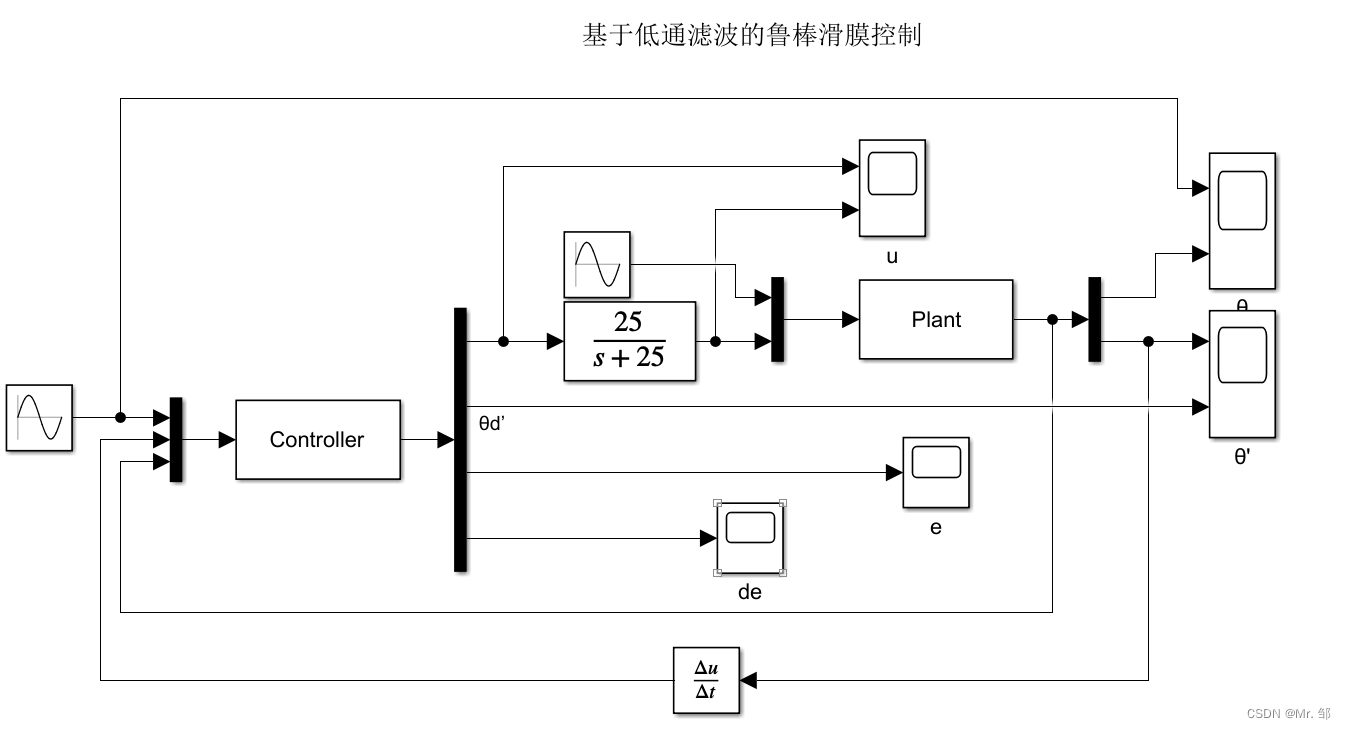
3.4结果分析
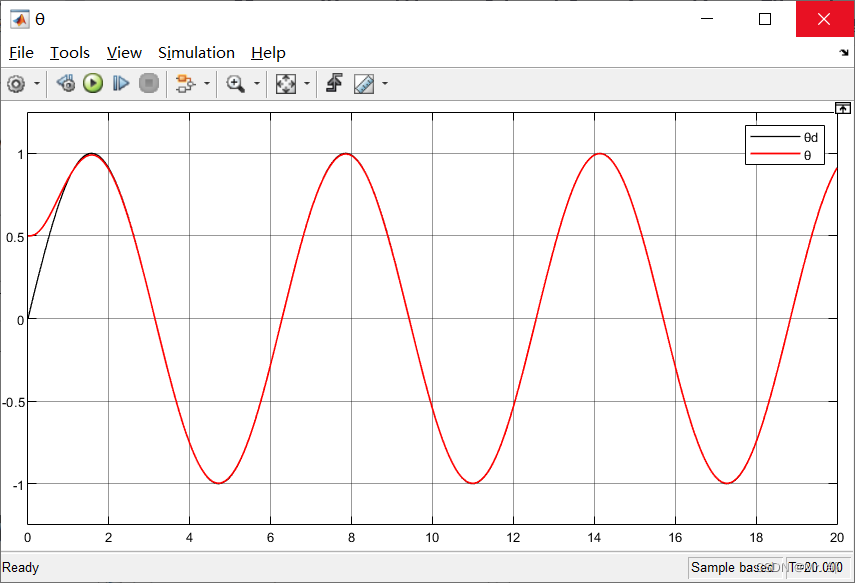
角度θ
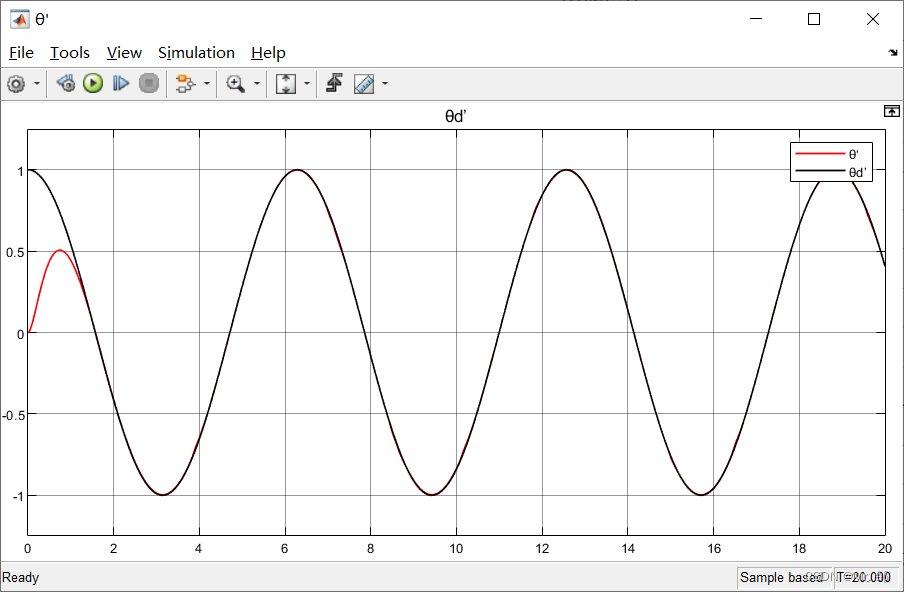
角速度θ'
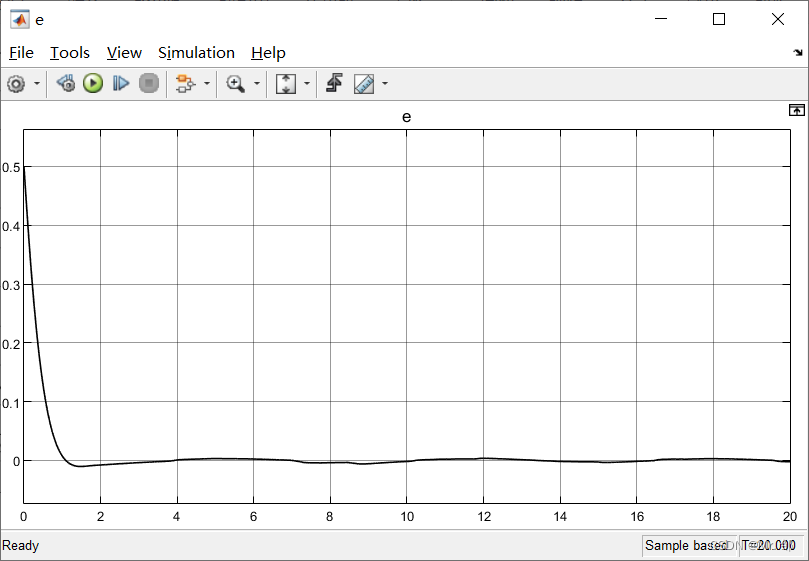
误差e
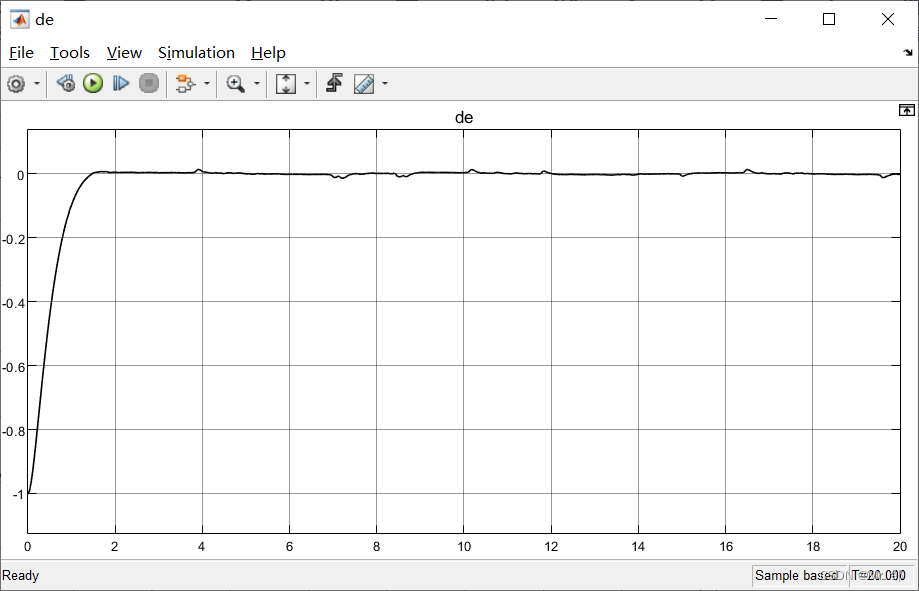
误差变化率de
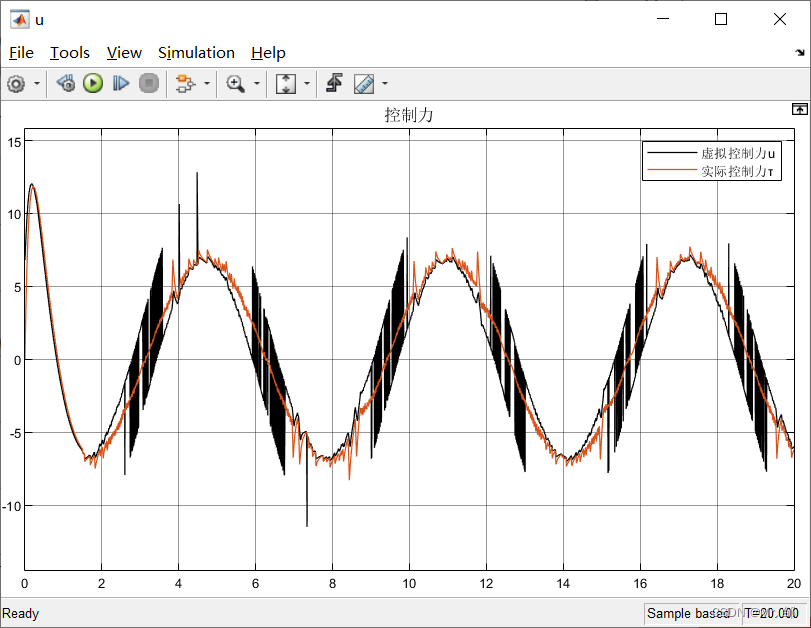
虚拟控制力u与实际控制里τ
结论:经过调参,可以发现系统在2s内实现完美追踪指令信号;另外经过低通滤波器,控制输入的抖阵得到了很大的改善,证明了基于低通滤波器的滑膜控制有效性。
4.注意事项
4.1编写s函数
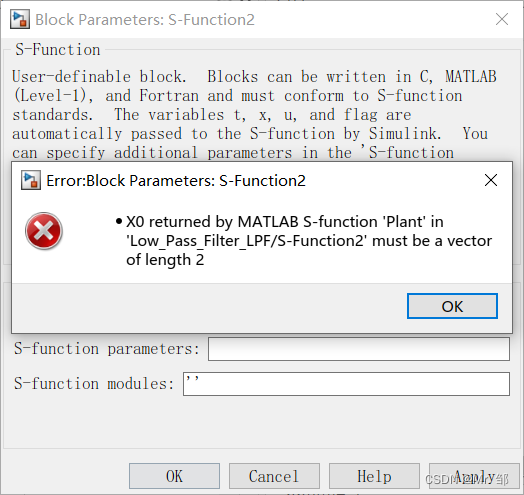
常见的报错原因:s函数编写时状态初值未赋值,即
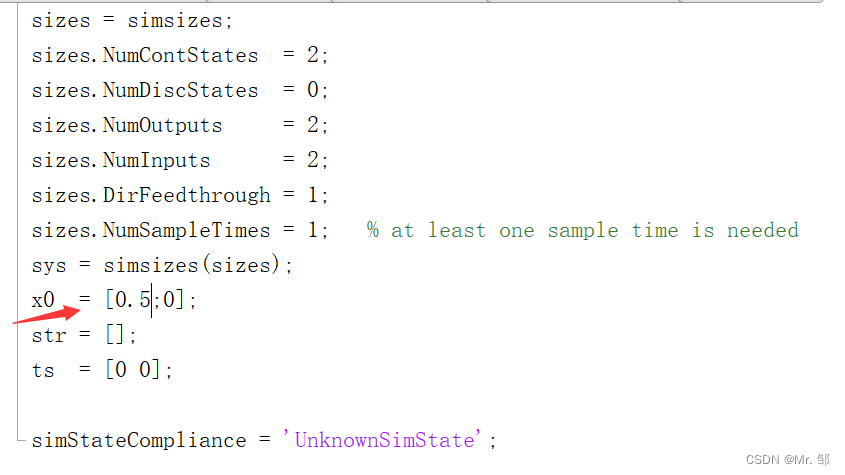
4.2调参
本案例需要调节的参数有:滤波器算子λ、滑模系数c1和c2、趋近律参数η。需要调节的参数较多,读者可以自己将我的程序分析。博主会发现:
滤波器算子λ、滑模系数c1和c2越小效果越好;趋近律参数η需要大一些较好。(如有错误欢迎指正)
学习问题:
1.但是还是没有解决当追踪信号不好求导时,不能用derivative模块进行求导的问题,但是经查阅,是说derivative模块连续用两次结果是不正确的,具体可以见如下以及博客的评论:
Simulink中sine wave的两次微分再两次积分的图像差异问题 - 知乎
所以如果遇到复杂些的、没有函数的追踪指令信号该如何求其导数呢?还是没能解决。
2.滑膜函数的项数取几项,有什么依据吗?(有大佬知道恳请指导,谢谢!)
如果有帮助,麻烦帮忙点个赞是我最大的分享动力,非常感谢!
注:仅为便利自己学习,错误在所难免,如有侵权,请联系删除,有兴趣的学者可以参考学习交流,谢谢!
参考资料:
《滑模变结构控制MATLAB仿真:基本理论与设计方法第四版》---刘金琨