文章目录
1. 卷积拓展至非欧式空间
1.1 卷积的理解
称 ( f ∗ g ) ( n ) (f*g)(n)(f∗g)(n) 为 f , g f,gf,g 的卷积,其连续的定义为:
( f ∗ g ) ( n ) = ∫ − ∞ ∞ f ( τ ) g ( n − τ ) d τ (f * g)(n)=\int_{-\infty}^{\infty} f(\tau) g(n-\tau) d \tau(f∗g)(n)=∫−∞∞f(τ)g(n−τ)dτ
离散定义为
( f ∗ g ) ( n ) = ∑ τ = − ∞ ∞ f ( τ ) g ( n − τ ) (f * g)(n)=\sum_{\tau=-\infty}^{\infty} f(\tau) g(n-\tau)(f∗g)(n)=τ=−∞∑∞f(τ)g(n−τ)
这两个式子有一个共同的特征:
1.2 卷积神经网络拓展至非欧空间
| 欧式空间卷积神经网络 | 非欧式空间结构数据 |
|---|---|
| 处理固定输入维度数据、局部输入数据必须有序 | 局部输入维度可变 |
| 语音、图像、视频(规则结构)满足以上两点要求 | 局部输入排列无序 |
1.2.1 活性卷积
传统的卷积是对每个处在规格 格子空间上的数据进行聚合,并且聚合使用的参数是一样的。而如果数据发生了 偏移,不再是处在规格的格子空间上,那就不能直接使用基本的卷积了,为了更好的拟合这种数据,最好的办法是让 卷积核形状可以自己去学习,于是提出了活性卷积。
活性卷积 (Yunho et al. CVPR 2017) 的特点:
- 双线性插值:离散坐标下,可以通过插值方法计算得到连续位置的像素值;
- 可学习参数 Δ α k Δ β k \Delta \alpha_{k} \Delta \beta_{k}ΔαkΔβk;
- 可变卷积核形状固定。[难点]
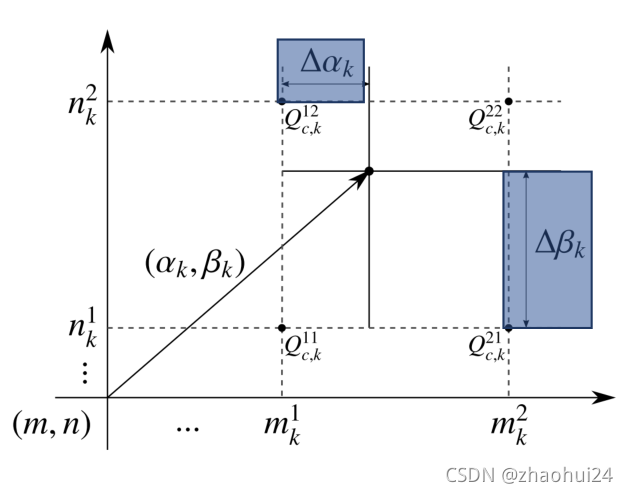
上图中,m k 1 , m k 2 , n k 1 , n k 2 m_{k}^{1}, m_{k}^{2}, n_{k}^{1}, n_{k}^{2}mk1,mk2,nk1,nk2 是离散坐标系中的一个整数坐标,它所对应的四个点是 Q c , k 11 , Q c , k 21 , Q c , k 12 , Q c , k 22 Q_{c, k}^{11}, Q_{c, k}^{21}, Q_{c,k}^{12}, Q_{c, k}^{22}Qc,k11,Qc,k21,Qc,k12,Qc,k22 ,这时候出现了一个有偏移的数据(箭头黑点处),离散坐标不知道,引入两个偏移量 Δ α k , Δ β k \Delta\alpha_{k}, \Delta \beta_{k}Δαk,Δβk,它们是可学习的。
通过双线性插值的方式,得到这个偏移的数据点处的像素值应该由邻近的 Q c , k 11 , Q c , k 21 , Q c , k 12 , Q c , k 22 Q_{c, k}^{11}, Q_{c,k}^{21}, Q_{c, k}^{12}, Q_{c, k}^{22}Qc,k11,Qc,k21,Qc,k12,Qc,k22 这四个点决定的。然后通过梯度反向传播的方式,对 Δ α k , Δ β k \Delta\alpha_{k} ,\Delta \beta_{k}Δαk,Δβk 进行求解。
这种活性卷积可以解决欧式空间中数据排列出现一定偏差的情况,但也存在一些问题,比如 Δ α k , Δ β k \Delta \alpha_{k},\Delta \beta_{k}Δαk,Δβk 学习出来就是固定的,不会随数据而变化,也就是说这种活性卷积在一个数据集上学习完之后 Δ α k , Δ β k \Delta\alpha_{k}, \Delta \beta_{k}Δαk,Δβk 就固定下来了,对所有的数据都是采用相同的 Δ α k , Δ β k \Delta \alpha_{k}, \Delta \beta_{k}Δαk,Δβk,这显然不够理想。参考链接2
1.2.2 可变形卷积
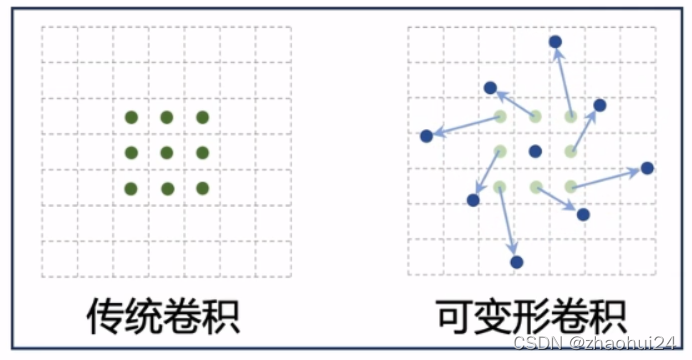
为了使卷积核的形状是数据驱动的,也就是说对不同的数据可以自适应的产生专门的卷积核,去做一个局部的聚合操作,于是就有了可变形卷积。[难点]
传统的卷积是在一个规则的格子上做一个局部的聚合,而可变性卷积相当于在一个不规则的格子上做一个聚合,其中箭头表示格子的一个偏移量,这个偏移量是通过数据驱动学习的。
在此框架下,由于卷积核是通过数据驱动的方式学习的,对于不同的输入数据学习到的卷积核形状是不一样的,所以实现了卷积核位置的参数化;其次,这种数据驱动方式学习出来的卷积核的偏移量是连续值,实现了双线性插值连续化;最后,由于整个网络得训练是端到端的,可采用传统 BP 算法训练。
可变形卷积( Jifeng et al. ICCV 2017) 的特点:
- 卷积核位置参数化;
- 双线性插值连续化;
- 传统 BP 算法训练。

具体而言,上面的左边公式是一个传统卷积,其中 w ( p n ) w(p_n)w(pn) 为卷积核,x ( p 0 + p n ) x(p_0+p_n)x(p0+pn) 为数据,p 0 p_0p0 为中心坐标,p n p_npn 为偏移坐标, p n p_npn属于集合 R RR 中的, R RR 是规则的集合,即 3 × 3 3\times33×3 的格子中。
右边公式为 可变形卷积,其中 w ( p n ) w(p_n)w(pn) 为卷积核, x ( p 0 + p n + Δ p n ) x(p_0+p_n+\Delta p_n)x(p0+pn+Δpn) 为数据, p 0 p_0p0为中心坐标, p n p_npn为标准偏移坐标, Δ p n \Delta p_nΔpn为连续的偏移坐标值,而 Δ p n \Delta p_nΔpn 并不直接学习,是通过学习 G ( q , p ) G(q,p)G(q,p)函数,这样Δ p n \Delta p_nΔpn通过参数化的模块进行学习。参考链接2
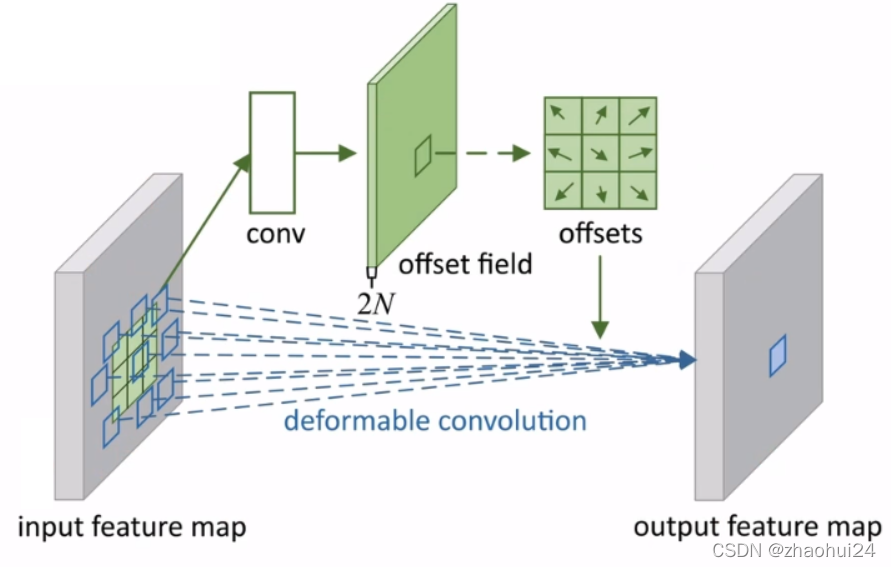
上图中,对于一个输入特征和输出特征之外,它的卷积核的形状是可变的,将某个区域内的数据提取出来,经过一个卷积conv,学习每个卷积核的偏移量,然后将偏移量对应的数据,对原来的特征图进行一个卷积deformable convoluntion,得到最终的结果。
- 此例中,使用了一个 3×3 可变形卷积 (N=9);每个位置对应一个偏置;偏置通过额外卷积学习;每个偏置为二维向量。
2. 谱域图卷积
卷积神经网络在语音、图像、视频取得了巨大成功(尤其是在图像上)。同时,图数据广泛存在于日常生活中,如下所示的几种图数据:
因此,如何将卷积应用在不规则的图数据上,进而更好的处理图数据,经典的卷积网络有一个很明显的局限:无法处理图结构数据。

经典卷积处理图结构数据的局限性
- 只能处理固定输入维度的数据(维数一致性);
- 局部输入数据必须有序(序列有序性)。
- 语音、图像、视频(规则结构)满足以上两点要求。但并不适用于图结构数据(非欧式空间数据)。
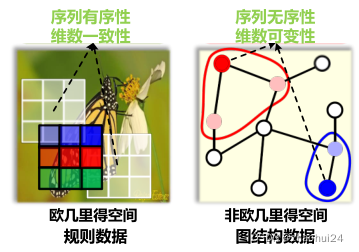
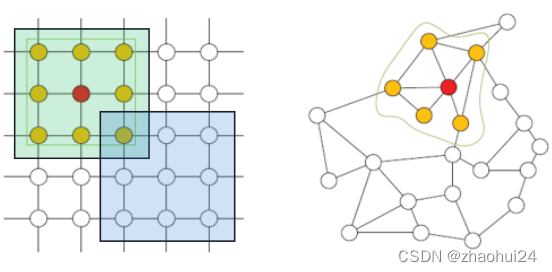
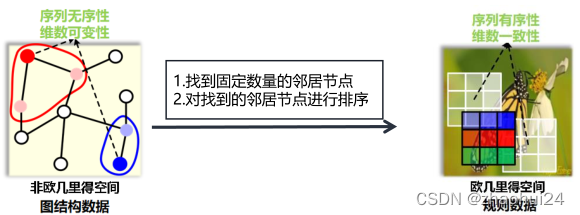
如上图所示,说明了欧式空间的规则数据和非欧空间的图数据最大的两点区别:
- 序列无序性是指:如右图中红色节点的邻居节点有两个,而不知道它们谁应该排在前,谁应该排在后,这就是序列无序性。
- 维数可变性是指:右图中红色节点和蓝色节点的邻居节点个数是可以不相同的,这就是维数可变性。
因此无法将 3 × 3 3\times33×3 的卷积核应用到图数据上,这就是图卷积网络需要解决的问题。
那么如何将卷积操作扩展到图结构数据中?
2.1 图卷积实现
目前图卷积的实现,分为两大类:
1️⃣ 谱域图卷积:
- 根据图谱理论和卷积定理,将数据由空域转换到谱域做处理 ,处理完再转换到空域。
- 有较为坚实的理论基础
基于频谱的方法(Spectral-based)是通过从图信号处理的角度引入滤波器来定义图卷积,其中图卷积运算被解释为从图信号中去除噪声。它的实现思路是根据图谱理论和卷积定理,将数据由空域转换到谱域做处理。参考链接4
2️⃣ 空域图卷积:
- 不依靠 图谱理论 和 卷积定理 ,直接在空间上定义卷积操作 。
- 定义直观 ,灵活性更强 。
基于空间的方法(Spatial based)继承了循环神经网络的思想,通过信息传播来定义图的卷积。
根据卷积定理,两信号在空域(或时域)的卷积的傅里叶变换等于这两个信号在频域中的傅里叶变换的乘积:
F [ f 1 ( t ) ⋆ f 2 ( t ) ] = F 1 ( w ) ⋅ F 2 ( w ) \mathcal{F}\left[f_{1}(t) \star f_{2}(t)\right]=F_{1}(w) \cdot F_{2}(w)F[f1(t)⋆f2(t)]=F1(w)⋅F2(w)
f ( t ) f(t)f(t) 为空域上的信号, F ( w ) F(w)F(w) 为频域上的信号。F \mathcal{F}F 为傅里叶变换,⋆ \star⋆ 表示卷积,⋅ \cdot⋅ 为乘积。
也可以通过反变换的形式来表达:
f 1 ( t ) ⋆ f 2 ( t ) = F − 1 [ F 1 ( w ) ⋅ F 2 ( w ) ] f_{1}(t) \star f_{2}(t)=\mathcal{F^{-1}}\left[F_{1}(w) \cdot F_{2}(w)\right]f1(t)⋆f2(t)=F−1[F1(w)⋅F2(w)]
F − 1 \mathcal{F^{-1}}F−1 为傅里叶反变换。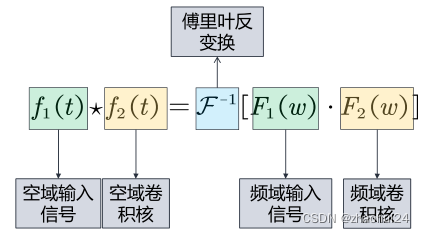
卷积操作的意义如下:
- 将空域信号转换到频域,然后相乘。
- 将相乘的结果再转换到空域。
具体来说,f 1 ( t ) f_1(t)f1(t) 定义为空域输入信号,f 2 ( t ) f_2(t)f2(t)定义为空域卷积核,那么卷积操作就可以这样定义:首先将空域上的信号f 1 ( t ) f_1(t)f1(t) 转换到频域信号 F 1 ( w ) F_1(w)F1(w),f 2 ( t ) f_2(t)f2(t) 转换到频域 F 2 ( w ) F_2(w)F2(w),然后将频域信号相乘,再将相乘后的结果通过傅里叶反变换转回空域,这就是 谱域图卷积的实现思路(将空域转换到频域上处理,处理完再返回空域)。
那么为什么要这样转换呢?为什么要将空域上的信号转换到频域上处理,最后再转回到空域?
经典的卷积操作具有序列有序性和维数不变性的限制,使得经典卷积难以处理图数据,也就是说对于一个3x3的卷积核,它的形状是固定的,它的感受野的中心节点必须要有固定的邻域大小才能使用卷积核,但是图上的节点的邻域节点是不确定的,此外图上节点的邻域节点也是没有顺序的,这就不能直接在空域使用经典的卷积。但是当我们把数据从空域转换到频域,在频域处理数据时,只需要将每个频域的分量放大或者缩小就可以了,不需要考虑信号在空域上存在的问题,这个就是谱域图卷积的巧妙之处。
那么如何转换呢?→ \rightarrow→ 傅里叶变换。
经典傅里叶变换:
x ( t ) = 1 n ∑ w = 0 n − 1 e i 2 π n t w X ( w ) x(t)=\frac{1}{n} \sum_{w=0}^{n-1} e^{i \frac{2 \pi}{n} t w} X(w)x(t)=n1w=0∑n−1ein2πtwX(w)
基于图谱理论,图傅里叶变换:
x ( i ) = ∑ l = 1 n x ^ ( λ l ) u l ( i ) x(i)=\sum_{l=1}^{n} \hat{x}\left(\lambda_{l}\right) u_{l}(i)x(i)=l=1∑nx^(λl)ul(i)
2.2 拉普拉斯矩阵
拉普拉斯矩阵定义: wiki-Laplacian matrix 解释
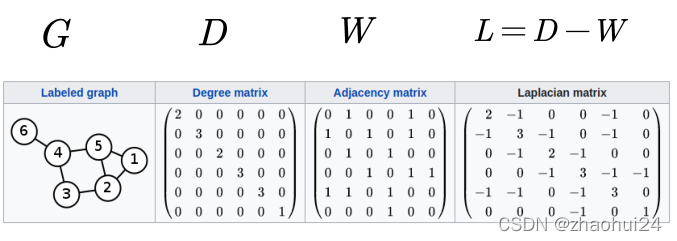
无向图:G = ( v , ε , w ) \mathcal{G} = (v,\varepsilon ,w)G=(v,ε,w),∣ v ∣ = n |v| = n∣v∣=n
邻接矩阵: W ∈ R n × n W \in {\mathbb{R}^{n \times n}}W∈Rn×n
度矩阵: D i i = ∑ j W i j {D_{ii}} = \sum\limits_j {{W_{ij}}}Dii=j∑Wij,D ∈ R n × n D \in {\mathbb{R}^{n \times n}}D∈Rn×n
其中, v vv 代表所有节点的集合(共n nn个),ε \varepsilonε 代表所有边的集合;W WW 代表邻接矩阵(n × n n\times nn×n 的方阵); D DD 为度矩阵,定义为从 i ii 节点出发的所有边的权重之和(为 n × n n\times nn×n 的对角矩阵)。
1️⃣ 拉普拉斯矩阵是对称半正定矩阵。
- 半正定的证明,对任意向量 [ f 1 , f 2 , . . . , f n ] T [f_1,f_2,...,f_n]^{T}[f1,f2,...,fn]T 有
f T L f = f T D f − f T W f = ∑ i = 1 n d i f i 2 − ∑ i , j = 1 n f i f j W i j = 1 2 ( ∑ i = 1 n d i f i 2 − 2 ∑ i , j = 1 n f i f j W i j + ∑ j = 1 n d j f j 2 ) = 1 2 ( ∑ i , j = 1 n W i j ( f i − f j ) 2 ) ≥ 0 \begin{aligned} f^{T} L f &=f^{T} D f-f^{T} W f=\sum_{i=1}^{n} d_{i} f_{i}^{2}-\sum_{i, j=1}^{n} f_{i} f_{j} W_{i j} \\ &=\frac{1}{2}\left(\sum_{i=1}^{n} d_{i} f_{i}^{2}-2 \sum_{i, j=1}^{n} f_{i} f_{j} W_{i j}+\sum_{j=1}^{n} d_{j} f_{j}^{2}\right) \\ &=\frac{1}{2}\left(\sum_{i, j=1}^{n} W_{i j}\left(f_{i}-f_{j}\right)^{2}\right) \geq 0 \end{aligned}fTLf=fTDf−fTWf=i=1∑ndifi2−i,j=1∑nfifjWij=21(i=1∑ndifi2−2i,j=1∑nfifjWij+j=1∑ndjfj2)=21(i,j=1∑nWij(fi−fj)2)≥0
作为对称半正定矩阵,拉普拉斯矩阵有如下性质:
- n 阶对称矩阵一定有 n 个线性无关的特征向量。(对称矩阵性质)
- n 维线性空间中的 n 个线性无关的向量都可以构成它的一组基(矩阵论知识)。
- 拉普拉斯矩阵的 n 个特征向量是线性无关的,它们是 n 维空间中的一组基。
- 下图中,在二维空间中有 u ⃗ 1 \vec u_1u1 , u ⃗ 2 \vec u_2u2 两个线性无关的向量,则它们可以表示这个二维空间中的所有向量,它们就是二维空间中的一组基。

- 下图中,在二维空间中有 u ⃗ 1 \vec u_1u1 , u ⃗ 2 \vec u_2u2 两个线性无关的向量,则它们可以表示这个二维空间中的所有向量,它们就是二维空间中的一组基。
- 对称矩阵的不同特征值对应的特征向量相互正交,这些正交的特征向量构成的矩阵为正交矩阵(对称矩阵性质)。
- 拉普拉斯矩阵的 n 个特征向量是 n 维空间中的一组标准正交基。
- 正交矩阵: U U T = I UU^T=IUUT=I, L = U Λ U − 1 = U Λ U T L=U\Lambda U^{-1}=U\Lambda U^TL=UΛU−1=UΛUT

- 实对称矩阵的特征向量一定是实向量
- 半正定矩阵的特征值一定非负。
- 拉普拉斯矩阵是图上的一种拉普拉斯算子。[下面2.2.2章解释]
以上证明了 拉普拉斯矩阵特征分解后的特征向量不但是 n 维空间中的一组基,而且还是正交的(相乘为0),简称标准正交基。
拉普拉斯矩阵有了上面的性质,就可以进行拉普拉斯矩阵的谱分解了。
2️⃣ 拉普拉斯矩阵的谱分解
特征分解(Eigen decomposition),又称谱分解(Spectral decomposition),是将矩阵分解为由其 特征值 和 特征向量 表示的 矩阵之积 的方法。
L = U Λ U − 1 = U [ λ 1 ⋱ λ n ] U − 1 U = ( u ⃗ 1 , u ⃗ 2 , ⋯ , u ⃗ n ) . u ⃗ i ∈ R n , i = 1 , 2 , ⋯ n \begin{aligned} &L=U \Lambda U^{-1}=U\left[\begin{array}{lll} \lambda_{1} & & \\ & \ddots & \\ & & \lambda_{n} \end{array}\right] U^{-1} \\ \\ &U=\left(\vec{u}_{1}, \vec{u}_{2}, \cdots, \vec{u}_{n}\right). \qquad \vec{u}_{i} \in \mathbb{R}^{n}, i=1,2, \cdots n \end{aligned}L=UΛU−1=U⎣⎡λ1⋱λn⎦⎤U−1U=(u1,u2,⋯,un).ui∈Rn,i=1,2,⋯n
拉普拉斯矩阵又为正交矩阵,有
L = U Λ U − 1 = U Λ U T . ( U U T = I ) L=U\Lambda U^{-1}=U\Lambda U^T . \qquad (UU^T=I)L=UΛU−1=UΛUT.(UUT=I)
为什么拉普拉斯矩阵可以是度矩阵 减 邻接矩阵 L = D − W L=D-WL=D−W 呢?
- 原因是拉普拉斯矩阵是图上的一种拉普拉斯算子。
2.2.1 拉普拉斯算子
wiki-拉普拉斯算子
拉普拉斯算子是 n 维欧几里德空间中的一个二阶微分算子,定义为梯度(∇ f \nabla f∇f)的散度(∇ ⋅ f \nabla \cdot f∇⋅f)。因此如果 f ff 是二阶可微的实函数,则 f ff 的拉普拉斯算子定义为:
Δ f = ∇ ⋅ ( ∇ f ) = d i v ( g r a d ( f ) ) \Delta f=\nabla \cdot (\nabla f)=div(grad(f))Δf=∇⋅(∇f)=div(grad(f))
对于 n 维欧几里得空间,可以认为拉普拉斯算子是一个二阶微分算子,即在各个维度求二阶导数后求和。
Δ f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}Δf=∂x2∂2f+∂y2∂2f
在三维欧几里得空间,对于一个三元函数 f ( x , y , z ) f(x,y,z)f(x,y,z) ,可以得到:
Δ f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 + ∂ 2 f ∂ z 2 \Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}+\frac{\partial^{2} f}{\partial z^{2}}Δf=∂x2∂2f+∂y2∂2f+∂z2∂2f
2️⃣离散情况下欧氏空间的拉普拉斯算子
离散函数的一阶导数为:
∂ f ∂ x = f ′ ( x ) = f ( x + 1 ) − f ( x ) \frac{\partial f}{\partial x}=f^\prime (x)=f(x+1)-f(x)∂x∂f=f′(x)=f(x+1)−f(x)
离散函数的二阶导数为:
∂ 2 f ∂ x 2 = f ′ ′ ( x ) = f ′ ( x + 1 ) − f ′ ( x ) = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \frac{\partial^2 f}{\partial x^2}=f^{\prime \prime}(x)=f^\prime (x+1)-f^\prime (x)=f(x+1)+f(x-1)-2f(x)∂x2∂2f=f′′(x)=f′(x+1)−f′(x)=f(x+1)+f(x−1)−2f(x)
类似的,对于两个变量的函数(例如下图图像):

在 x xx,y yy 方向有:
∂ 2 f ∂ x 2 = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) ∂ 2 f ∂ y 2 = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) \begin{aligned} &\frac{\partial^{2} f}{\partial x^{2}}=f(x+1, y)+f(x-1, y)-2 f(x, y) \\ \\ &\frac{\partial^{2} f}{\partial y^{2}}=f(x, y+1)+f(x, y-1)-2 f(x, y) \end{aligned}∂x2∂2f=f(x+1,y)+f(x−1,y)−2f(x,y)∂y2∂2f=f(x,y+1)+f(x,y−1)−2f(x,y)
两个变量的离散拉普拉斯算子可以写成:
Δ f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}=f(x+1, y)+f(x-1, y)+f(x, y+1)+f(x, y-1)-4f(x, y)Δf=∂x2∂2f+∂y2∂2f=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
即在欧氏空间内,二维的拉普拉斯算子可以理解为中心节点与周围节点的差值,然后求和。
2.2.2 图上的拉普拉斯算子
图上的拉普拉斯算子可以定义如下:
Δ f i = ∑ ( i , j ) ∈ ϵ ( f i − f j ) \Delta f_i=\sum_{(i,j)\in \epsilon} (f_i-f_j)Δfi=(i,j)∈ϵ∑(fi−fj)
其中,f = ( f 1 , f 2 , . . . , f n ) f=(f_1,f_2,...,f_n)f=(f1,f2,...,fn),代表 n 个节点上每个节点的信号;ϵ \epsilonϵ 代表边集合。
当有权重时:
Δ f i = ∑ ( i , j ) ∈ ϵ W i j ( f i − f j ) \Delta f_i=\sum_{(i,j)\in \epsilon} W_{ij}(f_i-f_j)Δfi=(i,j)∈ϵ∑Wij(fi−fj)
可以理解为中心节点依次减去周围节点,乘以权重后,求和。(i ii 和 j jj 节点之间存在连边)
Δ f i = ∑ ( i , j ) ∈ ϵ W i j ( f i − f j ) = ∑ j = 1 n W i j ( f i − f j ) = D i i f i − ∑ j = 1 n W i j f j \Delta f_i=\sum_{(i,j)\in \epsilon} W_{ij}(f_i-f_j)=\sum_{j=1}^n W_{ij}(f_i-f_j)=D_{ii}f_i-\sum_{j=1}^n W_{ij}f_jΔfi=(i,j)∈ϵ∑Wij(fi−fj)=j=1∑nWij(fi−fj)=Diifi−j=1∑nWijfj
对于 n 个节点,则有
Δ f = g θ = ( Δ f 1 ⋮ Δ f n ) = ( D 11 f 1 − ∑ j = 1 n W 1 j f j ⋮ D n n f n − ∑ j = 1 n W n j f j ) = ( D 11 ⋱ D n n ) f − W f = D f − W f = L f \begin{aligned} \Delta f &=g_{\theta}=\left(\begin{array}{c} \Delta f_{1} \\ \vdots \\ \Delta f_{n} \end{array}\right)=\left(\begin{array}{c} D_{11} f_{1}-\sum_{j=1}^{n} W_{1 j} f_{j} \\ \vdots \\ D_{n n} f_{n}-\sum_{j=1}^{n} W_{n j} f_{j} \end{array}\right) \\ &=\left(\begin{array}{ccc} D_{11} & & \\ & \ddots & \\ & & D_{n n} \end{array}\right) f-W f=D f-W f=L f \end{aligned}Δf=gθ=⎝⎜⎛Δf1⋮Δfn⎠⎟⎞=⎝⎜⎛D11f1−∑j=1nW1jfj⋮Dnnfn−∑j=1nWnjfj⎠⎟⎞=⎝⎛D11⋱Dnn⎠⎞f−Wf=Df−Wf=Lf
因此得出结论:拉普斯矩阵是图上的一种拉普拉斯算子。
《Discrete Regularization Weighted Graphs for Image and Mesh Filtering》,定义了在图上如何做梯度运算和散度运算。
2.3 图傅里叶变换
图上的信号一般表达为一个向量。假设有n个节点,将图上的信号记为:
x = [ x 1 , x 2 , ⋯ , x n ] T ∈ R x=[x_1, x_2,\cdots,x_n]^T \in \mathbb{R}x=[x1,x2,⋯,xn]T∈R
每一个节点上有一个信号值,如下图所示,类似于图像上的像素值。i ii 节点上的值为 x ( i ) = x i x(i)=x_ix(i)=xi 。
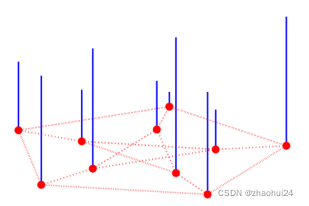
上图中 蓝色线段代表信号的大小,类似于图像上灰度图像像素,像素越高,画的这个线段越长。图上的信号也是类似的,只不过若一个信号有 c cc 个通道,那么 x = [ x 1 , x 2 , . . . , x n ] ∈ R n ∗ c x=[x_1,x_2,...,x_n] \in R^{n*c}x=[x1,x2,...,xn]∈Rn∗c,彩色图像有 R,G,B 三个通道,则 c = 3 c=3c=3。参考链接2
1️⃣ 经典傅里叶变换
傅里叶变换的公式:傅里叶分析-链接
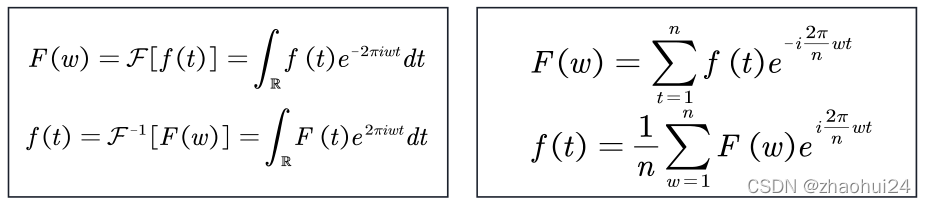
傅里叶变换中不同频率的余弦函数可视为 基函数,其傅里叶系数表示基的振幅。如下图所展示的样子,相位在这个图中被忽略了 ,傅里叶系数实际上包含了振幅和相位。

经典傅里叶变换其实就是说:一个信号由不同频率的基函数信号叠加而成,比如上图中红色信号是原信号,蓝色信号是不同频率上的基函数信号(余弦或者正弦函数)。上图中,红色原信号可以由不同频率的基函数线性组合而成,蓝色的高度表示基前面的系数,也就是所谓的傅里叶系数,也就是原函数在这个基上的坐标分量。
傅里叶反变换的本质是:把任意一个函数表示成了若干正交基函数的线性组合。
傅里叶正变换的本质是:求线性组合系数。具体做法是由原函数和基函数的共轭的内积求得 。
F ( w ) = ∑ t = 1 n f ( t ) e − i 2 π n w t f ( t ) = 1 n ∑ w = 1 n F ( w ) e i 2 π n w t \begin{aligned} &F(w)=\sum_{t=1}^{n} f(t) e^{-i \frac{2 \pi}{n} w t} \\ &f(t)=\frac{1}{n} \sum_{w=1}^{n} F(w) e^{i \frac{2 \pi}{n} w t} \end{aligned}F(w)=t=1∑nf(t)e−in2πwtf(t)=n1w=1∑nF(w)ein2πwt
2️⃣ 图傅里叶变换
傅里叶反变换的本质是:把任意一个函数表示成了若干个正交基函数的线性组合。
f ( t ) = F − 1 [ F ( w ) ] = ∫ R F ( t ) e 2 π i w t d t f ( t ) = 1 n ∑ w = 1 n F ( w ) e i 2 π n w t \begin{aligned} &f(t)=\mathcal{F}^{-1}[F(w)]=\int_{\mathbb{R}} F(t) e^{2 \pi i w t} d t \\ &f(t)=\frac{1}{n} \sum_{w=1}^{n} F(w) e^{i \frac{2 \pi}{n} w t} \end{aligned}f(t)=F−1[F(w)]=∫RF(t)e2πiwtdtf(t)=n1w=1∑nF(w)ein2πwt
上面公式是连续的傅里叶变换,下面是离散的。
对应graph上的信号 x ∈ R x \in \mathbb{R}x∈R,如果要进行一个傅里叶变换,很自然的能想到:找到一组正交基,通过这组正交基的线性组合来表达 x ∈ R x \in \mathbb{R}x∈R。
图傅里叶变换,使用前面提到的拉普拉斯矩阵的特征向量,作为图傅里叶变换的基函数。
U = ( u ⃗ 1 , u ⃗ 2 , ⋯ , u ⃗ n ) U=\left(\vec{u}_{1}, \vec{u}_{2}, \cdots, \vec{u}_{n}\right)U=(u1,u2,⋯,un)
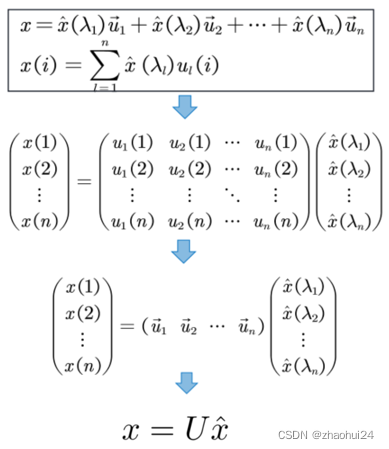
因此,使用拉普拉斯的特征向量作为基函数,任意的图上的信号可以表示为:
x = x ^ ( λ 1 ) u ⃗ 1 + x ^ ( λ 2 ) u ⃗ 2 + ⋯ + x ^ ( λ n ) u ⃗ n x=\hat{x}\left(\lambda_{1}\right) \vec{u}_{1}+\hat{x}\left(\lambda_{2}\right) \vec{u}_{2}+\cdots+\hat{x}\left(\lambda_{n}\right) \vec{u}_{n}x=x^(λ1)u1+x^(λ2)u2+⋯+x^(λn)un
公式中的 x xx 是输入信号, x ^ ( λ 1 ) \hat x(\lambda_1)x^(λ1) 是傅里叶系数。
为什么任意图上的信号 x ∈ R x \in \mathbb{R}x∈R 都可以表示成这样的线性组合?
拉普拉斯矩阵的特征向量 U = ( u ⃗ 1 , u ⃗ 2 , ⋯ , u ⃗ n ) U=\left(\vec{u}_{1}, \vec{u}_{2}, \cdots, \vec{u}_{n}\right)U=(u1,u2,⋯,un) 是 n 维空间中的 n 个线性无关的正交向量。
n 维空间中 n 个线性无关的向量可以构成空间的一组基,而且拉普拉斯矩阵的特征向量还是一组正交基。
3️⃣ 傅里叶反变换
x ^ \hat xx^ 是谱域上的信号。
4️⃣ 傅里叶正变换
傅里叶正变换就是求傅里叶反变换前面的系数,也就是每个基函数前面的振幅。
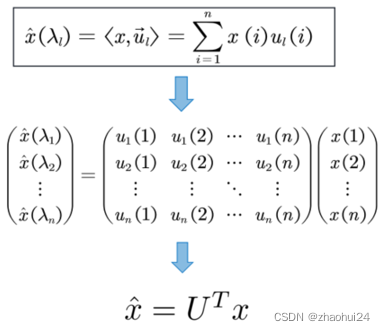
依靠图傅里叶变换,可以将定义在graph节点上的信号 x ∈ R n x\in \mathbb{R_n}x∈Rn 从空间域转 换到谱域。
- 空间域 → \rightarrow→ 谱域 x ^ = U T x ∈ R n \hat x = U^Tx\in \mathbb{R_n}x^=UTx∈Rn
- 谱域 → \rightarrow→ 空间域 x = U x ^ x=U\hat xx=Ux^
其中
L = U Λ U − 1 = U [ λ 1 ⋱ λ n ] U − 1 U = ( u ⃗ 1 , u ⃗ 2 , ⋯ , u ⃗ n ) . u ⃗ i ∈ R n , i = 1 , 2 , ⋯ n \begin{aligned} &L=U \Lambda U^{-1}=U\left[\begin{array}{lll} \lambda_{1} & & \\ & \ddots & \\ & & \lambda_{n} \end{array}\right] U^{-1} \\ \\ &U=\left(\vec{u}_{1}, \vec{u}_{2}, \cdots, \vec{u}_{n}\right). \qquad \vec{u}_{i} \in \mathbb{R}^{n}, i=1,2, \cdots n \end{aligned}L=UΛU−1=U⎣⎡λ1⋱λn⎦⎤U−1U=(u1,u2,⋯,un).ui∈Rn,i=1,2,⋯n
5️⃣ 经典傅里叶变换与图傅里叶变换对比

| 经典傅里叶变换 | 图傅里叶变换 | |
|---|---|---|
| F ( w ) = ∫ R f ( t ) e − 2 π i w t d t F(w)=\int_{\mathbb{R}} f(t) e^{-2 \pi i w t} d tF(w)=∫Rf(t)e−2πiwtdt(连续) X ( w ) = ∑ t = 1 n e − i 2 π n w t x ( t ) X(w)=\sum_{t=1}^{n} e^{-i \frac{2 \pi}{n} w t}x(t)X(w)=∑t=1ne−in2πwtx(t)(离散) | x ^ ( λ l ) = ∑ i = 1 n x ( i ) u l ( i ) \hat x(\lambda_l)= \sum_{i=1}^{n} x(i)u_l(i)x^(λl)=∑i=1nx(i)ul(i) | |
| 基 | e 2 π i w t e^{2 \pi i w t}e2πiwt(连续),e i 2 π n w t e^{i \frac{2 \pi}{n} w t}ein2πwt(离散) | u ⃗ l \vec u_lul |
| 频率 | w ww | λ l \lambda_lλl |
| 分量的振幅 | F ( w ) F(w)F(w) | x ^ ( λ l ) \hat x(\lambda_l)x^(λl) |
为什么基函数一个有共轭,一个没有?
- 实数拉普拉斯矩阵的特征向量一定是实向量。共轭之后还是自身。
为什么使用拉普拉斯的特征向量作为基?
- 经典傅里叶变换有如下规律:傅里叶变换的基函数是拉普拉斯算子的本征函数。
− Δ ( e 2 π i ξ t ) = − ∂ 2 ∂ t 2 e 2 π i ξ t = ( 2 π ξ ) 2 e 2 π i ξ t -\Delta\left(e^{2 \pi i \xi t}\right)=-\frac{\partial^{2}}{\partial t^{2}} e^{2 \pi i \xi t}=(2 \pi \xi)^{2} e^{2 \pi i \xi t}−Δ(e2πiξt)=−∂t2∂2e2πiξt=(2πξ)2e2πiξt - 又因为拉普拉斯矩阵就是图上的拉普拉斯算子。所以,类似的,图傅里叶变换的基函数即为图拉普拉斯矩阵的特征向量。
L u ⃗ l = λ l u ⃗ l L\vec u_l=\lambda_l \vec u_lLul=λlul
- 经典傅里叶变换有如下规律:傅里叶变换的基函数是拉普拉斯算子的本征函数。
本征函数和本征向量可以认为是特征值和特征向量的扩展。特征向量是针对矩阵而言,而本征向量是针对算子而言的,很接近,宽泛一点可以认为是一个概念。
2.3.1 特征向量基的性质
拉普拉斯矩阵的特征值担任了和频率类似的位置。
- 拉普拉斯的特征值都是非负的。且最小特征值为0。类似于经典傅里叶变换中的常数值(可视为频率为0)
拉普拉斯矩阵的特征向量担任了基函数的位置。
- 0 特征值对应一个常数特征向量,这个和经典傅里叶变换中的常数项类似。
- 低特征值 对应的特征向量比较平滑,高特征值 对应的特征向量变换比较剧烈。两者对应于 低频基函数 和 高频基函数。

上图是三个不同的特征值对应的特征向量的示例,u 1 u_1u1 是最小的特征值对应的特征向量(可以看出很平滑), u 2 u_2u2 是第二小的特征值对应的特征向量(不太平滑),u 50 u_{50}u50 是第五十小的特征值对应的特征向量(很不平滑)。
- 通过Zero crossing 函数来认识特征向量基。

Zero crossing 是指有边相邻的两个节点上对应的值一个大于0,一个小于0,每出现这样的一条边,Zero crossing就加一,通过Zero crossing的个数可以粗略的判断信号的震荡程度,或者可以说是平滑程度。从右图可以看到,大特征值可以视为高频信号,小特征值可以视为低频信号。
- 通过定义图拉普拉斯二次型(graph Laplacian quadratic form)来定义信号的 平滑程度。其表示有边相连的两个节点信号的平方差乘以边的权重后求和。其值越小,代表信号 x xx 越平滑:
x T L x = 1 / 2 ∑ i , j = 1 m W i , j ( x ( i ) − x ( j ) ) 2 u ⃗ l T L u ⃗ l = λ l \begin{aligned} &x^{T} L x=1 / 2 \sum_{i, j=1}^{m} W_{i, j}(x(i)-x(j))^{2} \\ &{\vec u_l}^TL\vec u_l=\lambda_l \end{aligned}xTLx=1/2i,j=1∑mWi,j(x(i)−x(j))2ulTLul=λl
当特征向量带入这个函数时,二次型的值等于特征值。这恰好是符合经典傅里叶变换中的频率设定——频率越高,基函数(余弦函数)变化越陡峭。
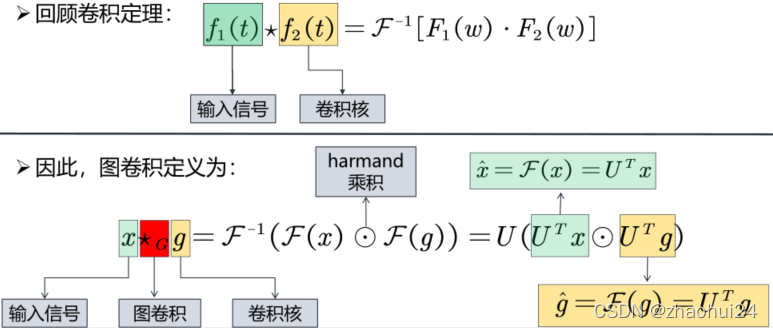
图上的卷积定义:先对F ( x ) F(x )F(x) 和 F ( g ) F ( g )F(g) 做傅里叶正变换,然后在谱域上做 h a r m a n d harmandharmand 乘积,也就是 F ( x ) ⊙ F ( g ) F(x) \odot F(g)F(x)⊙F(g) ,最后通过傅里叶反变换 F − 1 \mathcal{F^{-1}}F−1 将结果返回到空域。前面讲了傅里叶正变换就是 x ^ = U T x \hat x=U^Txx^=UTx , 则傅里叶反变换就是U ( U T x ⊙ U T g ) U(U^Tx \odot U^Tg)U(UTx⊙UTg) 。
将两信号分别视为 输入信号 和 卷积核,那么卷积操作可以定义为
- 将空域信号转换到频域,然后相乘。
- 将相乘的结果再转换到空域。

如果以矩阵乘法的形式表达这个公式,去掉 h a r m a n d harmandharmand 乘积[两个矩阵对应位置元素相乘]。同时,通常并不关心空间域上的滤波器信号 g gg 是什么样子的,只关心其在频率域的情况。令 g θ = d i a g ( U T g ) g_{\theta}=diag(U^Tg)gθ=diag(UTg),公式等价的转换成下式:
x ⋆ G g θ = U g θ U T x = U ( g ^ ( λ 1 ) ⋱ g ^ ( λ n ) ) ( x ^ ( λ 1 ) x ^ ( λ 2 ) ⋮ x ^ ( λ n ) ) = U ( g ^ ( λ 1 ) ⋱ g ^ ( λ n ) ) U T x x \star_{G} g_{\theta}=U g_{\theta} U^{T} x=U\left(\begin{array}{ccc} \hat{g}\left(\lambda_{1}\right) & & \\ & \ddots & \\ & & \hat{g}\left(\lambda_{n}\right) \end{array}\right)\left(\begin{array}{c} \hat{x}\left(\lambda_{1}\right) \\ \hat{x}\left(\lambda_{2}\right) \\ \vdots \\ \hat{x}\left(\lambda_{n}\right) \end{array}\right)=U\left(\begin{array}{ccc} \hat{g}\left(\lambda_{1}\right) & & \\ & \ddots & \\ & & \hat{g}\left(\lambda_{n}\right) \end{array}\right) U^{T} xx⋆Ggθ=UgθUTx=U⎝⎛g^(λ1)⋱g^(λn)⎠⎞⎝⎜⎜⎜⎛x^(λ1)x^(λ2)⋮x^(λn)⎠⎟⎟⎟⎞=U⎝⎛g^(λ1)⋱g^(λn)⎠⎞UTx
上面就是谱域图卷积最终的公式,所有的谱域图卷积的原理就是这个公式,只是对滤波器 g ^ \hat gg^ 做了不同的处理。这个公式的意义是:卷积核信号(或者说滤波器信号) g ^ \hat gg^ 也是一个 n 维的向量,它的作用是将原信号的不同的分量进行一个放大或者缩小,这取决于卷积核信号在谱域上不同元素的值。
2.4 图谱卷积模型
三个图谱卷积模型(SCNN、ChebNet、GCN)均立足于图谱理论且一脉相承,ChebNet可看做SCNN的改进,GCN可看做ChebNet的改进,三个模型均可认为是上面x ⋆ G g θ = U g θ U T x = ⋯ x \star_{G} g_{\theta} =U g_{\theta} U^{T} x=\cdotsx⋆Ggθ=UgθUTx=⋯ 式子的一个特例。
| SCNN | ChebNet | GCN |
|---|---|---|
| 用可学习的对角矩阵来代替谱域的卷积核 | 用Chebyshev 多项式代替谱域的卷积核 | GCN可以视为ChebNet 的进一步简化。仅考虑1阶切比雪夫多项式,且每个卷积核仅只有一个参数 |
| x ⋆ G g θ = U F U T x x \star_{G} g_{\theta}=UFU^{T} xx⋆Ggθ=UFUTx | x ⋆ G g θ = U g θ U T x = ∑ k = 0 K β k T k ( L ^ ) x x \star_{G} g_{\theta}=U g_{\theta} U^{T} x=\sum_{k=0}^K \beta_k T_k(\hat L)xx⋆Ggθ=UgθUTx=k=0∑KβkTk(L^)x | x ⋆ G g θ = θ ( D ~ − 1 / 2 W ~ D ~ − 1 / 2 ) x x \star_{G} g_{\theta}=\theta (\tilde D^{-1 / 2} \tilde W \tilde D^{-1 / 2})xx⋆Ggθ=θ(D~−1/2W~D~−1/2)x |
2.4.1 SCNN
论文解读一代GCN《Spectral Networks and Locally Connected Networks on Graphs》- 参考链接
卷积前后每个节点的信号是什么?
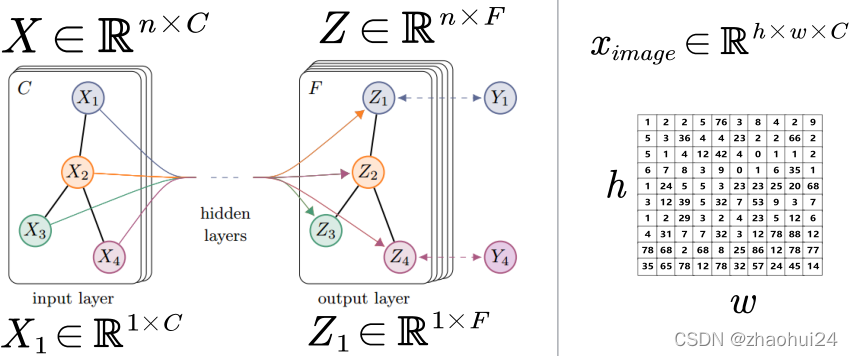
上图片是GCN模型的图片,因为不同方法的卷积网络特征图的规律都是一样的。如上面左图,首先某一层的图的信号可以表示为一个 n × C n\times Cn×C 的一个矩阵, n nn 就表示有 n 个不同的节点, C CC 代表通道个数。图上的信号可以分解为各个节点上的信号,用 X XX 表示整个图上的信号,是一个 n × C n\times Cn×C 的矩阵,具体如 X 1 X_1X1 这个节点它就是一个 1 × C 1\times C1×C 的向量,有 n 个节点,就是一个 n × C n\times Cn×C 的矩阵。当假设通道 C = 1 C=1C=1 时,整个图上的信号其实就类似于灰度图像上的信号。
这种表示和 image 上的表示是一样的,如上面右图,假设一张图片的高是 h hh ,宽是 w ww,通常我们使用 h × w × C h\times w\times Ch×w×C 的矩阵来代表图像某一层的特征图。如上面中间图,特征图的形式是 n × F n\times Fn×F, F FF 表示该层的一个特征图的通道数。
上图是在说明图卷积网络不同层的特征图,它们共享一个图的结构,传播到下一层,图的结构是不变的(节点个数不变,节点之间的关系不变),变的是图上的信号或者说是节点上的信号。如 X 1 X_1X1 在 i n p u t inputinput l a y e r layerlayer 层是一个 1 × C 1\times C1×C 的向量,而到了 o u t p u t outputoutput l a y e r layerlayer 层变成一个 1 × F 1\times F1×F 的向量,通道个数也变了。
SCNN 核心思想:
用可学习的对角矩阵来代替谱域的卷积核,从而实现图卷积操作。
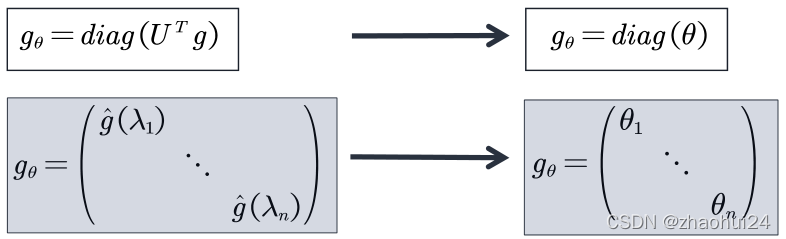
上面的卷积核,由于它只有主对角线上的元素是非零的,所以这个矩阵只有 n nn 个值,SCNN 的思想就是用 n nn个可学习的参数,来替换谱域的卷积核。这样就可以定义卷积了。
- 具体的卷积公式定义如下:
x k + 1 , j = h ( U ∑ i = 1 C k − 1 F k , i , j U T x k , i ) ( j = 1 ⋯ C k ) F k , i , j = ( θ 1 ⋱ θ n ) x_{k+1, j}=h\left(U \sum_{i=1}^{C_{k-1}} F_{k, i , j} U^{T} x_{k, i}\right)\left(j=1 \cdots C_{k}\right) \quad F_{k, i, j}=\left(\begin{array}{lll} \theta_{1} & & \\ & \ddots & \\ & & \theta_{n} \end{array}\right)xk+1,j=h(Ui=1∑Ck−1Fk,i,jUTxk,i)(j=1⋯Ck)Fk,i,j=⎝⎛θ1⋱θn⎠⎞
其中 C k C_kCk 表示第 k 层的 channel 个数; x k , i ∈ R n x_{k,i}\in \mathbb{R}^nxk,i∈Rn表示第 k层的第 i ii 个 channel 的 feature map。 F k , i , j ∈ R n ∗ n F_{k,i,j}\in \mathbb{R}^{n*n}Fk,i,j∈Rn∗n 代表参数化的谱域的卷积核矩阵,它是一个对角矩阵,包含了 n 个可学习的参数; U UU 是拉普拉斯矩阵 L LL 特征分解之后的特征向量; h ( ⋅ ) h(\cdot)h(⋅) 是激活函数。
假设输入channel 和输出channel 为1,也就是每个节点的特征为1。简化版的SCNN卷积公式如下:
x k + 1 = h ( U F k U T x k ) x k + 1 ∈ R n , x k ∈ R n x_{k+1}=h\left(U F_{k} U^{T} x_{k}\right) \quad x_{k+1} \in \mathbb{R}^{n}, x_{k} \in \mathbb{R}^{n}xk+1=h(UFkUTxk)xk+1∈Rn,xk∈Rn
这和经典信号处理的频率滤波比较类似,分三步:
空间域 → \rightarrow→ 谱域 U T x k U^Tx_kUTxk
对每个“频率分量”放大或者缩小:F k U T x k F_kU^Tx_kFkUTxk ; F k = ( θ 1 ⋱ θ n ) F_{k}=\left(\begin{array}{lll} \theta_{1} & & \\ & \ddots & \\ & & \theta_{n} \end{array}\right)Fk=⎝⎛θ1⋱θn⎠⎞,参数θ \thetaθ是可学习的
谱域 → \rightarrow→ 空间域 x = U x ^ x=U\hat xx=Ux^
上面这种形式和前面的图卷积的表达比较类似,首先 U T x k U^Tx_kUTxk 实际上是一个图傅里叶正变换,将信号从空间域转换到谱域;然后由 F k U T x k F_kU^Tx_kFkUTxk 也就是 n nn 个可学习的参数,替换原来谱域的卷积核,每个θ \thetaθ 实际上是对每个频率分量进行放大或者缩小;最后再用 U UU 乘以整个谱域调整后的信号,再将其转换为空间域。
公式得主要思想是将谱域的卷积核变成了一个可学习的谱域的卷积核,然后就会有 n nn 个可学习的参数。
SCNN 实际上是第一个将理论转换为实践的模型,但有很多的缺点:
计算拉普拉斯矩阵的特征值分解非常耗时。
- 计算复杂度为 O ( n 3 ) O(n^3)O(n3),n nn 为节点个数。当处理大规模图数据时(比如社交网络数据,通常有上百万个节点)会面临很大的挑战。
模型的参数复杂度较大。
- 计算复杂度为 O ( n ) O(n)O(n),当节点数较多时容易过拟合。
无法保证局部链接。
无法保证局部连接是因为SCNN转换到空域时,实际上是一个全连接的形式,这个和经典卷积是违背的。
2.4.2 ChebNet
《Convolutional neural networks on graphs with fast localized spectral filtering》- NIPS 2016
ChebNet 核心思想:为了解决SCNN的缺点,ChebNet采用Chebyshev(切比雪夫)多项式代替谱域的卷积核。
- 第一类切比雪夫多项式由以下递推关系确定
- T 0 ( x ) = 1 {\displaystyle T_{0}(x)=1}T0(x)=1
T 1 ( x ) = x {\displaystyle T_{1}(x)=x}T1(x)=x
T n + 1 ( x ) = 2 x T n ( x ) − T n − 1 ( x ) {\displaystyle T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x)}Tn+1(x)=2xTn(x)−Tn−1(x) ,( n = 1 , 2 , ⋯ ) (n=1,2,\cdots)(n=1,2,⋯)
- T 0 ( x ) = 1 {\displaystyle T_{0}(x)=1}T0(x)=1
切比雪夫多项式 0 阶的切比雪夫多项式是1,一阶的是 x xx,依此类推,高阶的切比雪夫多项式有这样的规律: T N + 1 ( x ) = 2 x T n ( x ) − T n − 1 ( x ) T_{N+1}(x)=2xT_{n}(x)-T_{n-1}(x)TN+1(x)=2xTn(x)−Tn−1(x) ,( n = 1 , 2 , . . . ) (n = 1,2,...)(n=1,2,...)。若把 x xx 换成矩阵之后,就成了矩阵形式的切比雪夫多项式,如下面,把 x xx 换成了拉普拉斯矩阵 L LL:
T 0 ( L ) = I {\displaystyle T_{0}(L)=I}T0(L)=I
T 1 ( L ) = L {\displaystyle T_{1}(L)=L}T1(L)=L
T n + 1 ( L ) = 2 L T n ( L ) − T n − 1 ( L ) {\displaystyle T_{n+1}(L)=2LT_{n}(L)-T_{n-1}(L)}Tn+1(L)=2LTn(L)−Tn−1(L)
切比雪夫多项式在 逼近理论 中有重要的应用,因为切比雪夫多项式可以用于多项式插值,相应的插值多项式能最大限度地降低 龙格现象,并且提供多项式在连续函数的最佳一致逼近,也就是说可以用切比雪夫多项式来逼近函数进行多项式插值。
以前的做法是将 x 0 , x 1 , x 2 , . . . , x K x^0, x^1, x^2,...,x^Kx0,x1,x2,...,xK作为基,进行多项式插值,来学习系数 β 0 , β 1 , . . . \beta_0,\beta_1,...β0,β1,...

ChebNet 方法认为谱域的卷积核的取值是一个与特征值相关的函数,可以用切比雪夫多项式来逼近这个函数。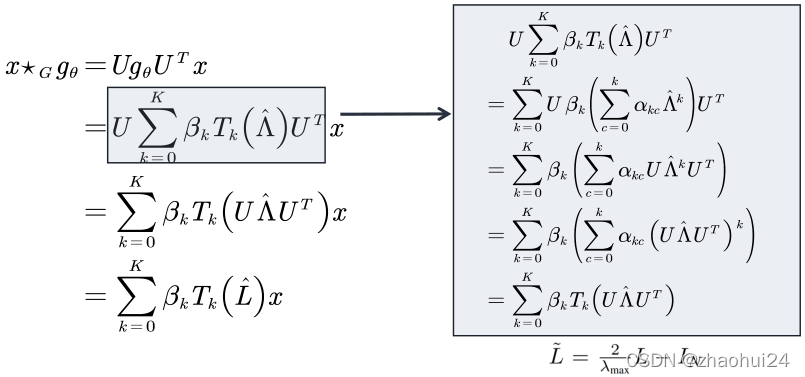
g θ g_{\theta}gθ 是谱域的卷积核,用一个切比雪夫多项式插值来逼近它,只需要学习前面的系数 β k \beta_kβk 就可以了,然后就能推导出最下面的结果。这样做的好处是 不需要求拉普拉斯矩阵的特征向量 U UU ,直接使用拉普拉斯矩阵,时间复杂度大大降低。下面公式就是ChebNet 方法的最终公式:
x ⋆ G g θ = U g θ U T x = ∑ k = 0 K β k T k ( L ^ ) x x \star_{G} g_{\theta}=U g_{\theta} U^{T} x=\sum_{k=0}^K \beta_k T_k(\hat L)xx⋆Ggθ=UgθUTx=k=0∑KβkTk(L^)x
ChebNet 优点:
卷积核只有 K+1 个可学习的参数,一般 K 远小于 n,参数的复杂度被大大降低;
采用Chebyshev多项式代替谱域的卷积核后,经过公式推导,ChebNet 不需要对拉普拉斯矩阵做特征分解了,省略了最耗时的步骤。
卷积核具有严格的空间局部性。同时,K 就是卷积核的“感受野半径”。即将中心顶点 K 阶近邻节点作为邻域节点。
2.4.3 GCN
《SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》
GCN 核心思想:
GCN 可以视为对 ChebNet 的进一步简化。仅仅考虑 一 阶切比雪夫多项式,且每个卷积核仅仅只有一个参数。
x ⋆ G g θ = ∑ k = 0 K β k T k ( L ^ ) x = ∑ k = 0 1 β k T k ( L ^ ) x = β 0 T 0 ( L ^ ) x + β 1 T 1 ( L ^ ) x = ( β 0 + β 1 L ^ ) x = ( β 0 + β 1 ( L − I n ) ) x = ( β 0 − β 1 ( D − 1 / 2 W D − 1 / 2 ) ) x \begin{aligned} x \star_{G} g_{\theta} &=\sum_{k=0}^{K} \beta_{k} T_{k}(\hat{L}) x=\sum_{k=0}^{1} \beta_{k} T_{k}(\hat{L}) x \\ &=\beta_{0} T_{0}(\hat{L}) x+\beta_{1} T_{1}(\hat{L}) x \\ &=\left(\beta_{0}+\beta_{1} \hat{L}\right) x \\ &=\left(\beta_{0}+\beta_{1}\left(L-I_{n}\right)\right) x \\ &=\left(\beta_{0}-\beta_{1}\left(D^{-1 / 2} W D^{-1 / 2}\right)\right) x \end{aligned}x⋆Ggθ=k=0∑KβkTk(L^)x=k=0∑1βkTk(L^)x=β0T0(L^)x+β1T1(L^)x=(β0+β1L^)x=(β0+β1(L−In))x=(β0−β1(D−1/2WD−1/2))x
其中 W WW 是邻接矩阵; D DD 是度矩阵;
T 0 ( L ^ ) = I , T 1 ( L ^ ) = L ^ L ^ = 2 λ max L − I n λ max = 2 L = I n − D − 1 / 2 W D − 1 / 2 \begin{aligned} &T_{0}(\hat{L})=I, \qquad T_{1}(\hat{L})=\hat{L} \\ &\hat{L}=\frac{2}{\lambda_{\max }} L-I_{n} \\ &\lambda_{\max }=2 \\ &L=I_{n}-D^{-1 / 2} W D^{-1 / 2} \end{aligned}T0(L^)=I,T1(L^)=L^L^=λmax2L−Inλmax=2L=In−D−1/2WD−1/2
ChebNet中卷积核 K + 1 K+1K+1 个可学习的参数,GCN中设置 K = 1 K=1K=1,每个卷积核 2 个可学习的参数。进一步简化,使每个卷积核只有1个可学习的参数
- 令:β 0 = − β 1 = θ \beta _0= - \beta_1=\thetaβ0=−β1=θ
- 那么
x ⋆ G g θ = ( β 0 − β 1 ( D − 1 / 2 W D − 1 / 2 ) ) x = ( θ ( D − 1 / 2 W D − 1 / 2 + I n ) ) x x \star_{G} g_{\theta}=\left(\beta_{0}-\beta_{1}\left(D^{-1 / 2} W D^{-1 / 2}\right)\right) x=\left(\theta\left(D^{-1 / 2} W D^{-1 / 2}+I_{n}\right)\right) xx⋆Ggθ=(β0−β1(D−1/2WD−1/2))x=(θ(D−1/2WD−1/2+In))x
renormalization trick
因为 D − 1 / 2 W D − 1 / 2 + I n D^{-1 / 2} W D^{-1 / 2}+I_nD−1/2WD−1/2+In 有范围 [ 0 , 2 ] [0,2][0,2] 的特征值,如果在深度神经网络模型中使用该算子,则反复应用该算子会导致数值不稳定(发散)和梯度爆炸/消失,为了解决这个问题,引入了一个renormalization trick。
- 将 D − 1 / 2 W D − 1 / 2 + I n → D ~ − 1 / 2 W ~ D ~ − 1 / 2 D^{-1 / 2} W D^{-1 / 2}+I_n \quad \rightarrow \quad \tilde D^{-1 / 2} \tilde W \tilde D^{-1 / 2}D−1/2WD−1/2+In→D~−1/2W~D~−1/2
- 缔造了新的 W ~ = W + I n \tilde W=W+I_nW~=W+In,D ~ i i = ∑ i W ~ i j \tilde D_{ii}=\sum_i \tilde W_{ij}D~ii=∑iW~ij
最终得到图卷积公式:
x ⋆ G g θ = θ ( D ~ − 1 / 2 W ~ D ~ − 1 / 2 ) x x \star_{G} g_{\theta}=\theta (\tilde D^{-1 / 2} \tilde W \tilde D^{-1 / 2})xx⋆Ggθ=θ(D~−1/2W~D~−1/2)x
上述公式中是忽略 i n p u t inputinput c h a n n e l channelchannel 和 o u t p u t outputoutput c h a n n e l channelchannel 的,若考虑的话,每个卷积核的参数是 i n p u t inputinput c h a n n e l channelchannel 数乘以 o u t p u t outputoutput c h a n n e l channelchannel 数。
GCN的特点:
在忽略i n p u t inputinput c h a n n e l channelchannel 和 o u t p u t outputoutput c h a n n e l channelchannel 的情况下,卷积核只有
1个可学习的参数,极大的减少了参数量。虽然卷积核大小减少了(GCN仅仅关注于一阶邻域,类似于3X3的经典卷积),但是作者认为通过多层堆叠GCN,仍然可以起到扩大感受野的作用。
与此同时,这样极端的参数削减也受到一些人质疑。他们认为每个卷积核如果只设置一个可学习参数,会降低模型的能力。
- 如果将传统图像的每一个像素视为 graph 的一个节点,节点之间为 八邻域链接,图像也可以看做一张特殊的图。那么在每个 3*3 的卷积核里,仅存在 1个可学习的参数 。
- 从目前应用在 image 的深度学习经验看来,这样的卷积模型复杂度虽然低 ,但是模型的能力也遭到了削弱,可能难以处理复杂的任务。
3. 空域图卷积
虽然图谱卷积有很优美得数学原理作为支撑,但也存在很多缺陷:
1️⃣ 图谱卷积不适用于有向图:
- 图傅里叶变换的应用是有限制,仅限于在无向图 。
- 谱域 图卷积的第一步是要将空信号转换到谱域,当图傅里叶变换无法使用时 , 谱域图卷积也就无法进行下去 。
- 在大量的实际场景中, W i j ≠ W j i W_{ij} \neq W_{ji}Wij=Wji
2️⃣ 图谱卷积假定 固定的图结构:
x ⋆ G g = F − 1 ( F ( x ) ⊙ F ( g ) ) = U ( U T x ⊙ U T g ) x \star_{G} g=\mathcal{F}^{-1}(\mathcal{F}(x) \odot \mathcal{F}(g))=U\left(U^{T} x \odot U^{T} g\right)x⋆Gg=F−1(F(x)⊙F(g))=U(UTx⊙UTg)
U UU 必须预先已知且固定不变- 模型训练期间,图结构不能变化(不能改变节点之间的权重,不能增删节点)。
- 图结构一旦变化,图的拉普拉斯矩阵L LL就变了,图的特征向量U UU变了,也即图傅里叶变换时基函数变了,则在卷积核上学习到的参数就无意义。
- 在某些场景下,图结构可能会变化(如社交网络数据、交通数据)。
- 模型训练期间,图结构不能变化(不能改变节点之间的权重,不能增删节点)。
3️⃣ 模型复杂度问题
SCNN需要进行拉普拉斯矩阵的谱分解,计算耗时,复杂度为 O ( N 3 ) O(N^3)O(N3)。ChebNet和GCN不需要进行谱分解,但是其可学习的参数过于简化,降低模型复杂度的同时也限制了模型的性能。
能否绕开图谱理论,重新定义图上的卷积呢?
- 空域图卷积
- 不依靠图谱卷积理论,直接在空间上定义卷积操作。
- 定义直观,灵活性更强。
- 和谱域图卷积相比,缺少数学理论支撑。
3.1 GNN
《A Generalization of Convolutional Neural Networks to Graph-Structured Data》
- GNN模型是如何定义图上的卷积?
- 回答1:卷积即固定数量的邻域节点排序后 ,与相同数量的卷积核参数相乘求和 。
- 传统卷积的有着固定的邻域大小(如 3 × 3 3\times33×3 的卷积核即为八邻域 的卷积核 ),同时有着固定的顺序(一般为左上角 到右下角)。
- 图具有 序列无序性 和 维数可变性,所以不能直接使用传统的卷积,因此,GNN 往传统的方向靠近。
- GNN 卷积思想是:固定数量邻域节点排序后,与相同数量的卷积核参数相乘求和。实际上是指,GNN认为卷积分为两步,第一步构建邻域,第二步对邻域上的节点与卷积核参数进行内积操作(相乘求和)。下图是经典卷积的例子,第一步,要对下标为1x1的节点(下标从0开始)构建邻域,根据图片的特点,很容易构建3x3大小的邻域,因为图片本身像素之间有 八邻域的内在的结构,同时这个邻域有从左上角到右下角的固有的顺序,第二步,对邻域的点进行卷积操作,具体而言就是将卷积核参数和邻域上的信号进行内积,GNN就是按这个思想展开工作(即采用固定数量的卷积核,而且卷积核是有顺序的)。

GNN 核心思想:
- 卷积的操作分为两步:
- 第一步:构建邻域。
- 找到固定数量的邻居节点 。
- 对找到的 邻居节点 进行排序 。
- 对于图结构数据而言:不存在固定八邻域结构。而且每个节点的邻域大小是变化的;同时,同一个邻域内的节点不存在顺序。
- 第二步:对邻域的点与卷积核参数进行内积。
- 第一步:构建邻域。
如何找到固定数量的邻居节点,邻居节点如何排序的?
使用随机游走的方法,根据被选中的概率期望大小选择固定数量的邻居节点。
然后根据节点被选择的概率期望来对邻域进行排序。
符号标记
- P PP 为图上的随机游走转移矩阵,其中 P i j P_{ij}Pij 表示由 i ii 节点到 j jj 节点的转移概率。
- 相似度矩阵(similarity matrix)为 S SS,可以理解为邻接矩阵。
- D DD 为度矩阵,D i i = ∑ j S i j D_{ii}=\sum_jS_{ij}Dii=∑jSij
具体步骤:
- 选择邻域:
1️⃣ GNN 假设存在图转移矩阵 P PP。假如图结构是已知的,那么 S SS 和 D DD 即为已知。因此,随机游走概率转移矩阵定义如下: P = D − 1 S P=D^{-1}SP=D−1S
使用归一化的邻接矩阵来作为转移矩阵。
根据概率转移矩阵 P PP ,可以求的 k kk 步内由 i ii 节点出发到 j jj 节点的期望访问数。
2️⃣ 随机游走概率转移矩阵 P PP 定义好了,接下来定义 多步的转移期望:
Q ( 0 ) = I , Q ( 1 ) = I + P , ⋯ , Q ( k ) = ∑ i = 0 k P k Q^{(0)}=I,\quad Q^{(1)}=I+P,\quad \cdots,\quad Q^{(k)}=\sum\limits_{i = 0}^k {{P^k}}Q(0)=I,Q(1)=I+P,⋯,Q(k)=i=0∑kPk
其中, Q i j ( k ) Q^{(k)}_{ij}Qij(k) 为 k kk 步内,由 i ii 节点出发到 j jj 节点的期望访问数。
上图是三个状态下某个节点到其他节点的期望访问数,0 步就是单位阵,只能自己到自己,1步是一个一阶转移矩阵,表示走了一步,依此类推,走 k kk 步就是 P k P^kPk(和马尔可夫模型中的概率转移矩阵是一模一样的)。
3️⃣ 根据期望大小来选择邻域
π i ( k ) ( c ) {\pi _i}^{(k)}(c)πi(k)(c) 表示节点的序号。该节点为( k kk 步内)由 i ii 节点出发的访问期望数第 c cc 大的节点。那么有: Q i π i ( k ) ( 1 ) > Q i π i ( k ) ( 2 ) > . . . > Q i π i ( k ) ( N ) {Q_{i{\pi _i}^{(k)}(1)}} > {Q_{i{\pi _i}^{(k)}(2)}} > ... > {Q_{i{\pi _i}^{(k)}(N)}}Qiπi(k)(1)>Qiπi(k)(2)>...>Qiπi(k)(N)
比如说,要选择期望最大的三个节点,那就选择期望最大的前三个,然后根据期望的大小进行排序即可,这样即选择出了想要的邻域。
- 內积操作
4️⃣ 执行 1 D 1D1D 卷积
Conv 1 ( x ) = [ x π 1 ( k ) ( 1 ) ⋯ x π 1 ( k ) ( p ) x π 2 ( k ) ( 1 ) ⋯ x π 2 ( k ) ( p ) ⋮ ⋱ ⋮ x π N ( k ) ( 1 ) ⋯ x π N ( k ) ( p ) ] ⋅ [ w 1 w 2 ⋮ w p ] \operatorname{Conv}_{1}(\mathbf{x})=\left[\begin{array}{ccc} x_{\pi_{1}^{(k)}(1)} & \cdots & x_{\pi_{1}^{(k)}}(p) \\ x_{\pi_{2}^{(k)}(1)} & \cdots & x_{\pi_{2}^{(k)}(p)} \\ \vdots & \ddots & \vdots \\ x_{\pi_{N}^{(k)}(1)} & \cdots & x_{\pi_{N}^{(k)}(p)} \end{array}\right] \cdot\left[\begin{array}{c} w_{1} \\ w_{2} \\ \vdots \\ w_{p} \end{array}\right]Conv1(x)=⎣⎢⎢⎢⎢⎡xπ1(k)(1)xπ2(k)(1)⋮xπN(k)(1)⋯⋯⋱⋯xπ1(k)(p)xπ2(k)(p)⋮xπN(k)(p)⎦⎥⎥⎥⎥⎤⋅⎣⎢⎢⎢⎡w1w2⋮wp⎦⎥⎥⎥⎤
总结:
当已知概率转移矩阵 P PP 之后,对于 i ii 节点选择期望最大的 p pp 个节点作为 i ii 节点的邻域,并且根据期望的大小对 p pp 个节点由大到小排序。
第二步为 执行1 D 1D1D卷积就,邻居节点有 p pp 个,自然卷积核的参数也有 p pp 个。
总的来说 GNN 就是使用了随机游走的方法,给每个节点选择了最紧密相联的 p pp 个节点作为邻域,然后再与固定大小的卷积核参数来进行内积。
本质上,GNN 的做法是强制将一个图结构数据变化为了一个类似规则数据。从而可以被 1 D 1D1D 卷积所处理。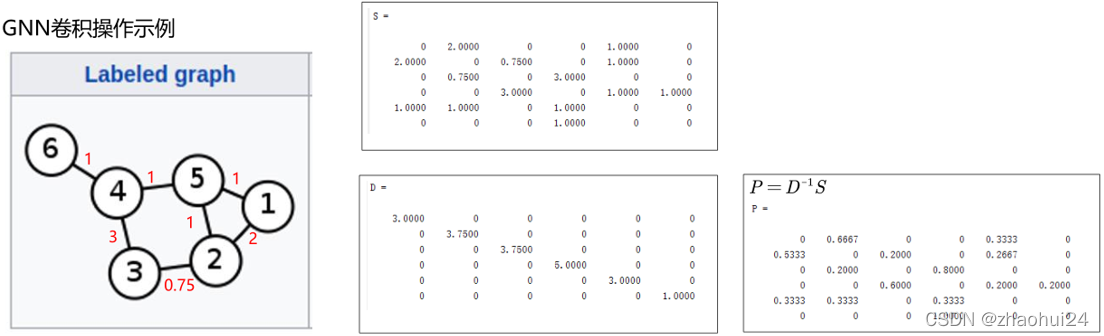
邻接矩阵 S SS ,度矩阵 D DD ,概率转移矩阵 P PP 是对邻接矩阵 S SS 做了归一化,使得每一行加起来为 1,它代表概率 P i j P_{ij}Pij 由 i ii 节点到 j jj 节点的转移概率。( P PP 不是对称矩阵)
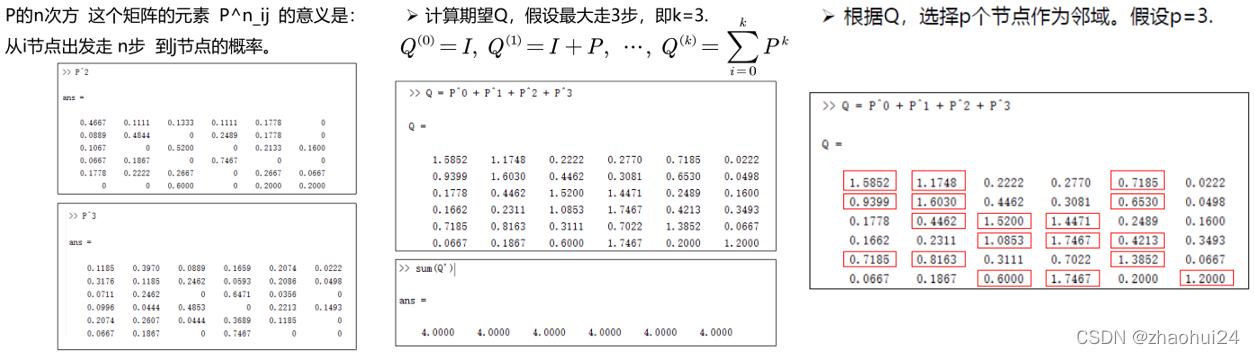
Q QQ 矩阵代表 k kk 步内 i ii 节点出发到 j jj 节点的期望访问数,也就是把前面走的步数的概率都加起来,上面是 k = 3 k=3k=3,加起来是4,因为 k kk是从 0 开始的,0 步就代表它本身。
右图中 5 号节点最终没有选择 4 号节点,而是选择了1,2号节点和它本身,这就是 P PP 矩阵的作用,找到固定大小的节点并且排序之后,接下来就可以执行 1 D 1D1D 卷积了。
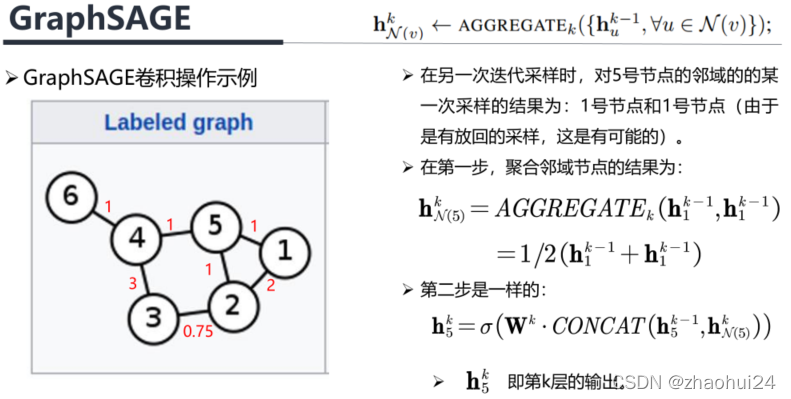
3.2 GraphSAGE
《Inductive Representation Learning on Large Graphs 》
- GraphSAGE 模型是如何定义图上的卷积?
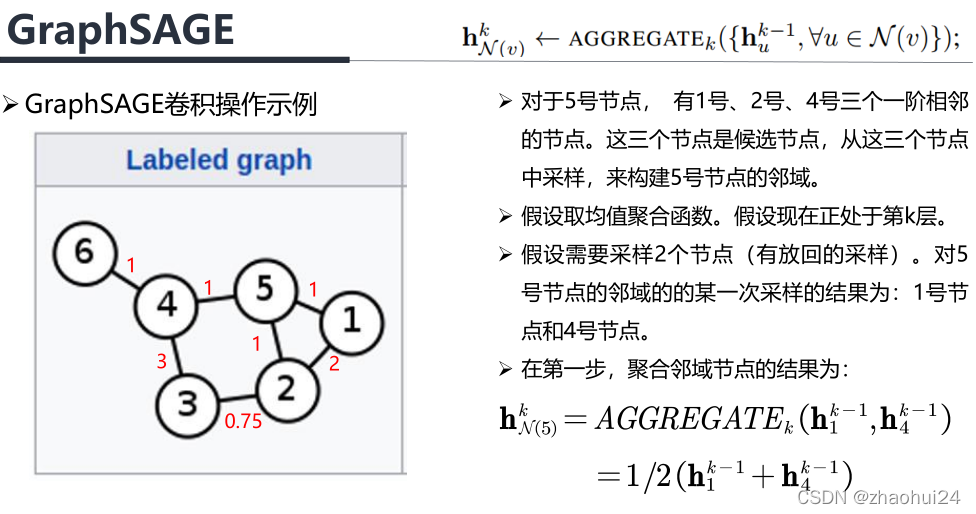
- 回答2:卷积 = 采样 + 信息的聚合
- 通过采样,得到邻域节点;
- 使用聚合函数来聚合邻居节点的信息,获得目标节点的 embedding (特征);
- 利用节点上聚合得到的信息,来预测节点 / 图的 label 。
- 回答2:卷积 = 采样 + 信息的聚合
GraphSAGE 核心思想:
- 将卷积分为采样和聚合两步
SAGE的简写为: Sample and AggreGatE
- 聚合函数必须与输入顺序无关。即作者认为邻域的节点不需要进行排序。
1️⃣采样
- GraphSAGE采用均匀采用法(Uniform Sampling)来采样固定的邻域节点。即对于某一节点,在其一阶相连的节点上均匀采样以构建一个固定节点数量的邻域。
1️⃣聚合
Mean aggregator,h v k ← σ ( W ⋅ MEAN ( { h v k − 1 } ∪ { h u k − 1 , ∀ u ∈ N ( v ) } ) \mathbf{h}_{v}^{k} \leftarrow \sigma\left(\mathbf{W} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{v}^{k-1}\right\} \cup\left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\}\right)\right.hvk←σ(W⋅MEAN({hvk−1}∪{huk−1,∀u∈N(v)})
- 均值聚合:对邻域内的节点取一个平均值,与顺序无关。如有五个数取均值,它们的顺序是与最终的均值无关的,或者说不会影响均值。
LSTM aggregator
- 使用 LSTM 来encode邻居的特征。这里忽略邻居之间的顺序,即随机打乱,输入到 LSTM 中
Pooling aggregator, AGGREGATE k p o o l = max ( { σ ( W p o o l h μ i k + b ) , ∀ u i ∈ N ( v ) } ) \text{AGGREGATE}_{k}^{pool} =\text{max}(\{ \sigma( \mathbf{W}_{pool} \mathbf{h}_{\mu_i}^{k} +b), \forall u_i \in \mathcal{N}(v)\})AGGREGATEkpool=max({σ(Wpoolhμik+b),∀ui∈N(v)})
- Pooling聚合:使用了最大值的 Pooling 聚合,与顺序无关。
GNN 采用随机游走的方法找到邻居节点之后,这些邻居节点就不再变化,而GraphSAGE 每次迭代都会进行一次采样,所以对于同样的节点,它的邻居可能是会变化的。

第一步输入 Input:图 G ( V , E ) \mathcal{G}(\mathcal{V},\mathcal{E})G(V,E) ,V \mathcal{V}V 表示节点的集合,E \mathcal{E}E表示边的集合。输入特征用 x v \mathbf{x}_vxv 表示,x v \mathbf{x}_vxv 代表 v \mathcal{v}v 节点上的特征。depth \text{depth}depth K \mathbf{K}K 代表网络的深度,也就是这个网络有 K KK 层。权重矩阵 W k \mathbf{W}^{k}Wk 代表第 k kk 层的卷积核参数,σ \sigmaσ 是非线性的函数,一般使用ReLu和sigmoid函数, AGGREGATE k \text{AGGREGATE}_{k}AGGREGATEk 是聚合函数, k kk 表示第 k kk 层,最GraphSAGE通过均匀采样来构建邻域。
第二步输出 Output: h v 0 h^0_vhv0 代表第 0 层的 v vv 节点上的信号或者特征,第 0 层就是输入信号 x v x_vxv,然后进入两个 for 循环,外面的循环是针对每一层而言的,从 k = 1... K k=1... Kk=1...K,在每层之内使用 for 循环依此遍历这层的每个节点。
看看一层内的每个节点是怎么处理的:
首先通过 AGGREGATE k \text{AGGREGATE}_{k}AGGREGATEk 函数聚合出邻域节点的信息, u uu 就是 v vv 节点的邻域,h u k − 1 h^{k-1}_uhuk−1 就是上一层的特征,是k kk 层的输入。假设通过取平均值的方式进行聚合, 即把 v vv 邻域的节点加起来取一个平均,得到邻域的信息。
然后对邻域的节点的信息在 CONCAT \text{CONCAT}CONCAT 节点本身的信息。CONCAT \text{CONCAT}CONCAT 操作就是串联,就是将两个向量首尾相接的拼起来,和经典卷积是一样的。比如在进行 3x3 的卷积操作的时候,不仅仅考虑周围的 8个节点的信息,中心节点自己也要参与计算。串联之后再经过了一个可学习的参数 W k \mathbf{W}^{k}Wk 做了一个线性变换, W k \mathbf{W}^{k}Wk 是第 k kk 层的线性变换的参数,是可学习的。实际上,这里的 W k \mathbf{W}^{k}Wk 担任了卷积核参数的角色,再通过一个激活函数得到输出。

3.3 GAT
- GAT 模型是如何定义图上的卷积?
- 回答3:卷积可定义为利用注意力机制(attention)对邻域节点有区别的聚合。
- 什么是attention?
- 注意力机制是一种能让模型对重要信息重点关注并充分学习吸收的技术。它模仿了人类观察物品的方式。核心逻辑就是「从关注全部到关注重点」
GAT 核心思想:
GAT 核心思想将 attention 引入到图卷积模型中。
作者认为邻域中所有的节点共享相同卷积核参数会限制模型的能力。因为邻域内的每一个节点和中心节点的关联度都是不同的,在卷积聚合邻域节点信息时需要对邻域中的不同的节点区别对待。
利用Attention机制来建模邻域节点与中心节点的关联度。
具体步骤:
1️⃣ 利用注意力机制计算节点之间的关联度
计算关联度:e i j = α ( W h ⃗ i , W h ⃗ j ) = a ⃗ T [ W h ⃗ i ∥ W h ⃗ j ] e_{i j}=\alpha\left(\mathbf{W} \vec{h}_{i}, \mathbf{W} \vec{h}_{j}\right)=\vec{a}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]eij=α(Whi,Whj)=aT[Whi∥Whj]

- 其中 h ⃗ i ∈ R F \vec{h}_{i} \in \mathbb{R}^Fhi∈RF 表示 i ii 节点的特征,F FF 表示节点特征的通道数。W ∈ R F × F ′ \mathcal{W} \in \mathbb{R}^{F \times F^{\prime}}W∈RF×F′ 是可学习的线性变换参数。
- α ( ⋅ ) : R F ′ × R F ′ → R \alpha(\cdot): \mathbb{R}^{F^{\prime}} \times \mathbb{R}^{F^{\prime}} \rightarrow \mathbb{R}α(⋅):RF′×RF′→R 表示注意力机制,其输出 e i j e_{i j}eij 为注意力系数。
- 在实验中 α ( ⋅ ) \alpha(\cdot)α(⋅) 的实现是一个单层前馈神经网络。∣ ∣ ||∣∣ 表示拼接,即两个向量首尾相接。α ⃗ T ∈ R 2 F ′ \vec{\alpha}^T \in \mathbb{R}^{2F^{\prime}}αT∈R2F′ 为可学习参数。
softmax归一化- 为使不同节点之间的注意力系数易于比较,作者使用
softmax函数对每个节点的注意力系数进行归一化。
α i j = softmax j ( e i j ) = exp ( e i j ) ∑ k ∈ N i exp ( e i k ) \alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)}αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)
- 为使不同节点之间的注意力系数易于比较,作者使用
2️⃣ 利用注意力系数对邻域节点进行有区别的信息聚合,完成图卷积操作。
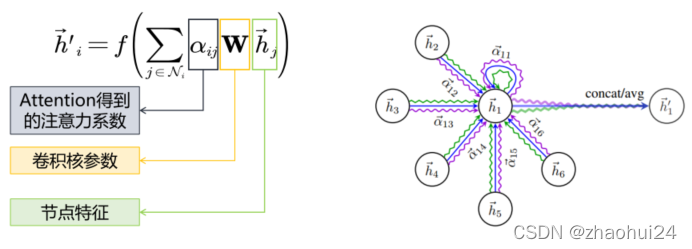
上面是图卷积操作,首先假设忽略注意力系数,即 α i j = 1 \alpha_{ij}=1αij=1,那么实际上就是对每个节点做了一个线性变换,然后再求和,GAT的卷积核参数 W \mathbf{W}W 也是所有邻域内节点共享的。当加入注意力系数后,即是在对周围的邻域节点信息进行聚合的时候,需考虑 α i j \alpha_{ij}αij, α i j \alpha_{ij}αij 比较大,意味着 j jj 节点与中心的 i ii 节点关系紧密,贡献比较大,反之则贡献就小。这就是 Attention机制 的目的,即更加关注于重要的节点,而较少关注不重要的节点(不是忽略)。
GAT 引入了 Attention机制,可以构建相邻节点的关系,是对邻域节点的有区别的聚合。若将α i j \alpha_{ij}αij 和 W \mathbf{W}W结合起来看作一个系数,实际上GAT 对邻域的每个节点隐式地分配了不同的卷积核参数。
GAT 可认为是对局部图结构的一种学习。Attention 机制可认为是一个带有可学习参数的可学习函数。利用Attention 机制,GAT 通过构建一个可学习的函数来得到相邻节点之间的关系,即局部图结构。


3.4 PGC
《Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition》
- PGC 模型是如何定义图上的卷积?
回答4:卷积可定义为是特定的采样函数(sample function)与特定的权重函数(weight function)相乘后求和。
从经典卷积出发
- K × K K \times KK×K的卷积核可以写成下式:f out ( x ) = ∑ h = 1 K ∑ w = 1 K f in ( p ( x , h , w ) ) ⋅ w ( h , w ) f_{\text {out }}(\mathbf{x})=\sum_{h=1}^K \sum_{w=1}^{K} f_{\text {in }}(\mathbf{p}(\mathbf{x}, h, w)) \cdot \mathbf{w}(h, w)fout (x)=h=1∑Kw=1∑Kfin (p(x,h,w))⋅w(h,w)
- K KK 是卷积核大小(常见为 3)。P ( ) P( )P()为一个采样函数,即在邻域内依次取出节点,来参与卷积计算。w ( ) \mathbf{w}()w()为权重函数,对取出来的节点分配卷积核参数。
- 整个式子 实际上是节点特征与卷积核参数的内积。
PGC是从经典卷积出发,来得出卷积是特定的取样函数与特定的权重函数相乘后求和。用上面的公式举例,一个 3x3 的卷积核有9个信号,当 h = 1 h=1h=1, w = 1 w=1w=1 时,则取 x 11 x_{11}x11,也就是 3x3 的左上角的节点。当 h = 3 h=3h=3, w = 3 w=3w=3 时,则取 x 33 x_{33}x33,也就是 3x3 的右下角的节点,总之随着 h hh 和 w ww 的不断地变化(1-3,1-3),就可以取到 3x3 邻域上的 9 个不同的节点,权重函数 w ( ) \mathbf{w}()w() 也是一样的,每取到一个节点的时候,对该节点分配一个卷积核的参数,这样 3x3 的邻域内就是 9 个节点上的信号和 9 个卷积核参数的内积。以上是在经典卷积中对于取样函数和权重函数的定义。
PGC 核心思想:
将卷积从规则数据扩展到图结构数据的过程中,选择合适的取样函数和权重函数。
f out ( x ) = ∑ h = 1 K ∑ w = 1 K f in ( p ( x , h , w ) ) ⋅ w ( h , w ) f_{\text {out }}(\mathbf{x})=\sum_{h=1}^{K} \sum_{w=1}^{K} f_{\text {in }}(\mathbf{p}(\mathbf{x}, h, w)) \cdot \mathbf{w}(h, w)fout (x)=h=1∑Kw=1∑Kfin (p(x,h,w))⋅w(h,w)
取样函数
- 取样函数在邻域内依次取出节点。重点在于如何构建节点的邻域,也即取样函数在哪取样。
- 在图结构数据上,PGC 可以定义取样函数在 D 阶近邻的节点上。即 B ( v i ) = { v j ∣ d ( v j , v i ) ≤ D } B(v_i)=\{v_j|d(v_j,v_i)\leq D\}B(vi)={vj∣d(vj,vi)≤D},其中d ( v j , v i ) d(v_j,v_i)d(vj,vi) 表示从i ii 节点到 j jj节点的最短距离。B ( v i ) B(v_i)B(vi) 代表 i ii 节点的邻域,即 若 j jj 节点和 i ii 节点的距离小于等于 D DD,则 j jj 就是 i ii 的邻域节点。
- 在实验中取D = 1 D=1D=1,且在 1 阶邻域中挨个取样。但也可以设置为其它的邻域。
权重函数
- 首先将邻域内的点分为K KK 个不同的类
- l i l_ili: B ( v i ) → { 0 , . . . , K − 1 } B(v_i) \rightarrow \{0,..., K-1\}B(vi)→{0,...,K−1}
- l i ( ⋅ ) l_i(\cdot)li(⋅) 表示 i ii 节点的分类映射。B ( v i ) B(v_i)B(vi)表示 i ii 节点的邻域节点。{ 0 , ⋯ , K − 1 } \{0,\cdots, K-1\}{0,⋯,K−1} 为分类类别。
- 由于分类操作,因此本方法称之为Partition Graph Convolution (PGC)。
- 每一类共享一个卷积核参数。不同类之间卷积核参数不同。w ( v i , v j ) = w ′ ( l i ( v j ) ) \mathbf{w}(v_i, v_j)= \mathbf{w}^{\prime}(l_i(v_j))w(vi,vj)=w′(li(vj))
权重函数这样设计是有很强的泛化性的,比如划分成 K = 1 K=1K=1,也就是划分成 1 类,则这样,就是所有的节点共享一个卷积核参数。现在假如邻域大小等于类别数,意思就是说每一个节点划分到一个类中去,每个节点享用的卷积核参数都不一样,这就有点类似与 GNN 的方法。而介于这两者中间,则成为一种中间态。
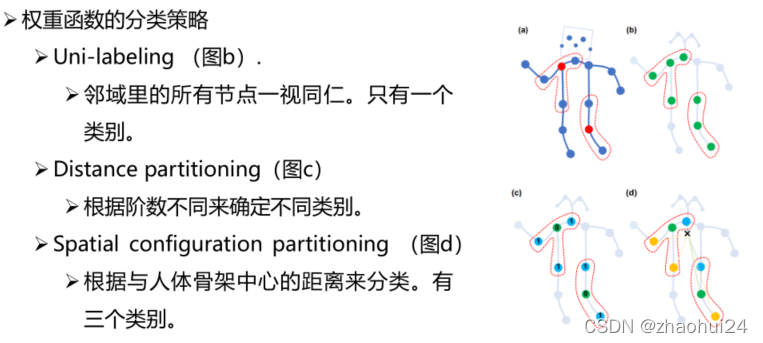
(图d)“x” 代表人体骨架中心,若 “x” 到邻域节点的距离小于到中心节点的距离,则划成一类(蓝色),若大于,则划分成另一类(黄色),等于当然也划成一类(绿色)。
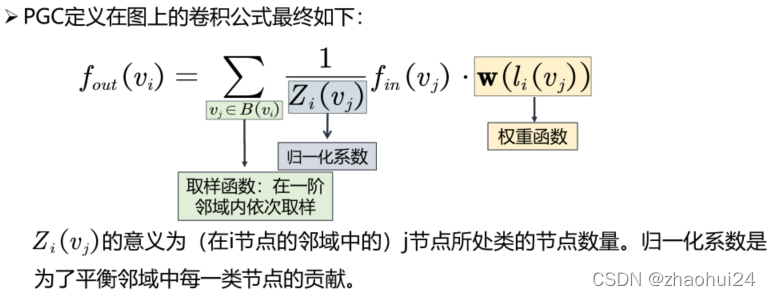
首先是取样函数(在一阶邻域内依次取样,取到了 j jj 节点);接着 f i n ( v j ) f_{in}(v_j)fin(vj) 就表示将 j jj 节点转换成它的特征;之后分配权重,给 j jj 节点分类, l i ( ⋅ ) l_i(\cdot)li(⋅) 函数表示分类,根据不同的类别给 j jj 节点分配一个不同的权重函数,实际上是特征与卷积核参数的内积;最后使用一个归一化系数。

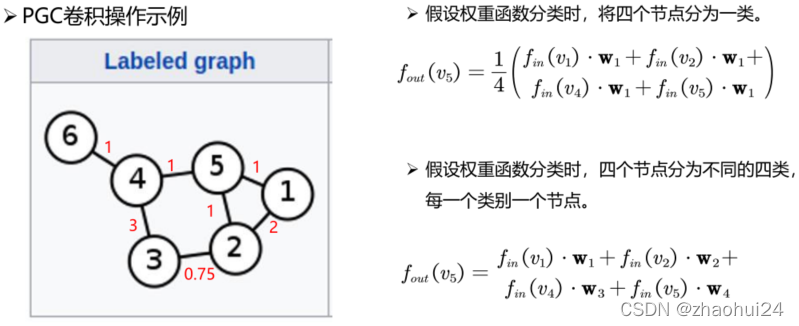
| GNN | GraphSAGE | GAT | PGC | |
|---|---|---|---|---|
| 邻域节点选择方法 | 通过随机游走的概率大小来构建邻域 | 通过均匀采样构建邻域 | 直接选用一阶相邻节点作为邻域节点 | 由特定的取样函数决定 |
| 邻域节点是否需要排序 | 需确定邻域节点的顺序 | 邻域节点不需要确定顺序 | 无需排序 | 由特定的权重函数决定 |
| 同一邻域内,卷积核参数是否共享 | 邻域里的每个节点拥有不同的卷积核参数 | 邻域里所有节点共享同样的卷积核参数 | 共享卷积核参数 | 由特定的权重函数决定 |
1. 参考链接 - 深蓝学院 - 图卷积神经网络
2. 参考链接 - Ma Sizhou - 图卷积神经网络笔记
3. 参考链接 - 三景页三景页 - 可变形卷积从概念到实现过程
4. 参考链接 - bujiatang - GNN学习笔记