最近点对问题
什么是最近点对问题
算法第二次实验是求解最近点对问题 同时对算法进行分析,这里仅对解决二维最近点对问题做探讨
首先就是最近点对问题的引入
最近点对是指在平面/直线上分布许多点,同时这些点不重复,其中最近的一对点就是最近点对。
二维情况下的问题
如果一维情况下的点如果取一中心线分隔开求解左右最小的d那么左右至多只能存在一个点
但二维则不同,在左右最小d求出来后仍然可能存在许多点 又该如何求解呢?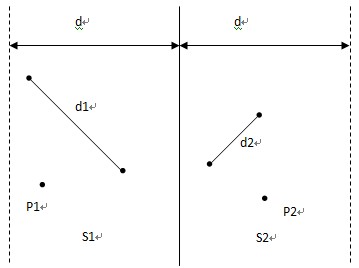
代码基本框架
首先是预定义点的类或者结构体用以存放数据,Double类型的数据变量存放x,y.
class Point
{
double x,y;
public:
Point(){x=0;y=0;}
Point(double a,double b)
{x=a;y=b; //构造函数 }
double GetPoint_X()
{return x; //返回点的x坐标 }
double GetPoint_Y()
{return y; //返回点的y坐标 }
~Point(){}
void SetPoint(double a,double b)
{x=a;y=b; //设置点坐标 }
};
void CopyPoint(Point A[],Point B[],int m,int n)
{
for(int i=0;m<=n;i++,m++)
A[i].SetPoint(B[m].GetPoint_X(),B[m].GetPoint_Y());
}
double ForceMethod(Point arr[],int Num)
{
//蛮力法
}
double Merge(Point arr[],double Mindis1,int Num)
{
//递归调用的合并函数
}
double Dichotomy(Point arr[],int Low,int High)
{
//递归的分解函数
}
int main()
{
//main 函数
}
蛮力法及其代码
对于这类问题,最容易想到的解法就是蛮力法直接暴力查解,代码实现简单易懂。
整体思路对于每一个点都和其他的N-1个点都进行一次比较,记录最小距离的点对即可。
double ForceMethod(Point arr[],int Num)
{
//蛮力求解算法
double Mindis=999999; //存放最小距离
double Minx[2],Miny[2]; //存放最小距离两个点坐标
for(int i=0;i<Num;i++)
for(int j=i+1;j<Num;j++)
{
double dis=GetDis(arr[i],arr[j]);
if(Mindis>dis)
{
Mindis=dis;
Minx[0]=arr[i].GetPoint_X();
Minx[1]=arr[j].GetPoint_X();
Miny[0]=arr[i].GetPoint_Y();
Miny[1]=arr[j].GetPoint_Y();
}
}
cout<<"最近点对为:"<<"("<<Minx[0]<<","<<Miny[0]<<")与("<<Minx[1]<<","<<Miny[1] <<")"<<endl;
cout<<"它们的距离为:"<< Mindis<<endl;
cout<<endl;
return Mindis;
}
分治法及其代码
分治法相比于蛮力法就复杂许多了,首先需要思考何为分治?
其实算法的整体思路比较像合并排序算法
分为两个部分:
1.分解为左右子问题
对于分解 重点在于从哪分解,分到什么情况结束
首先是从哪分解?
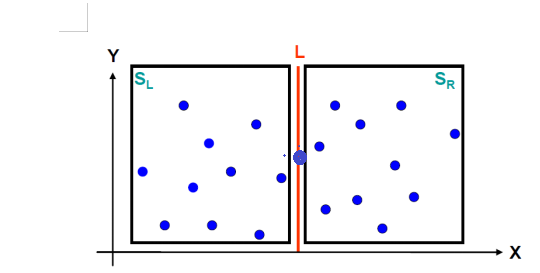
为了使得左右部分的点数目尽量均匀,我们首先需要对所有的点按x的大小进行一次排序
这样我们选取的Mid点就可以作为左右的分隔线
注:这里我选择的Mid当点数为偶数时中间有两个点选择前面那
这样得到的图应该是有一个中点在分隔线上 如下图所示
在计算的时候不要忘记把这个点放到左边的点对内进行计算。
分解到什么时候结束呢?
当只有两个点 或者三个点 时已经可以直接求出最小点对的距离了
此时自然就可以结束分解了,得出分解到最小时候的左/右的最近点对距离
这里首先给出分解与递归的代码:
Merge为合并函数 在下面来讲
//需要新建左右部分的点数组实现左右分别递归
double Dichotomy(Point arr[],int Low,int High)
{
int Num=High-Low; //Num=点数
if(Num==1)
return 9999999; //一个点时不用求了相当于无穷大
if(Num==2) //只有两个点
return GetDis(arr[0],arr[1]);
if(Num==3) //三个点
return min(GetDis(arr[0],arr[1]),min(GetDis(arr[0],arr[2]),GetDis(arr[1],arr[2])));
//其他情况
int Mid=Num%2==0?Num/2-1:Num/2;
Point *Ltemp=new Point[Mid+1];
Point *Rtemp=new Point[High-Mid-1];
CopyPoint(Ltemp,arr,Low,Mid);
CopyPoint(Rtemp,arr,Mid+1,High-1);
double dis1=Dichotomy(Ltemp,0,Mid+1); //递归调用求左
double dis2=Dichotomy(Rtemp,0,High-Mid-1); //求右
double Mindis1=min(dis1,dis2); //非跨越最小
return Merge(arr,Mindis1,Num);
}
2.合并左右子问题
合并左右是代码最关键的一个部分,因为我们需要去计算跨越中线的最小Dis
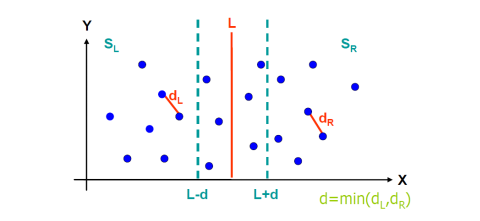
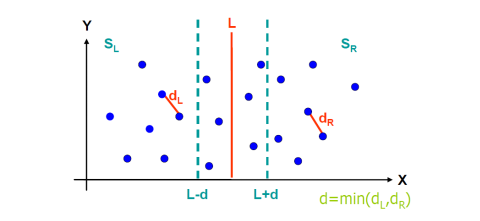
首先我们需要排除一些不可能的点来减少运算量
1.首先排除X方向上不可能的点
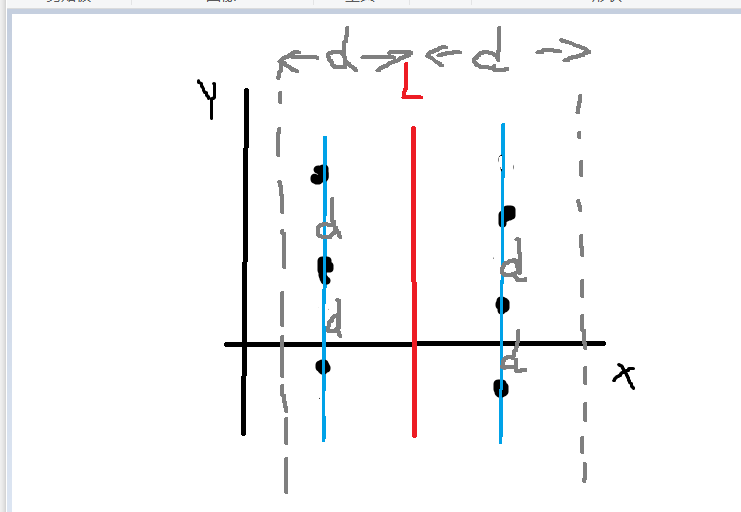
举个栗子 如下图所示
已知dl与dr是左右的最小距离
那么d=min(dl,dr).
此时我们以L为中线 L-d,L+d 为边界 可以得到一个范围
超过这个X范围的点 都不可能是最小跨越距离------因为它不可能小于d了。
这样在合并的时候就可以剔除左右超过X范围的点了,
2.求解跨越最小
然后我们分别比对范围内左边与右边的每一个点 就可以找到跨越的最小距离d2
如果d2<d了.
那么最小距离就是d2了~ 大功告成!
这里给出常规合并代码 如下
double Merge(Point arr[],double Mindis1,int Num)
{
/*
注:该部分为分治算法合并部分
合并左右 计算跨越左右的最小值 与传入的Mindis1 做比较
变量含义:
1.Mindis1:非跨越的最小点对距离 .
2.Num:左右整体的数组长度也就是待合并点个数 .
3.Mid:中间的点 靠左.
4.leftnum, rightnum: 左右符合 Mid+-Mindis1范围内的点的数量.
5.Leftarr[], Rightarr[] 左右数组 ,存放符合范围内的点的值.
*/
int Mid=Num%2==0?Num/2-1:Num/2;
int leftnum=0,rightnum=0; //记录点数量
for(int i=0;i<=Mid;i++)
{
//计算left点的数量
double len;
len=arr[i].GetPoint_X()-arr[Mid].GetPoint_X();
if(len<=0&&len> -Mindis1)
leftnum++;
}
for(int i=Mid+1;i<Num;i++)
{
//计算Right点的数量
double len;
len=arr[i].GetPoint_X()-arr[Mid].GetPoint_X();
if(len>=0&&len<Mindis1)
rightnum++;
}
//新建左右arr对象数组 并赋值
Point *Leftarr=new Point[leftnum];
Point *Rightarr=new Point[rightnum];
int Lflag=0,Rflag=0;
for(int i=0;i<=Mid;i++)
{
double len;
len=arr[i].GetPoint_X()-arr[Mid].GetPoint_X();
if(len<=0&&len> -Mindis1)
Leftarr[Lflag++].SetPoint(arr[i].GetPoint_X(),arr[i].GetPoint_Y());
}
for(int i=Mid+1;i<Num;i++)
{
double len;
len=arr[i].GetPoint_X()-arr[Mid].GetPoint_X();
if(len>=0&&len<Mindis1)
Rightarr[Rflag++].SetPoint(arr[i].GetPoint_X(),arr[i].GetPoint_Y());
}
//常规解法
double Mindis2=Mindis1;
for(int i=0;i<leftnum;i++)
for(int j=0;j<rightnum;j++)
{
double Dis=GetDis(Leftarr[i],Rightarr[j]);
if(Dis< Mindis2)
Mindis2=Dis;
}
return Mindis2;
一般分治法遇到的特殊情况
我们把重点放在如何画X范围 求解Mindis2就会发现问题
仔细观察这张图和这一小段代码
//常规解法
double Mindis2=Mindis1;
for(int i=0;i<leftnum;i++)
for(int j=0;j<rightnum;j++)
{
double Dis=GetDis(Leftarr[i],Rightarr[j]);
if(Dis< Mindis2)
Mindis2=Dis;
}
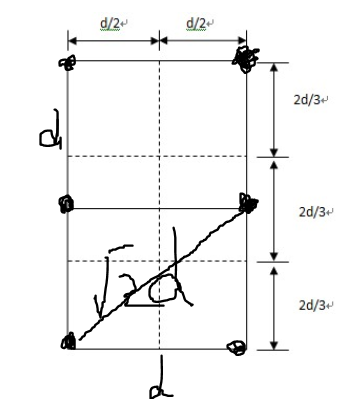
很明显 存在一种特殊情况:当左右两侧的点是这样分布的时候 (自己瞎画的 灵魂画手哈哈哈)
当左右的点都在一条直线上时,并不能通过X范围来有效的排除点
而最终求解Dis2是双重for循环嵌套的
这样的情况下该算法其实还是一种N^2的求解办法
如何优化分治法(6点确定与4点确定解法)
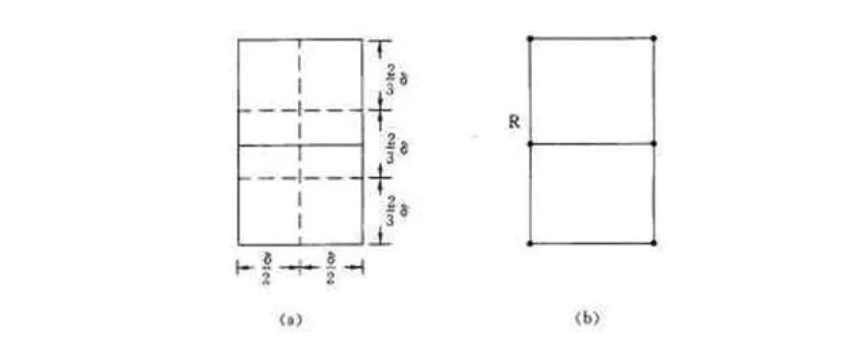
1.当一个左点确定时,右边相应的最多只用算6个点。
当某左点确定时,我们可以首先得出一个模糊的范围
这个范围大小很明显是一个矩形(从某左点往右划d的范围,再往上下各画一个d的矩形)
如下图b所示
在这样一个范围内最多有多少个点呢?我们通过一个限制条件d先来考虑一下
d的含义是左右的最短点对距离:也就是说不存在非跨越的比这个还短的点对距离
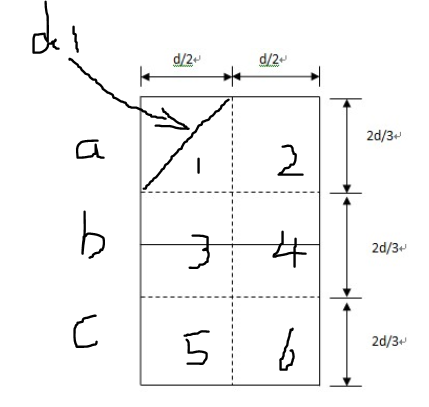
我们把这个图分为6块 如下图所示
很明显的最多的情况应该是每一块至多有一个点
这样才满足不大于d的条件
如果有7个点那么必然在某一块中会出现两个点
而某一块中最长的斜边d1只有5/6d那么长(勾股定理,如上上图第1块所示)
所以范围内必然不能存在6个以上的点,我们只需要找到范围上界或者下界运算6个点(如果有6个的话)就可以得出结果了。
这就是6点确定的由来
2.再优化,其实最多只用算4个
接下来简单说一下4点确定,其实我也没太搞懂极限情况的极值由来
这一部分是根据论文:求平面点集最近点对的一个改进算法-1998年 周玉林 熊鹏荣 朱洪
具体论文内容可以百度查阅 这里仅仅放出部分
这里可以看出 若范围2中存在点 它就要比pq点对的距离要小,所以只需要验证上/下方向上的两个点就可以得出最小的点了.若2有点 那就是比对2,3分别与p的距离。若2无点那就是比对1,3分别与p的距离。
综合成一句话就是比对Y坐标最近的四个点(如果存在4个点),如图7所示
对上面两个点和下面两个点比较就可以得出结果。
所以我们首先就要考虑对右边点按Y升序排列,然后找到这四个点分别比较。
优化后分治法(4点确定代码)
该部分替换原先常规算法那部分
//优化算法 只用考虑四个点计算
//思路参考论文:求平面点集最近点对的一个改进算法-1998年 周玉林 熊鹏荣 朱洪
sort(Rightarr,Rightarr+rightnum,Cmp_Y);
double Mindis2=Mindis1;
for(int i=0;i<leftnum;i++)
{
int temp=0; //标记点
for(int j=0;j<rightnum;j++)
{
if(Leftarr[i].GetPoint_Y()>=Rightarr[j].GetPoint_Y())
temp++;
}
//cout<<"temp:"<<temp<<endl;
//只考虑上下各两个 temp+1,temp, temp-1,temp-2;
for(int k=0;k<2&&temp+k<rightnum;k++)
{
if(GetDis(Leftarr[i],Rightarr[k+temp])<=Mindis2)
Mindis2=GetDis(Leftarr[i],Rightarr[k+temp]);
}
for(int l=1;l<=2&&temp-l>=0;l++)
{
if(GetDis(Leftarr[i],Rightarr[temp-l])<=Mindis2)
Mindis2=GetDis(Leftarr[i],Rightarr[temp-l]);
}
}
return Mindis2;
结束线------------------------------------------------------