同学们都知道,“人均消费支出”与“食品支出”二者必然存在相关性。那么,在这两个变量之间,能不能构建出一个回归方程?如果利用SPSS进行回归分析,应该选择线性回归分析,还是曲线回归分析呢?
为了回答上述问题,本文尝试以长沙市城市居民人均消费支出对食品支出的影响分析为例,详解SPSS中曲线估计的实际应用。
1 基础数据
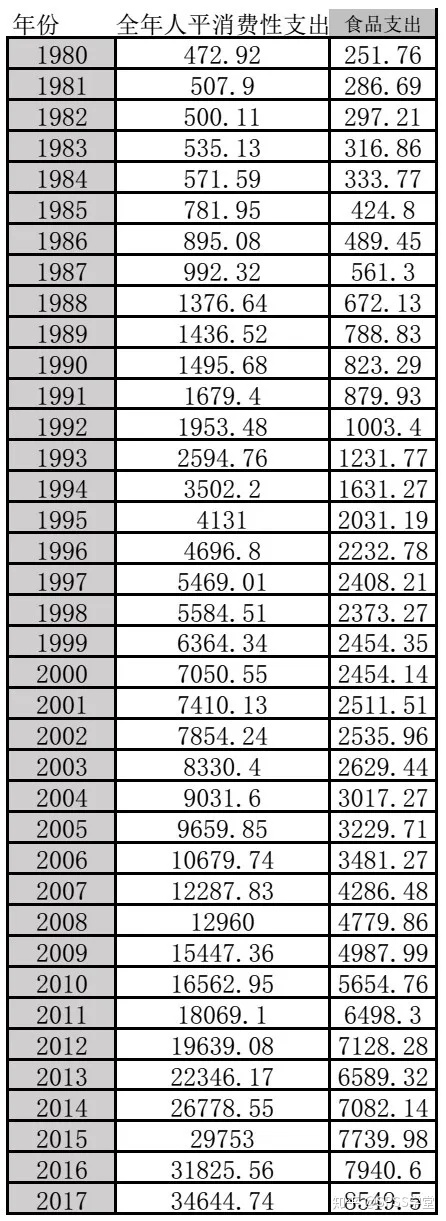
根据统计年鉴,可得到长沙市1980年-2017年城市居民调查户消费性支出情况,数据如下。
2 SPSS曲线估计操作步骤
首先,绘制散点图。观察变量之间的统计关系,根据回归线形状的直观认知,确定一个能够反映和拟合这种认知的数学函数。
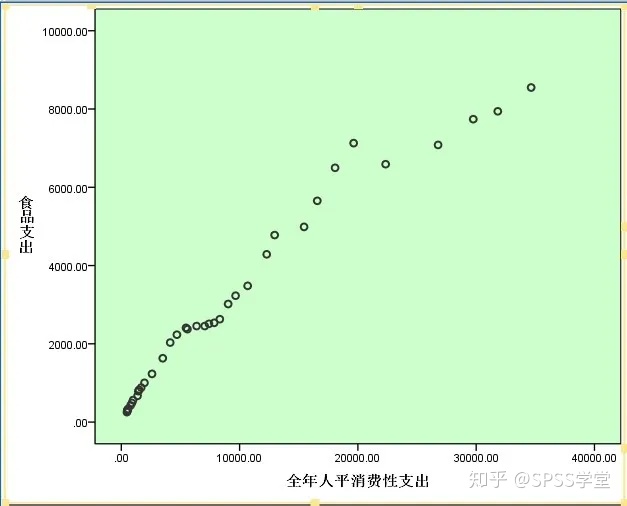
从上图可看出,二者之间可构建线性或二次曲线模型。究竟哪种模型更适合呢?
接下来,我们进行回归分析并作对比。
第1步:选择菜单:【分析(A)】→【回归(R)】→【曲线估计(C)】。
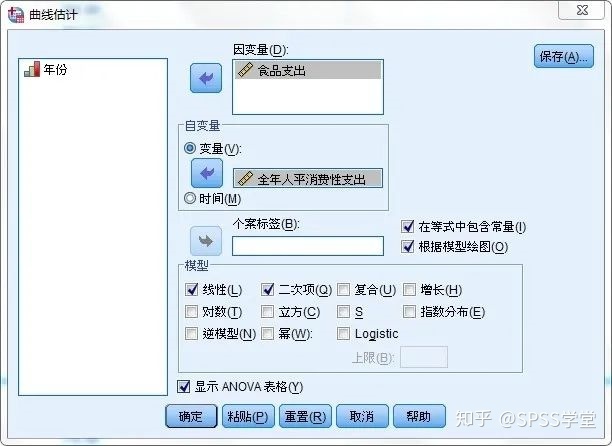
第2步:选择“食品支出”至【因变量】,“人均消费支出”至【自变量】。
第3步:在【模型】中选择“线性”“二次项”。
第4步:选择【根据模型绘图(O)】选项,绘制回归线;选择【显示ANOVA表格(Y)】,输出各个模型的方差分析和各回归系数的显著性检验结果。
3 结果分析
从输出查看器窗口可看到以下结果:
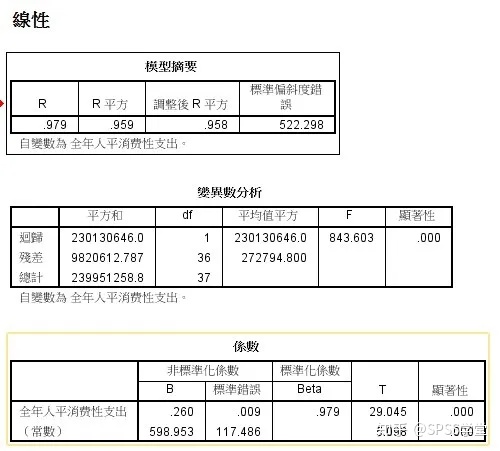
由上表可知,以食品支出为解释变量的一元线性回归方程,拟合优度判定系数为0.959,概率P-值近似于0,小于显著性水平0.05。
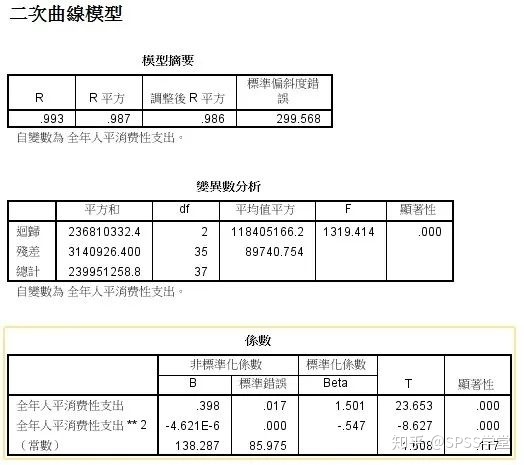
由上表可知,以食品支出为解释变量的二次曲性回归方程,拟合优度判定系数为0.987(比一元线性拟合优度0.959更好)。回归方程和各回归系数概率P-值近似于0,小于显著性水平0.05,表明二次曲线模型更具有合理性。
此外,得到回归线对比图如下:
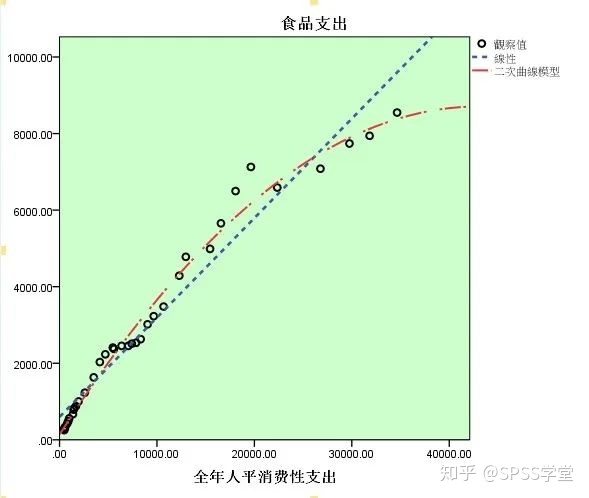
图中,红色线为二次曲线估计回归线,蓝色线为线性回归线。由此图也可看出,二次曲性比一元线性拟合优度更好。
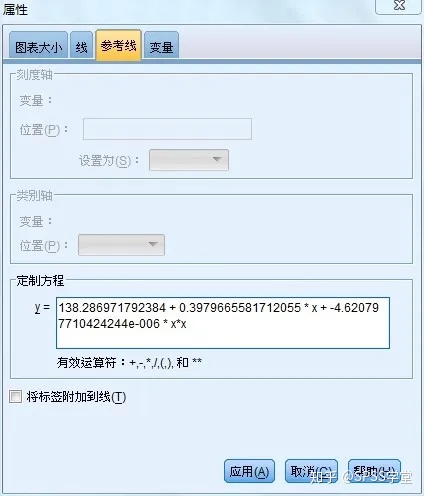
对了,想知道最终的一元二次曲线回归方程吗?SPSS也给我们写好了呢!在输出结果中,双击回归线图片,选中想要查看编辑的那条参考线,就可以在属性对话框里看到回归方程了!