算法学习

遗传算法（Genetic Algorithm,GA）

• 20世纪六七十年代由美国密歇根大学的 Holland教授创立
• 借鉴了生物的进化的自然规律：种群繁殖、基因突变、优胜劣汰、适者生存。
• 两大规律分散规律和自由组合规律

基本特征

• 智能式搜索；
• 渐进式优化；
• 全局最优解；
• 黑箱式结构；
• 通用性强（不要求明确的数学表达式）；
• 并行式运算（搜索速度快）。

基本过程

文字描述：

1. 编码、随机产生初始群体；
2. 个体评价、选择，确定是否输出；
3. 随机交叉运算；
4. 随机变异运算；
5. 转向个体评价，开始新循环。

流程图：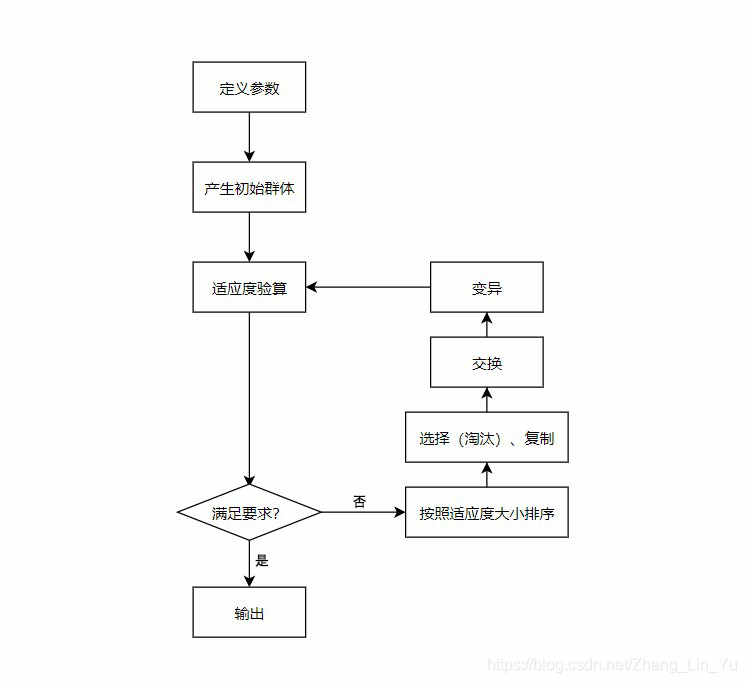

基本算子

• 复制算子
  可用轮盘方式选取复制对象，即用适应度对应扇区大小，然后随机进行对象选取。（类似于轮盘抽奖游戏）
• 交换算子
  执行交换的个体是随机的，一般交换的概率在50%~80%之间。
• 变异算子
  执行变异的个体也是随机的，一般变异概率在10%左右。
• 选择算子
  用适应度来确定是否淘汰或留下。
• 重排序算子
• 倒序算子
• 生态算子
• 显性算子

附：生态算子和显性算子用得比较少。

终止条件

1. 设定固定的繁殖代数。
2. 当有最优目标值时，可采用控制偏差的方式。
3. 检查适应度的变化。

编码原则

• 有意义积木块编码（高效）
• 最小字符积编码（简单）

粒子群算法（Particle Swarm Optimization,PSO）

• 最早由Eberhart和Kennedy于1995年提出。
• 借鉴了鸟兽捕食的群体行为。

基本特征

与遗传算法相比较

相同点：

• 种群随机初始化；
• 适应度值与目标最优解之间的映射；

不同点：

• PSO算法没有选择、交叉、变异等操作算子；
• PSO算法有记忆的功能；
• 信息共享机制不同，所以一般情况下，PSO的收敛速度更快；

基本过程

文字描述

1. 首先在可行解空间中初始化一群粒子， 每个粒子都代表极值优化问题的一个潜在最优解，每个粒子具有三项指标特征：位置、速度、适应度。
2. 粒子在解空间中运动，通过追踪个体极值Pbest和群体极值Gbest更新个体位置。（Pbest是个体所经历位置中计算得的适应度最优位置，Gbest是种群中所有粒子搜索到的适应度最优位置）
3. 粒子每更新一次位置，就计算一次适应度值，并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新Pbest和Gbest的位置。

流程图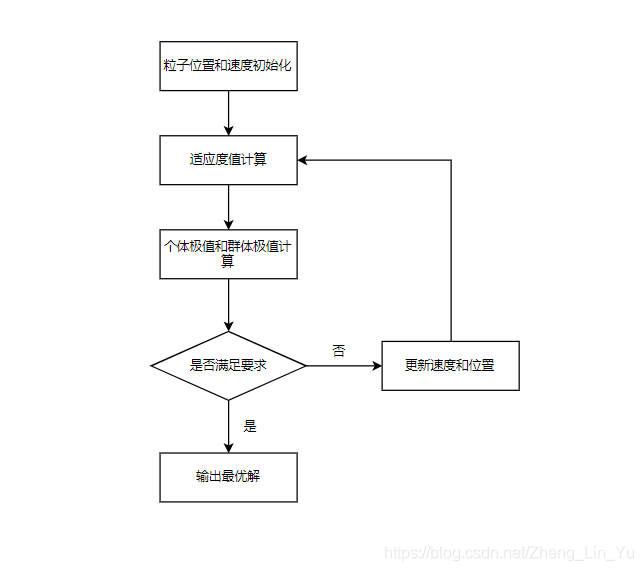

速度和位置的更新公式

终止条件

1. 设定固定的迭代代数。
2. 当有最优目标值时，可采用控制偏差的方式。
3. 检查适应度的变化。

蚁群算法（Ant Colony Algorithm,ACA）

• 由Marco Dorigo于1992年在他的博士论文中提出。
• 借鉴了蚂蚁在寻找食物过程中发现路径的行为。
• 蚂蚁在寻找食物源时，会在其经过的路径上释放一种信息素，并能够感知其他蚂蚁释放的信息素。信息素的浓度的大小表征路径的远近，信息素浓度越高，表示对应的路径距离越短。
• 路径上的信息素浓度会随着时间的推进而逐渐衰减。

基本特征

• 正反馈机制。
• 个体间通过环境进行间接地通讯。
• 分布式搜索，并行式计算。
• 启发式的概率搜索方式，不容易陷入局部最优。

基本过程

文字描述

1. 初始化各项参数，如蚁群规模m、信息素重要程度因子α、启发函数重要程度因子β、信息素挥发因子ρ、信息素释放总量Q、最大迭代次数iter_max、迭代初值iter=1。
2. 将各个蚂蚁随机地放置在不同的出发点，对每个蚂蚁计算其下一个待访问的城市，直到所有蚂蚁访问完所有的城市。
3. 计算各个蚂蚁经过的路径长度，记录当前代数中的最优解（最短路径）。同时，对各个城市连接路径上的信息素浓度进行更新。
4. 判断是否终止。如果未达到最大迭代次数，则继续进入下一代，反之，输出最优解。

流程图

相关计算公式

城市行进概率公式

信息素浓度更新公式（ant cycle system）

参数

• d：两座城市之间的距离；
• η：启发函数；
• m：蚁群规模；
• α：信息素重要程度因子，理想范围 [0, 5]；
• β：启发函数重要程度因子，理想范围 [0, 5]；
• ρ：信息素挥发因子，理想范围 [0.1, 0.99]；
• Q：信息素释放总量，理想范围 [10, 10000]；
• τ：信息素浓度；

终止条件

1. 设定固定的迭代次数。（√）
2. 当有最优目标值时，可采用控制偏差的方式。
3. 检查适应度的变化。

模拟退火算法（Simulated Annealing,SA）

• 最早的思想是由N. Metropolis等人于1953年提出。
• 借鉴了物理中固体物质的退火过程：加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

基本特征

• 和GA、PSO、ACA不同，不属于群体算法；
• 收敛速度慢，且温度管理、退火速度等对寻优结果都有影响；
• 具有概率突变特性，且能一定概率地接受非最优解，故在局部最优解时能概率性地跳出并最终趋于全局最优。

基本过程

文字描述

1. 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L ；
2. 对k=1, …, L做第3至第6步；
3. 对当前S’随机扰动产生一个新解S′ ；
4. 计算增量ΔT=C(S′)-C(S)，其中C(S)为评价函数 ；
5. 若ΔT<0则接受S′作为新的当前解S，否则以概率exp(-ΔT/T)接受S′作为新的当前解S（Metropolis准则）’
6. 如果满足终止条件则输出当前解作为最优解，结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法或者达到设定的终止温度；
7. T逐渐减小，然后转第2步。

流程图

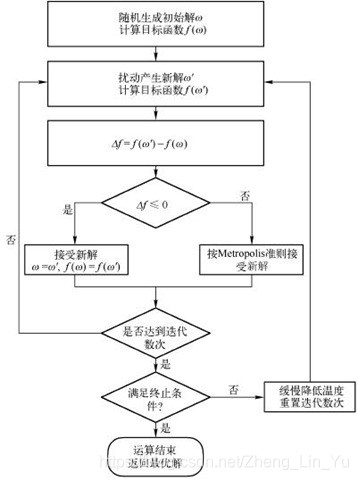
终止条件

• T降低至最低温度T_min

禁忌算法（Tabu Search）

• 禁忌搜索由美国科罗拉多大学系统科学家Glover教授于1986年在一篇论文中首次提出。
• 在对爬山法的分析基础上，做出做出三点改进①接受非最优解②引入禁忌表③引入长期记忆表和中期记忆表。
• 邻域选优的规则模拟了人类的记忆功能；

基本特征

• 全局最优解；
• 通过禁忌表避免重复搜索；
• 能够接受非最优解从而避免陷入局部最优解；

基本过程

关键词：评价函数、禁忌表（禁忌长度、禁忌步长）、领域移动、候选集、特赦规则、终止条件。

流程图

特赦规则

通俗定义：对于在禁忌的对象，如果出现以下情况，不论现在对象的禁忌长度如何，均设为0。

• 基于评价值的规则，若出现一个解的目标值好于前面任何一个最佳候选解，可特赦；
• 基于最小错误的规则，若所有对象都被禁忌，特赦一个评价值最小的解；
• 基于影响力的规则，可以特赦对目标值影响大的对象。

终止条件

• 确定步数终止原则，但无法保证解的效果，应记录当前最优解；
• 频率控制原则，当某一个解、目标值或元素序列的频率超过一个给定值时，终止计算；
• 目标控制原则，如果在一个给定步数内，当前最优值没有变化，可终止计算。