机器翻译seq2seq+Attention（理论+代码）

导语：看本文之前，你应该熟悉RNN（LSTM、GRU）工作原理、pytorch中LSTM的使用以及一些张量操作。

1.前言

seq2seq 是一个Encoder–Decoder 结构的网络，它的输入是一个序列，输出也是一个序列， Encoder 中将一个可变长度的信号序列变为固定长度的向量表达，Decoder 将这个固定长度的向量变成可变长度的目标的信号序列。如下是 Seq2Seq 模型工作的流程：

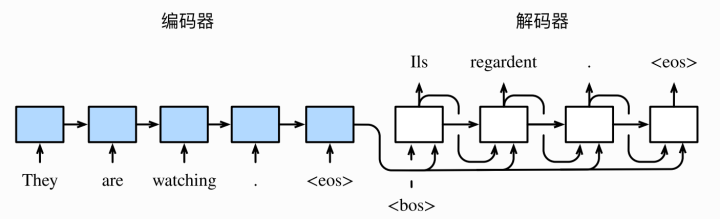
图1 一个机器翻译的案例

图1中无论是编码器还是解码器，都是用的循环神经网络，编码器用来分析输入序列，解码器用来生成输出序列。我们可以看到在编码器最后一个位置的输入是""(end of sequence)来表示序列的终止，编码器中每个时间步的输入依次为英语句子中的单词、标点和特殊符号""。在图1中使用了最终的时间步的隐藏状态作为输⼊句⼦的表征或编码信息。解码器在各个时间步中使⽤输⼊句⼦的编码信息和上个时间步的输出以及隐藏状态作为输⼊。我们希望解码器在各个时间步能正确依次输出翻译后的法语单词、标点和特殊符号""。需要注意的是，解码器在最初时间步的输⼊⽤到了⼀个表示序列开始的特殊符号""(beginning of sequence)。

2.编码器

这里的编码器是把一个不定长的序列变成了一个定长的背景变量 $c$ ，那么该背景变量就包含了输入序列的信息。常用的编码器就是循环神经网络。

假设输⼊ $x_{1}$ ，······， $x_{T}$ ，其中 $x_{i}$ 是句子中第 $i$ 个词，在时间步 $t$ ，循环神经网络将输入 $x_{t}$ 的特征向量 $\boldsymbol{x}_{t}$ 和上个时间步的隐藏状态 $h_{t-1}$ 变换为当前时间步的隐藏状态 $h_{t}$ ，在这里使用函数 $f$ 表达循环神经网络隐藏层的变换：
$\boldsymbol{h}_{t}=f\left(\boldsymbol{x}_{t}, \boldsymbol{h}_{t-1}\right)$
下面我们定义函数 $q$ 将各个时间步的隐藏状态变换为背景变量：
$\boldsymbol{c}=q\left(\boldsymbol{h}_{1}, \ldots, \boldsymbol{h}_{T}\right)$
例如，当选择 $q\left(\boldsymbol{h}_{1},\ldots,\boldsymbol{h}_{T}\right)=\boldsymbol{h}_{T}$ 时，背景变量是输⼊序列最终时间步的隐藏状态 ${h}_{T}$ 。

以上描述的编码器是⼀个单向的循环神经⽹络，每个时间步的隐藏状态只取决于该时间步及之前的输⼊⼦序列。我们也可以使⽤双向循环神经⽹络构造编码器。在这种情况下，编码器每个时间步的隐藏状态同时取决于该时间步之前和之后的⼦序列（包括当前时间步的输⼊），并编码了整个序列的信息。

3.解码器

我们已经知道编码器输出的背景变量 $c$ ，编码了整个输⼊序列 $x_{1}$ ，······， $x_{T}$ 的信息。给定训练样本中的输出序列 $y_{1}, y_{2}, \ldots, y_{T^{\prime}}$ ，对每个时间步 $t^{\prime}$ (符号与输⼊序列或编码器的时间步 $t$ 有区别)，解码器输出 $y_{t^{\prime}}$ 的条件概率可以写成下面的公式：
$P\left(y_{t^{\prime}} \mid y_{1}, \ldots, y_{t^{\prime}-1}, \boldsymbol{c}\right)$
其中 $y_{1}, \ldots, y_{t^{\prime}-1}$ 是当前 $t^{\prime}$ 时刻之前每个时刻的输出， $c$ 就是背景变量。

为此，我们使用另一个循环神经网络作为解码器，在输出序列的时间步 $t^{\prime}$ 解码器将上⼀时间步的输出 $y_{t^{\prime}-1}$ 以及背景变量 $c$ 作为输⼊，并将它们与上⼀时间步的隐藏状态 $s_{t^{\prime}-1}$ 变换为当前时间步的隐藏状态 $s_{t^{\prime}}$ 。因此，我们可以⽤函数 $g$ 表达解码器隐藏层的变换：
$\boldsymbol{s}_{t^{\prime}}=g\left(y_{t^{\prime}-1}, \boldsymbol{c}, \boldsymbol{s}_{t^{\prime}-1}\right)$
有了解码器的隐藏状态后，我们可以使⽤⾃定义的输出层和 softmax 运算来计算 $P\left(y_{t^{\prime}} \mid y_{1}, \ldots, y_{t^{\prime}-1}, \boldsymbol{c}\right)$ ，例如，基于当前时间步的解码器隐藏状态 $s_{t^{\prime}}$ 、上⼀时间步的输出以及 $y_{t^{\prime}-1}$ 背景变量 $c$ 来计算当前时间步输出 $y_{t^{\prime}}$ 的概率分布。

4.注意力机制

我们再来思考上面讲到的例子，对于编码端输入的句子：“They”“are”“watching”“.”，输出为法语序列“Ils”“regardent”“.”。不难想到，解码器在⽣成输出序列中的每⼀个词时可能只需利⽤输⼊序列某⼀部分的信息。例如，在输出序列的时间步1，解码器可以主要依赖“They”“are”的信息来⽣成“Ils”，在时间步2则主要使⽤来⾃“watching”的编码信息⽣成“regardent”，最后在时间步3则直接映射句号“.”。这看上去就像是在解码器的每⼀时间步对输⼊序列中不同时间步的表征或编码信息分配不同的注意⼒⼀样。这也是注意⼒机制的由来。

仍然以循环神经⽹络为例，注意⼒机制通过对编码器所有时间步的隐藏状态做加权平均来得到背景变量。解码器在每⼀时间步调整这些权重，即注意⼒权重，从⽽能够在不同时间步分别关注输⼊序列中的不同部分并编码进相应时间步的背景变量。下面会讨论注意力是怎么工作的。

在开始之前我们再来明确一些变量的含义。为了区分了输⼊序列或编码器的索引 $t$ 与输出序列或解码器的索引 $t^{\prime}$ 。我们定义在解码器在时间步 $t^{\prime}$ 的隐藏状态 $\boldsymbol{s}_{t^{\prime}}=g\left(\boldsymbol{y}_{t^{\prime}-1}, \boldsymbol{c},\boldsymbol{s}_{t^{\prime}-1}\right)$ ，其中 $\boldsymbol{y}_{t^{\prime}-1}$ 是上个时间步 $t^{\prime}-1$ 的输出的表征 $y_{t^\prime-1}$ ，且任⼀时间步 $t^{\prime}$ 使⽤相同的背景变量 $\boldsymbol{c}$ 。但在注意⼒机制中，解码器的每⼀时间步将使⽤可变的背景变量。记 $\boldsymbol{c}_{t^{\prime}}$ 是解码器在时步 $t^{\prime}$ 的背景变量，那么解码器在该时间步的隐藏状态可以改写为:
$\boldsymbol{s}_{t^{\prime}}=g\left(\boldsymbol{y}_{t^{\prime}-1}, \boldsymbol{c}_{t^{\prime}}, \boldsymbol{s}_{t^{\prime}-1}\right)$
这⾥的关键是如何计算背景变量 $\boldsymbol{c}_{t^{\prime}}$ 和如何利⽤它来更新隐藏状态 $\boldsymbol{s}_{t^{\prime}}$ 。下⾯将分别描述这两个关键点。

4.1计算背景变量

图2描绘了注意⼒机制如何为解码器在时间步2计算背景变量。⾸先，函数 $a$ 根据解码器在时间步1的隐藏状态和编码器在各个时间步的隐藏状态计算softmax运算的输⼊。softmax运算输出概率分布并对编码器各个时间步的隐藏状态做加权平均，从⽽得到背景变量。

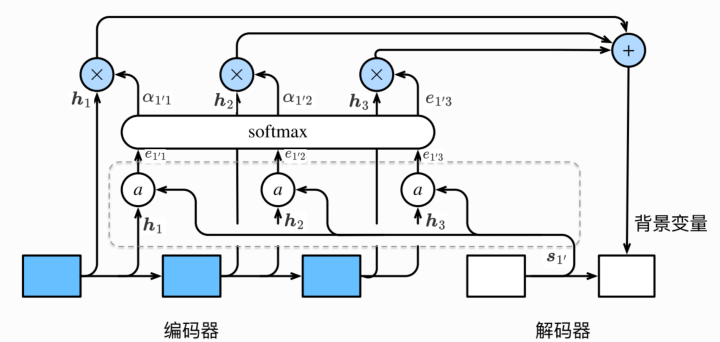
图2 编码器-解码器上的注意力机制

在这里笔者不想用列举公式的方式来讲解，换一种方式。图2看起来可能有些乱，但是我劝读者您的心不要乱，来跟着我的视线一起看，图中的分叉流程都是向量的复制操作。

step1、先看图中被虚线框住的部分， $\boldsymbol{h}_{1}$ 、 $\boldsymbol{h}_{2}$ 、 $\boldsymbol{h}_{3}$ 是编码器三个时间步的输出隐状态，如果我们按照每批次只输入一个句子，经过循环神经网络单元计算之后，三者是等长的向量，同理 $\boldsymbol{s}_{1^{\prime}}$ 亦是，三个 $a$ 的操作分别是 $\boldsymbol{s}_{1^{\prime}}$ · $\boldsymbol{h}_{1}^{\top}$ 、 $\boldsymbol{s}_{1^{\prime}}$ · $\boldsymbol{h}_{2}^{\top}$ 、 $\boldsymbol{s}_{1^{\prime}}$ · $\boldsymbol{h}_{3}^{\top}$ ，这是矩阵乘法，也是两个向量的内积，所以每个计算结果都是一个实数，分别用 $e_{1^{\prime} 1}$ 、 $e_{1^{\prime} 2}$ 、 $e_{1^{\prime} 3}$ 来表示，把三者做softmax操作就会得到解码端在时刻2需要的背景向量对应编码端每个时刻注意力权重，经过softmax后得到三个权重分别是 $\alpha_{1^{\prime} 1}$ 、 $\alpha_{1^{\prime} 2}$ 、 $\alpha_{1^{\prime} 3}$ ；

step2、继续看图上方的三个✖️，该乘号是数学乘法，拿其中一个乘号举例子，比如向量 $\boldsymbol{h}_{1}$ ，就是把它的每一个元素都与 $\alpha_{1^{\prime} 1}$ 相乘，得到的也是一个向量，其他的两个乘号也是分别与其对应的权重参数做如此操作；

step3、最后看右上角的➕，到此就很简单了，把上一步得到的三个结果向量对位相加即得到解码端第2个时间步需要的背景向量 $\boldsymbol{c}_{2^{\prime}}$ 。

解码器其它时间步需要的背景向量也是按照上述过程计算得到。

说到这里不得不对第一步中的 $a$ 函数做一个补充，试想如果 $\boldsymbol{s}_{1^{\prime}}$ 与 $\boldsymbol{h}_{1}$ 、 $\boldsymbol{h}_{2}$ 、 $\boldsymbol{h}_{3}$ 的向量长度不同，无法做向量内积，该怎么办呢？此时，就写一个简单的公式来解决。
$a(\boldsymbol{s}, \boldsymbol{h})=\boldsymbol{v}^{\top} \tanh \left(\boldsymbol{W}_{s} \boldsymbol{s}+\boldsymbol{W}_{h} \boldsymbol{h}\right)$
即把编码器和解码器的输出分别与两个参数矩阵相乘，转化为同一维度，再做计算。其中 $v$ 、 $W_{s}$ 、 $W_{h}$ 都是可以学习的参数。（下面的代码对该公式进行了实现）

5.代码实战

拒绝纸上谈兵，一起代码实战。

导入必要的一些包。

import collections
import os
import io
import math
import torch
from torch import nn
import torch.nn.functional as F
import torchtext.vocab as Vocab
import torch.utils.data as Data
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
# PAD：我们在训练模型时是按照批次进行了，句子长短不一，用PAD填补短句子到指定长度。
PAD, BOS, EOS = '<pad>', '<bos>', '<eos>'
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

定义两个辅助函数对后面读取的数据做预处理。

# 将⼀个序列中所有的词记录在all_tokens中以便之后构造词典，然后在该序列后⾯添加PAD直到序列
# ⻓度变为max_seq_len，然后将序列保存在all_seqs中
def process_one_seq(seq_tokens, all_tokens, all_seqs, max_seq_len):
		all_tokens.extend(seq_tokens)
		seq_tokens += [EOS] + [PAD] * (max_seq_len - len(seq_tokens) - 1)
		all_seqs.append(seq_tokens)
# 使⽤所有的词来构造词典。并将所有序列中的词变换为词索引后构造Tensor
def build_data(all_tokens, all_seqs):
		vocab = Vocab.Vocab(collections.Counter(all_tokens), specials=[PAD, BOS, EOS])
		indices = [[vocab.stoi[w] for w in seq] for seq in all_seqs]
		return vocab, torch.tensor(indices)

为了演示⽅便，我们在这⾥使⽤⼀个很⼩的法语—英语数据集（其实只有两句话）。在这个数据集⾥，每⼀⾏是⼀对法语句⼦和它对应的英语句⼦，中间使⽤ ‘\t’ 隔开。在读取数据时，我们在句末附上“”符号，并可能通过添加“”符号使每个序列的⻓度均为 max_seq_len 。我们为法语词和英语词分别创建词典。法语词的索引和英语词的索引相互独⽴。

def read_data(max_seq_len):
		# in和out分别是input和output的缩写
		in_tokens, out_tokens, in_seqs, out_seqs = [], [], [], []
		with io.open('../../data/fr-en-small.txt') as f:
				lines = f.readlines()
		for line in lines:
				in_seq, out_seq = line.rstrip().split('\t')
				in_seq_tokens, out_seq_tokens = in_seq.split(' '), out_seq.split(' ')
				if max(len(in_seq_tokens), len(out_seq_tokens)) > max_seq_len - 1:
						continue # 如果加上EOS后⻓于max_seq_len，则忽略掉此样本
				process_one_seq(in_seq_tokens, in_tokens, in_seqs, max_seq_len)
				process_one_seq(out_seq_tokens, out_tokens, out_seqs, max_seq_len)
		in_vocab, in_data = build_data(in_tokens, in_seqs)
		out_vocab, out_data = build_data(out_tokens, out_seqs)
		return in_vocab, out_vocab, Data.TensorDataset(in_data, out_data)

将序列的最⼤⻓度设成7，然后查看读取到的第⼀个样本。该样本分别包含法语词索引序列和英语词索引序列。

max_seq_len = 7
in_vocab, out_vocab, dataset = read_data(max_seq_len)
dataset[0]

下面我们使用pytorch实现编码端。

class Encoder(nn.Module):
		def __init__(self, vocab_size, embed_size, num_hiddens, num_layers, drop_prob=0, **kwargs):
				super(Encoder, self).__init__(**kwargs)
				# 将输⼊语⾔的词索引通过词嵌⼊层得到词的表征
				self.embedding = nn.Embedding(vocab_size, embed_size)
				# 这里我们在初始化的时候，没有指定第一个维度为batch_size，所以在输入rnn时，
				# 应该是个（seq_len, batch_size, embed_size）形状的张量
				self.rnn = nn.GRU(embed_size, num_hiddens, num_layers, dropout=drop_prob)
		def forward(self, inputs, state):
				# 输⼊形状是(批量⼤⼩, 时间步数)。将输出互换样本维和时间步维
				embedding = self.embedding(inputs.long()).permute(1, 0, 2)
				# (seq_len, batch, input_size)
				return self.rnn(embedding, state)
		def begin_state(self):
				return None # 隐藏态初始化为None时PyTorch会⾃动初始化为0

下⾯我们来创建⼀个批量⼤⼩为4、时间步数为7的⼩批量序列输⼊。设⻔控循环单元的隐藏层个数为2，隐藏单元个数为16。编码器对该输⼊执⾏前向计算后返回的输出形状为(时间步数, 批量⼤⼩, 隐藏单元个数)。⻔控循环单元在最终时间步的多层隐藏状态的形状为(隐藏层个数, 批量⼤⼩, 隐藏单元个数)。对于⻔控循环单元来说， state 就是⼀个元素，即隐藏状态；如果使⽤⻓短期记忆， state 是⼀个元组，包含两个元素即隐藏状态和记忆细胞。

encoder = Encoder(vocab_size=10, embed_size=8, num_hiddens=16, num_layers=2)
output, state = encoder(torch.zeros((4, 7)), encoder.begin_state())
output.shape, state.shape # GRU的state是h, ⽽LSTM的是⼀个元组(h, c)
# 输出：(torch.Size([7, 4, 16]), torch.Size([2, 4, 16]))

这里我们实现公式6中的注意力机制。

def attention_model(input_size, attention_size):
		model = nn.Sequential(nn.Linear(input_size,                                      attention_size,bias=False),nn.Tanh(),nn.Linear(attention_size, 1, bias=False))
		return model

接下来就是带有注意力机制的背景向量计算过程了。

def attention_forward(model, enc_states, dec_state):
		"""
		model:函数attention_model返回的模型
 		enc_states: 编码端的输出，shape是(时间步数, 批量⼤⼩, 隐藏单元个数)
 		dec_state: 解码端一个时间步的输出，shape是(批量⼤⼩, 隐藏单元个数)
 		"""
		# 将解码器隐藏状态⼴播到和编码器隐藏状态形状相同后进⾏连结
		dec_states = dec_state.unsqueeze(dim=0).expand_as(enc_states)
		# 形状为(时间步数, 批量⼤⼩, 1)
		enc_and_dec_states = torch.cat((enc_states, dec_states), dim=2) 
		e = model(enc_and_dec_states) # 这里的model是上面attention_model函数的返回值
		alpha = F.softmax(e, dim=0) # 在时间步维度做softmax运算
		return (alpha * enc_states).sum(dim=0) # 返回背景变量

在这里我们随机个案例，对以上代码做个测试，编码器的时间步数为10，批量⼤⼩为4，编码器和解码器的隐藏单元个数均为8。注意⼒机制返回⼀个⼩批量的背景向量，每个背景向量的⻓度等于编码器的隐藏单元个数。因此输出的形状为(4, 8)。

seq_len, batch_size, num_hiddens = 10, 4, 8
model = attention_model(2*num_hiddens, 10)
enc_states = torch.zeros((seq_len, batch_size, num_hiddens))
dec_state = torch.zeros((batch_size, num_hiddens))
attention_forward(model, enc_states, dec_state).shape # torch.Size([4, 8])

下面来实现带有注意力机制的解码端。

本代码中把编码器在最终时间步的隐藏状态作为解码器的初始隐藏状态。这要求编码器和解码器的循环神经⽹络使⽤相同的隐藏层个数和隐藏单元个数。

在解码器的前向计算中，我们先通过刚刚介绍的注意⼒机制计算得到当前时间步的背景向量。由于解码器的输⼊来⾃输出语⾔的词索引，我们将输⼊通过词嵌⼊层得到表征，然后和背景向量在特征维连结。我们将连结后的结果与上⼀时间步的隐藏状态通过⻔控循环单元计算出当前时间步的输出与隐藏状态。最后，我们将输出通过全连接层变换为有关各个输出词的预测，形状为(批量⼤⼩, 输出词典⼤⼩)。

class Decoder(nn.Module):
		def __init__(self, vocab_size, embed_size, num_hiddens, num_layers, attention_size, drop_prob=0):
				super(Decoder, self).__init__()
				self.embedding = nn.Embedding(vocab_size, embed_size)
				self.attention = attention_model(2*num_hiddens, attention_size)
				# GRU的输⼊包含attention输出的c和实际输⼊, 所以尺⼨是2*embed_size
				self.rnn = nn.GRU(2*embed_size, num_hiddens, num_layers, dropout=drop_prob)
				self.out = nn.Linear(num_hiddens, vocab_size)
		def forward(self, cur_input, state, enc_states):
				"""
				cur_input shape: (batch, )
				state shape: (num_layers, batch, num_hiddens)
				"""
				# 使⽤注意⼒机制计算背景向量
				c = attention_forward(self.attention, enc_states, state[-1])
				# 将嵌⼊后的输⼊和背景向量在特征维连结
				input_and_c = torch.cat((self.embedding(cur_input), c), dim=1) # (批量⼤⼩, 2*embed_size)
				# 为输⼊和背景向量的连结增加时间步维，时间步个数为1
				output, state = self.rnn(input_and_c.unsqueeze(0), state)
				# 移除时间步维，输出形状为(批量⼤⼩, 输出词典⼤⼩)
				output = self.out(output).squeeze(dim=0)
				return output, state
		def begin_state(self, enc_state):
				# 直接将编码器最终时间步的隐藏状态作为解码器的初始隐藏状态
				return enc_state

在编码器、注意力和解码器实现的基础上，下面我们开始编写训练程序。我们先实现 batch_loss 函数计算⼀个⼩批量的损失。解码器在最初时间步的输⼊是特殊字符 BOS 。之后，解码器在某时间步的输⼊为样本输出序列在上⼀时间步的词，即强制教学。此外，我们在这⾥也使⽤掩码变量避免填充项对损失函数计算的影响。

def batch_loss(encoder, decoder, X, Y, loss):
		batch_size = X.shape[0]
		enc_state = encoder.begin_state()
		enc_outputs, enc_state = encoder(X, enc_state)
		# 初始化解码器的隐藏状态
		dec_state = decoder.begin_state(enc_state)
		# 解码器在最初时间步的输⼊是BOS
		dec_input = torch.tensor([out_vocab.stoi[BOS]] * batch_size)
		# 我们将使⽤掩码变量mask来忽略掉标签为填充项PAD的损失
		mask, num_not_pad_tokens = torch.ones(batch_size,), 0 
		l = torch.tensor([0.0])
		for y in Y.permute(1,0): # Y shape: (batch, seq_len)
				dec_output, dec_state = decoder(dec_input, dec_state, enc_outputs) 
        l = l + (mask * loss(dec_output, y)).sum()
				dec_input = y # 使⽤强制教学
				num_not_pad_tokens += mask.sum().item()
			# 将PAD对应位置的掩码设成0,
				mask = mask * (y != out_vocab.stoi[PAD]).float()
		return l / num_not_pad_tokens

在训练函数中，我们需要同时迭代编码器和解码器的模型参数。

def train(encoder, decoder, dataset, lr, batch_size, num_epochs):
		enc_optimizer = torch.optim.Adam(encoder.parameters(), lr=lr)
		dec_optimizer = torch.optim.Adam(decoder.parameters(), lr=lr)
		loss = nn.CrossEntropyLoss(reduction='none')
		data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
		for epoch in range(num_epochs):
				l_sum = 0.0
				for X, Y in data_iter:
						enc_optimizer.zero_grad()
						dec_optimizer.zero_grad()
						l = batch_loss(encoder, decoder, X, Y, loss) 
						l.backward()
						enc_optimizer.step()
						dec_optimizer.step()
						l_sum += l.item()
				if (epoch + 1) % 10 == 0:
						print("epoch %d, loss %.3f" % (epoch + 1, l_sum / len(data_iter)))

接下来，创建模型实例并设置超参数。然后，我们就可以训练模型了。

embed_size, num_hiddens, num_layers = 64, 64, 2
attention_size, drop_prob, lr, batch_size, num_epochs = 10, 0.5, 0.01, 2, 50
encoder = Encoder(len(in_vocab), embed_size, num_hiddens, num_layers, drop_prob)
decoder = Decoder(len(out_vocab), embed_size, num_hiddens, num_layers, attention_size, drop_prob)
train(encoder, decoder, dataset, lr, batch_size, num_epochs)

原文链接：https://blog.csdn.net/KaikebaAI/article/details/121141276