基于源代码:《机器学习——支持向量机SVM之python实现简单实例一》进行讲解
1、线性模型
这里以二特征三类,一对多策略为案例
kernel = “linear”:线性核,参数有w,b
线性模型的决策边界是:w0iTx0i + w1iTx1i + bi = 0
注:w0iTx0i + w1iTx1i + bi = 1和w0iTx0i + w1iTx1i + bi = -1是穿过支持向量的决策面,边界
i的大小由类别的个数决定,i = n,说明决策函数有n个,因此查看参数的时候,w为一个nx2的数组,2代表的是特征的个数
classifier=svm.SVC(C=100,kernel='linear',gamma=100,decision_function_shape='ovr') # ovr:一对多策略
classifier.coef_#参数w
#[[-6.28425012 5.14207649]
[-8.45820407 6.92112224]
[-0.99813811 -2.00212539]]
classifier.intercept_#参数b
# [-0.07076934 -0.08011805 0.12861107]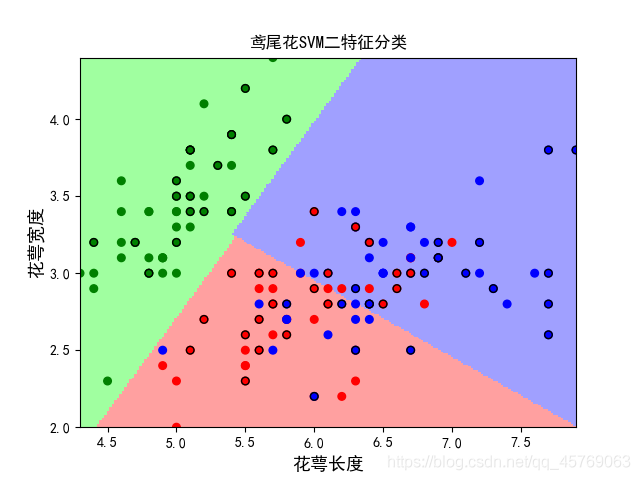
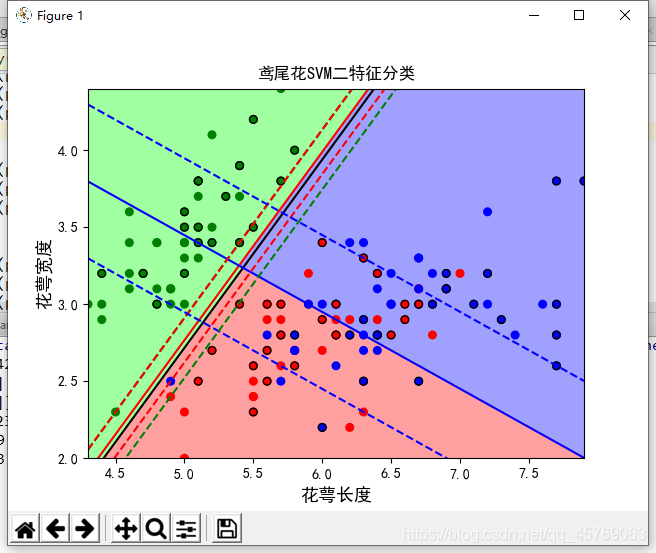
图中实线为分界面,虚线为决策边界,穿过支持向量的边界
#绘制边界和分界面
def plot_boundary(w,b):
plot_x1 = np.linspace(x[:, 0].min(), x[:, 0].max(), 200)
#分界面w0x0 + w1x1 + b = 0
plot_x21 = -w[0][0] / w[0][1] * plot_x1 - b[0] / w[0][1]
plot_x31 = -w[1][0] / w[1][1] * plot_x1 - b[1] / w[1][1]
plot_x41 = -w[2][0] / w[2][1] * plot_x1 - b[2] / w[2][1]
#上边界w0x0 + w1x1 + b = 1
plot_up_x21 = -w[0][0] / w[0][1] * plot_x1 - b[0] / w[0][1] + 1/w[0][1]
plot_up_x31 = -w[1][0] / w[1][1] * plot_x1 - b[1] / w[1][1] + 1/w[1][1]
plot_up_x41 = -w[2][0] / w[2][1] * plot_x1 - b[2] / w[2][1] + 1/w[2][1]
#下边界w0x0 + w1x1 + b = -1
plot_down_x21 = -w[0][0] / w[0][1] * plot_x1 - b[0] / w[0][1] - 1/w[0][1]
plot_down_x31 = -w[1][0] / w[1][1] * plot_x1 - b[1] / w[1][1] - 1/w[1][1]
plot_down_x41 = -w[2][0] / w[2][1] * plot_x1 - b[2] / w[2][1] - 1/w[2][1]
#分界面
plt.plot(plot_x1, plot_x21, c="black")
plt.plot(plot_x1, plot_x31, "r")
plt.plot(plot_x1, plot_x41, c="b")
#上边界
plt.plot(plot_x1, plot_up_x21, "g--")
plt.plot(plot_x1, plot_up_x31, "r--")
plt.plot(plot_x1, plot_up_x41, "b--")
#上边界
plt.plot(plot_x1, plot_down_x21, "g--")
plt.plot(plot_x1, plot_down_x31, "r--")
plt.plot(plot_x1, plot_down_x41, "b--")
plot_boundary(w,b)其中:
w=ceof_:
[[-6.28425012 5.14207649]
[-8.45820407 6.92112224]
[-0.99813811 -2.00212539]]
b=intercept_:
[17.45202353 23.14272776 11.8943489 ]
2、非线性模型
非线性模型使用的是高斯核,kernel = “rbf”,参数有:b
,w不需要计算
classifier=svm.SVC(C=100,kernel='rbf',gamma=100,decision_function_shape='ovr') # ovr:一对多策略
classifier.intercept_#参数b
# [-0.07076934 -0.08011805 0.12861107]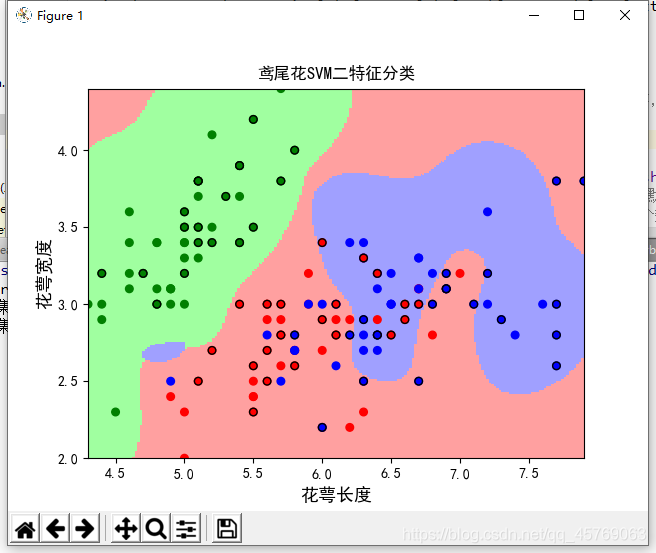
版权声明:本文为qq_45769063原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。