大整数

1.大整数加法

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<map>
#include<vector>
#include<cstring>
#include<cmath>
#include<iomanip>
#include<ctime>
#include<cstdlib>
#include<stack>
#include<queue>
using namespace std;
#define max_n 1000
char str1[max_n], str2[max_n];
int num1[max_n], num2[max_n];



int main() {
    memset(str1, 0, sizeof(str1));
    memset(str2, 0, sizeof(str2));
    memset(num1, 0, sizeof(num2));
    memset(num2, 0, sizeof(num2));
    scanf("%s%s", str1, str2);
    int len1 , len2;
    len1 = strlen(str1);
    len2 = strlen(str2);
    int j = 0;
    int max = len1 > len2 ? len1 : len2;//取长度最大的赋值给max
    for (int i = len1 - 1 ;i >= 0 ;i--) 
    num1[j++] = str1[i] - '0';
  	//到过来存储
    j = 0;
    for (int i = len2 - 1 ;i >= 0 ;i--) 
    num2[j++] = str2[i] - '0';
  	//到过来存储
    for (int i = 0 ;i < max; i++) {//以最长的长度为基准
        num2[i] += num1[i];
        if (num2[i] >= 10) {
            num2[i] -= 10;
            num2[i + 1] += 1;
        }
    }
    if (num2[max]) printf("%d", num2[max]);
    for (int i = max - 1;i >= 0; i--) {
        printf("%d", num2[i]);
    }
    printf("\n");
    return 0;
}

代码解析

1.第一种要注意到的就是位数不想等的情况，所以我门要先对齐位数，再去模仿竖式

​ 就用 int max = len1 > len2 ? len1 : len2

2.做完之后将数字到着存在数组中，为了方便思考。

3.之后就是核心思想进位 10位进1， 向下一位进，这就是到这存储的原因

2.大整数减法

思想就是比大整数加法繁琐一点

最主要的一点就是大整数减法是要去借位，去向上一位借1位， 上一位减一位

#include <iostream>
#include <vector>
#include <iomanip>
#include <map>
#include <queue>
#include <stack>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <algorithm>
using namespace std;

string str1, str2, str3;
int aa[1005], bb[1005], cc[1005], la, lb, lc;

int main(){
    cin >> str1 >> str2;
    la = str1.size();
    lb = str2.size();
    if(la < lb || ((la == lb) && (str1 < str2))){
        str3 = str2;
        str2 = str1;
        str1 = str3;
        cout << "-";
    }

    la = str1.size();
    lb = str2.size();
    for(int i = 0; i < la; i++){
        aa[i] = str1[la - i -1] - '0';
    }

    for(int i = 0; i < lb; i++){
        bb[i] = str2[lb - i -1] - '0';
    }
    int k = 0;
    for(int i = 0; i < la; i++){
        k = aa[i] - bb[i];
        if(k < 0){
            k += 10;
            aa[i + 1] -= 1;
        }
        cc[i] = k;
    }

    while(cc[la] == 0) la--;
    for(int i = la; i >= 0 ; i--){
        cout << cc[i];
    }
    cout << endl;
    return 0;
}

3.大整数乘法

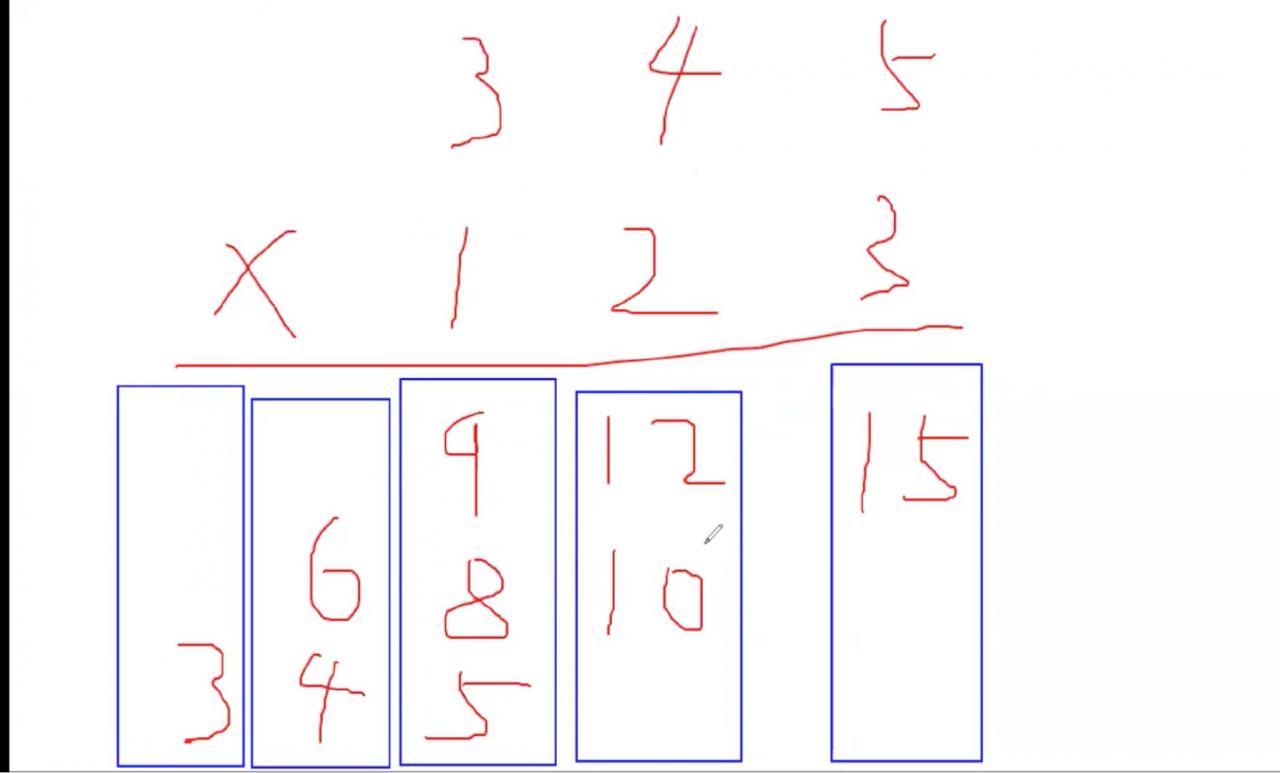
模拟竖式，将乘的结果放在数组中，最后处理一下今进位的问题

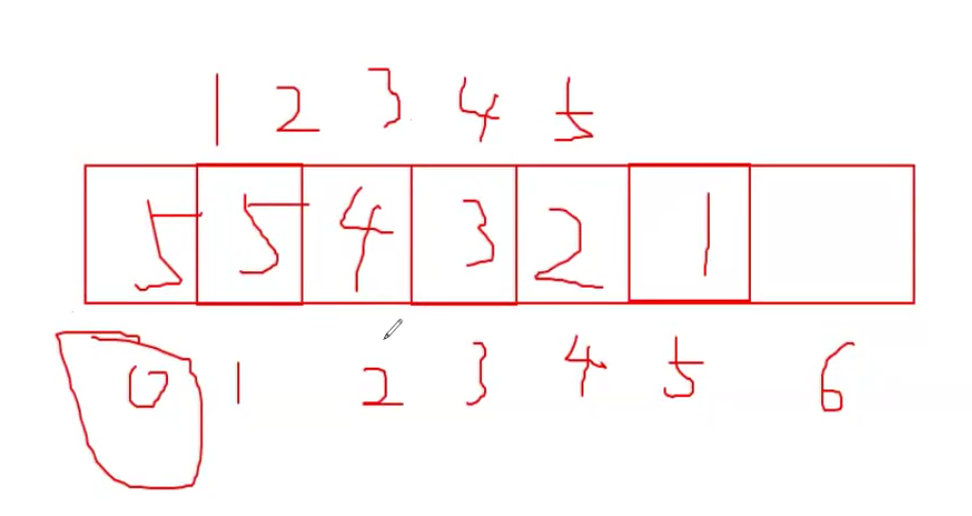
数组的0位是长度，倒着存储。

#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
#include <queue>
#include <map>
#include <stack>
#include <cstring>
#include <cmath>
#include <ctime>
using namespace std;
char num1[105], num2[105];
int num3[105], num4[105], ans[305];
//用数组的0位去存长度可以节省i部分的空间
int main() {
    cin >> num1 >> num2;
    for (int i = strlen(num1) - 1, j = 1; i >= 0; i--, j++) {
        num3[j] = num1[i] - '0';
    }
    for (int i = strlen(num2) - 1, j = 1; i >= 0; i--, j++) {
        num4[j] = num2[i] - '0';
    }
    num3[0] = strlen(num1);
    num4[0] = strlen(num2);
    for (int i = 1; i <= num3[0]; i++) {
        for (int j = 1; j <= num4[0]; j++) {
            ans[i + j - 1] += num3[i] * num4[j];
        }
    }
  //核心思想
    for (int i = 1; i <= num3[0] + num4[0]; i++) {
        if (ans[i] >= 10) {
            ans[i + 1] += ans[i] / 10;
            ans[i] %= 10;
        }
        if (ans[i] != 0) {
            ans[0] = i;
        }
    }
    for (int i = ans[0]; i > 0; i--) {
        cout << ans[i];
    }
    cout << endl;
    return 0;
}

4.大整数除法

1.模拟竖式，每次判断当前缓存是否大于除数

2.若大于则减去一次除数，答案加一 并继续判断

3.若不是则将除数的下一位加入缓存 同时答案进一位 并继续判断

4.直到被除数全部加入缓存 且缓存不大于除数

5.此时答案即为商 缓存即为余数