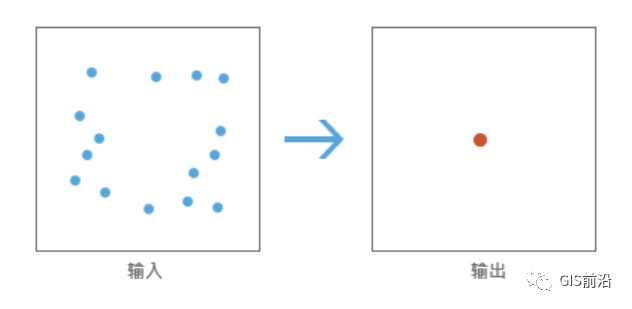
概述：

识别一组要素的地理中心(或密度中心)。

 

公式：

平均中心可表示为：

 

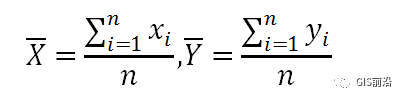
其中xi 和yi 是要素i的坐标，n等于要素总数。召权平均中心扩展为：

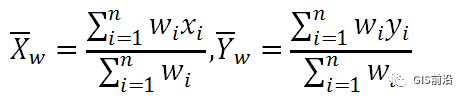
其中wi 为要素i处的权重。如果各要素存在z属性，则该工具还会计算

第三维的中心:

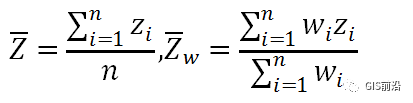
说明：

平均中心工具会创建一个新的点要素类，要素类中的每个要素表示一个平均中心(如果您指定了案例分组字段，则每个案例都会对应一个平均中心)。X 和 Y 平均中心值、案例及平均尺寸字段都将作为属性包含在输出要素类内。尺寸字段可以是数据集中的任一数值型字段；输出要素类中的“尺寸”值是该字段所有值的平均值。

中位数中心

概述：

识别使数据集中要素之间的总欧氏距离达到最小的位置点。

 

公式：

 

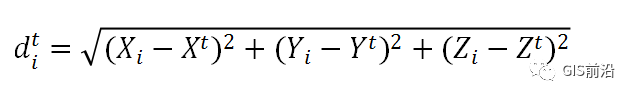
说明：

中位数中心工具是一种对异常值反应较为稳健的中心趋势的量度。该工具可标识数据集中到其他所有要素的行程最小的位置点。例如，对紧凑性群集点的平均中心进行计算的结果是该群集中心处的某个位置点。如果随后添加一个远离该群集的新点并重新进行计算平均中心，您会注意到结果会向新的异常值靠近。

试验

在我们的实际研究中，平均中心和中位数中心都是我们经常用到的工具，但是我们很少单独拿出来用，因为在我们使用比如标准距离、方向分布等工具的时候，会自动生成一个中心，那个中心其实就是平均数中心，然而虽然平均中心和中位数中心均是中心趋势度量。但是，相比而言， 中位数中心工具的算法受数据异常值的影响较小。

我们以实际例子来看看平均中心与中位数中心有何区别：

我们以粤港澳大湾区为例，以密密麻麻的交通信号灯点数据为分析数据，数据源来自OSM：

 

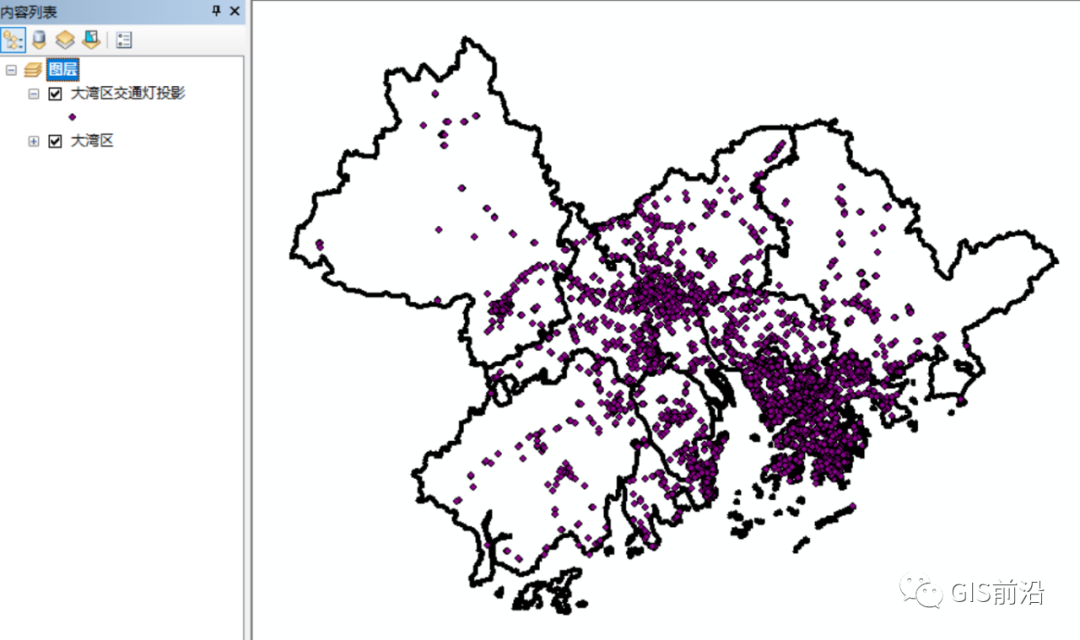
在Spatial Statistics Tools中的度量地理分布-平均中心和中位数中心可以找到：

 

先看平均中心，其实需要输入的参数蛮少，我们只需载入数据，如果你需要生成不同类的中心，那么你就需要在案例分组字段中设置那个需要分类的字段，这里我们选择默认：

 

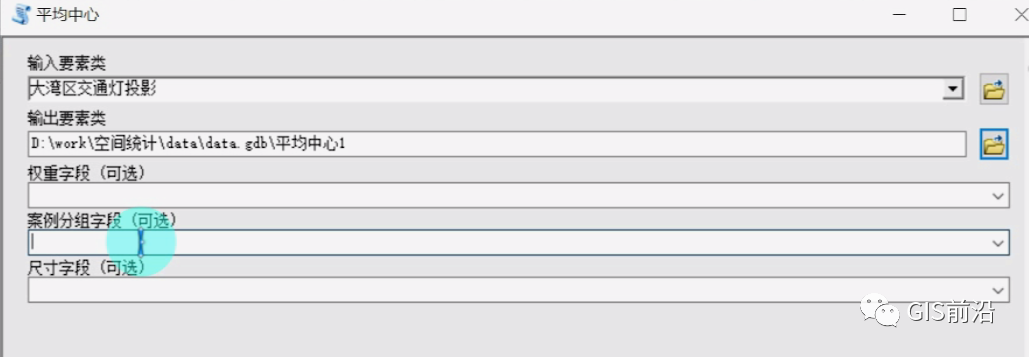
很明显，如果你还记得之前的标准距离和方向分布，那么这个平均中心的坐标就是那个圆心的坐标：

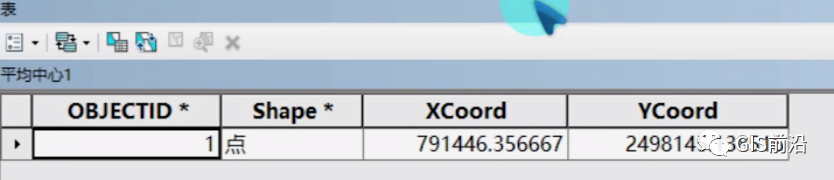
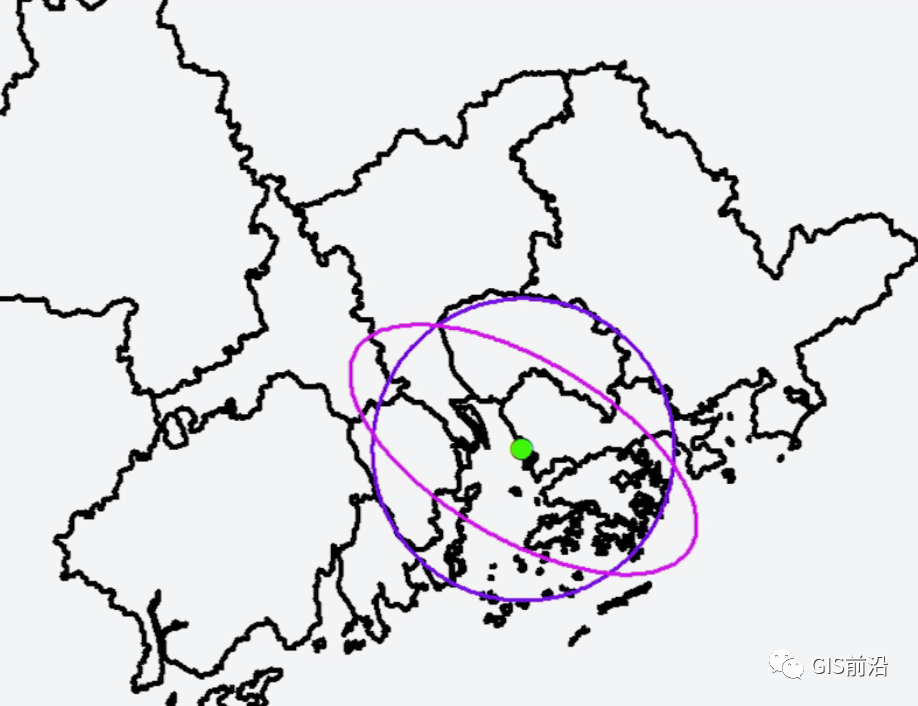
就是如此的工作原理，因此在实际工作中我们不需要特意的去找出这个中心在哪，因为你需要描述数据分布的时候，采用的工具一般都会生成这个平均中心。

然后我们来看看中位数中心，前面已经提到，如果你的数据有非常多的极端值(在你需要考虑要素的属性的时候)，那么其实平均中心并不是一个非常好的选择，中位数中心显得更加适合，我们打开中位数中心的界面，发现多处了一个属性字段的选择：

 

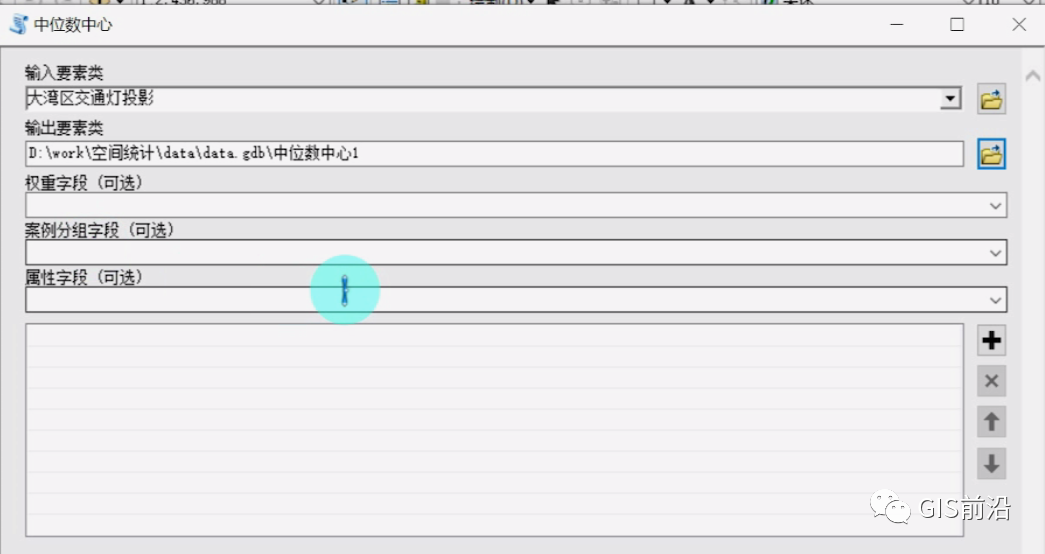
言下之意也就很明显了，如果你要考虑数据的属性，再去考察它的分布，比如说某些事物的价格，就比如说路灯，我认为中心城市的路灯质量好一些，价格贵一些，那么此时你考虑它的价格属性，就需要将之添加到属性字段当中，否则出来的还是只考虑了位置关系的一个中位数中心。有朋友可能会问，如果我仍然选择默认，那么难道出来的点的坐标和平均中心一样吗？答案是不一样~因为这其实跟你的要素的聚集离散程度有关，假如说你的数据非常离散，那么也就意味着你的中位数中心与平均中心差异会非常大，我们从公式的区别就可以看出来了，假如说你的数据非常集聚并且非常庞大，那么其实你的中位数中心与平均中心的位置差异十分的小(在不考虑属性的情况下)，当然也大概率不会重叠，我们这里没有路灯的价格数据，我们选择默认的来看一看与平均中心的区别：

 

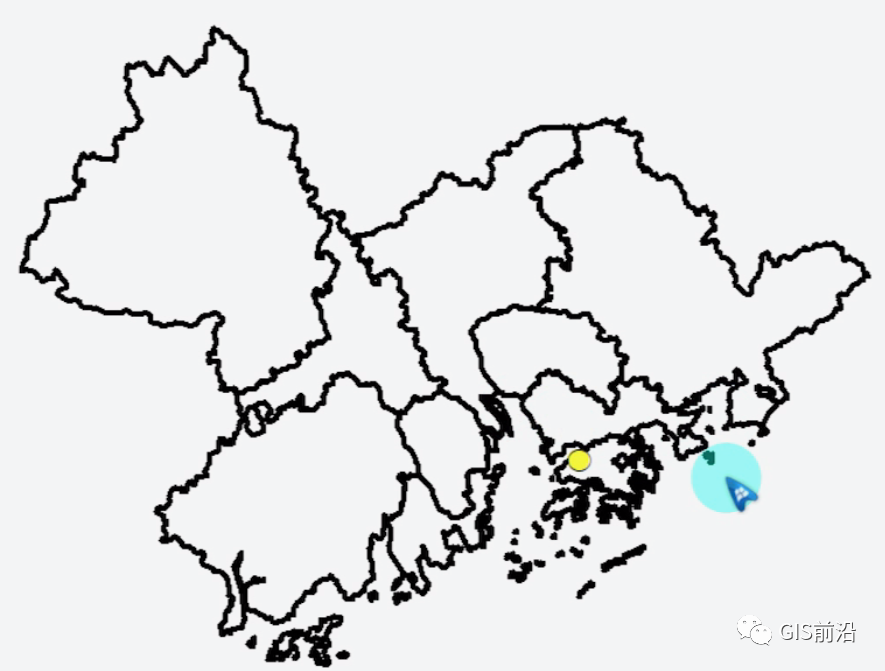
上图黄色的即为中位数中心，我们可以看到大概在香港北部，而平均中心则在深圳的西部：

 

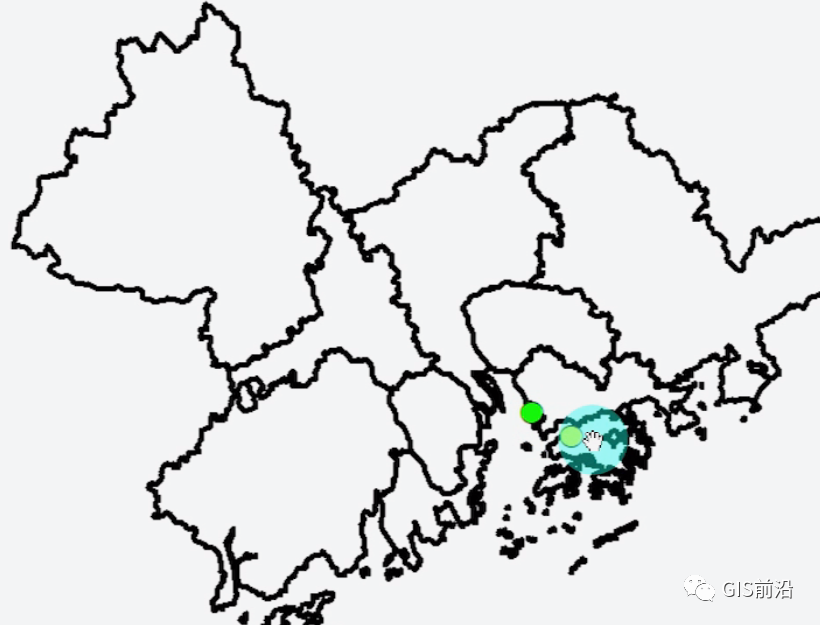
当然了，这是由于我们的数据限制：

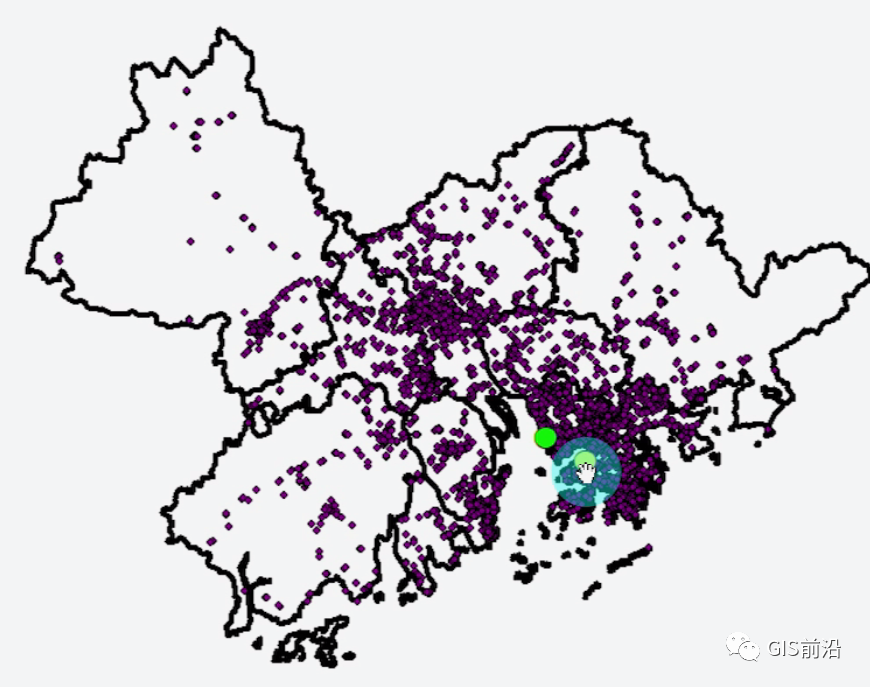
其实我们的数据还是非常庞大并且集聚的(其实我觉得可以算出某种公式，即在只考虑要输位置的情况下，中位数中心与平均中心的差异只要在一个范围内就可以表明数据是空间集聚的，超过了某个范围就是离散的，当然只是猜想)，总之可以看出，我们数据的中位数中心与平均中心空间位置差异还不算大，那么哪种更适合表达呢？在我看来，不考虑数据属性并且要素集聚的情况下，当然还是平均中心啦！

- END -

7.72GB ARCGIS  ERDAS  ENVI干货教程网盘下载 ArcGIS制图技巧—边框的选择 GIS制图人员应该具备制图意识 ArcGIS空间数据分析实用工具——方向分布(标准差椭圆) ArcGIS制图及配图(文档可下载) ArcGIS小白入门——多条件路径规划分析(附练习数据下载)戳原文，更有料！