（1）Frobenius 范数（F-范数）

一种矩阵范数，记为：。

即 矩阵中每项数的平方和的开方值 。

这个范数是针对矩阵而言的，具体定义可以类比 向量的L2范数 。

可用于利用低秩矩阵来近似单一数据矩阵。
用数学表示就是去找一个秩为k的矩阵B，使得矩阵B与原始数据矩阵A的差的 F范数尽可能地小 。

（2）Minkowski-P范数（矩阵元范数？）

当p=1时，就是 曼哈顿距离 （Manhattan distance）， L1距离。
当p=2时，就是 欧氏距离 （Euclidean distance）， L2距离。
当p→∞时，就是 切比雪夫距离（ Chebyshev distance ）。

闵可夫斯基距离比较直观，但是它 与数据的分布无关 ，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就会 过度放大 x 维度 的作用。所以，在计算距离之前，我们可能还需要对数据进行 z-transform 处理，即 减去均值，除以标准差 ：

可以看到，上述处理开始体现数据的统计特性了。

这种方法在假设数据 各个维度不相关 的情况下利用数据分布的特性计算出不同的距离。

如果 维度相互之间数据相关 （例如：身高较高的信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到 马氏距离（Mahalanobis distance） 了。

p-范数 ：，即向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

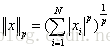
弗罗贝尼乌斯范数（Frobenius norm）是 P范数 在 P=2 时的一种特例，在希尔伯特空间中又叫做希尔伯特-施密特范数（ Hilbert–Schmidt norm），这个范数可用不同的方式定义：

$\|A\|_F=\sqrt{\sum_{i=1}^m\sum_{j=1}^n |a_{ij}|^2}=\sqrt{\operatorname{trace}(A^{{}^*} A)}=\sqrt{\sum_{i=1}^{\min\{m,\,n\}} \sigma_{i}^2}$

$\Vert A \Vert_{p} = \Big( \sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^p \Big)^{1/p}. \,$

特殊的，当 p=2 时，称为 弗罗贝尼乌斯范数 （Frobenius norm）或 希尔伯特-施密特范数 （ Hilbert–Schmidt norm），不过后面这个术语通常 只用于希尔伯特空间 。这个范数可用不同的方式定义：

$\|A\|_F=\sqrt{\sum_{i=1}^m\sum_{j=1}^n |a_{ij}|^2}=\sqrt{\operatorname{trace}(A^{{}^*} A)}=\sqrt{\sum_{i=1}^{\min\{m,\,n\}} \sigma_{i}^2}$

这里A*表示A的 共轭转置 ，σi是A的奇异值，并使用了迹函数。（转置矩阵仅仅是将矩阵的行与列对换，而 共轭转置矩阵 在将行与列 对换后 还要将每个元素共轭一下，实数矩阵的共轭转置矩阵就是转置矩阵。）

弗罗贝尼乌斯范数与 Kn 上 欧几里得范数 非常类似，来自所有矩阵的空间上一个内积。

弗罗贝尼乌斯-范数是服从乘法的且在数值线性代数中非常有用。这个范数通常比 诱导范数 容易计算。