使用邻接表的目的 : 邻接矩阵是一种不错的存储结构,但是我们发现,对于边数目相对于顶点数目很小的时候,这种结构就对存储空间造成了极大浪费.例如: 由图可知,除了arc[1][0]有权值外,没有其他的弧。这些存储空间都浪费掉了。

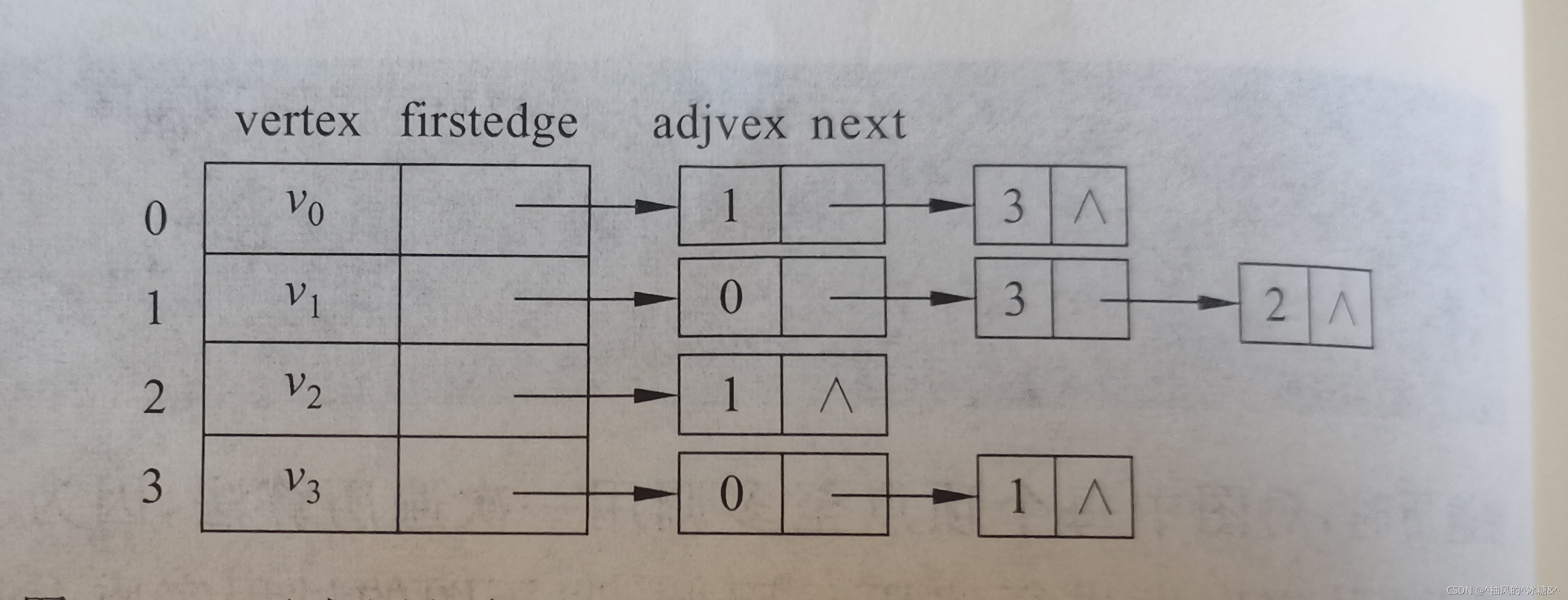
邻接表有两个域,一个是顶点表域,一个是边表域,
定义邻接表结构类型 :
首先看一眼上图,有两个节点域,顶点域和边表域,指针指向的是边表域。
1. 顶点域: 一个vertex变量存储顶点信息, firstedge是一个边表的指针,存放的是边表顶点信息
2.边顶点域: 是由一个一个的顶点由链表链接起来的,这个边表每个顶点都有一个存放顶点信息的adjvex 和指向下一个顶点的next指针。
注意: vertex是顶点域的顶点信息 adjtex是边表域的边表顶点信息
#define MaxVertexNum 100
//定义后面边表的每个顶点的类型
typedef struct ArcNode{
int adjvex; //保存边表顶点的信息
struct ArcNode *next; //用于把边表的顶点连接起来
//inforType info //网的边权值
}ArcNode;
typedef struct VNode{
int vertex; // 定点表中的顶点信息,如V0,V1, V2....
ArcNode *first; //first是ArcNode类型的指针,后面的每一个顶点都是ArcNode类型的节点
}VNode, AdjList[MaxVertexNum];有向图 (网)的邻接表存储示意图 (对于网图,还需要边表结点上定义一个储存权值信息的info域)

定义图类(定义一个顶点表就够了,然后创建结点,把结点插在顶点表的firstedge域
1.确定图的顶点数n 和边数e
2.邻接表有两个域,顶点域和边域,所以分两步初始化
2.1顶点域中,有顶点信息和顶点的指针域,所以用arr[]数组个顶点赋值, 顶点的指针域全部初始化为NULL
2.2边表(无权值):边表有两个信息, 一个是边表顶点信息,一个是边表各顶点的连接,边表不需要初始化,当有新节点插入是,new一个节点,用头插的方式把各个顶点链接成一个链表即可。
void Creat_AdjList(ALGraph G, int n, int e, int arr[]) //创建图, 别忘记用引用
{
G.vexnum=n;
G.arcnum=e;
//初始化顶点表,把arr[]数组中的每个值赋值给顶点表,
for(int i=0; i<G.vexnum; i++)
{
G.vertices[i].vertex = arr[i];
G.vertices[i].firstedge = NULL; //给每一个顶点的边表指针赋值为NULL, 因为还没有添加节点,所以边表是空的
}
//创建无向图 因为是无向图,有a->b的边,就会有b->a的边,所以创建了*s 和 *p指针
for(int i=0; i<G.arcnum; i++)
{
int a,b;
cin>>a>>b; // 表示 a和b有一条边
ArcNode *s = new ArcNode;
s->adjvex = b; //边表的顶点值为 b
s->next = G.vertices[a].firstedge; //用头插法将顶点链接在边表,
G.vertices[a].firstedge = s;
ArcNode *p = new ArcNode;
p->adjvex = a;
p->next = G.vertices[b].firstedge;
G.vertices[b].firstedge = p;
}
}深度优先遍历:
首先指定一个源点v, 从v顶点开始,查找v顶点的邻接点,若邻接点未被访问,则递归进行访问v的邻接点。
void DFSTraverse(ALGraph G, int v)
{
cout<<G.vertices[v].vertex<<" ";
visited[v]=1;
ArcNode *p = G.vertices[v].firstedge;
while(p!=NULL)
{
int j = p->adjvex;
if(visited[j]==0)
{
DFSTraverse(G, j);
}
p = p->next;
}
} 广度优先遍历步骤:
1 .首先需要在外部定义一个队列,遇见一个顶点,先访问,再存放在队列。 2. 队列不为空的时候,先将队列首元素出队,获得当前的下标, 3. 再定义一个移动指针等于这个下标的第一个指针域,利用循环,然后移动这个指针,查看这个结点所有的邻接点。(需要两层循环,一层是当队列不为空的时候,内层循环是用于遍历这个顶点所有的邻接点),当结点有邻接点时候,判断这个邻接点是否被访问过,如果没访问过,那么就访问,并将它入队.如果被访问过,则看下一个邻接点,知道所有的邻接点都查看完,对出内层循环,到外层,从队列中再出队一个元素。
void BFSTraverse(ALGraph G, int v, queue<int> Q)
{
cout<<G.vertices[v].vertex<<" ";
visited[G.vertices[v].vertex] = 1;
Q.push(G.vertices[v].vertex);
while(!Q.empty())
{
int val = Q.front();
Q.pop();
ArcNode *p = G.vertices[val].firstedge;
while(p!=NULL)
{
int j = p->adjvex;
if(!visited[j])
{
cout<<G.vertices[j].vertex<<" ";
visited[j]=1;
Q.push(j);
}
p = p->next;
}
}
}完整代码:
#include<iostream>
using namespace std;
#include<queue>
#define MaxSize 100
typedef struct ArcNode{
int adjvex;
struct ArcNode *next;
//inforType info //网的边权值
}ArcNode;
typedef struct VNode{
int vertex;
ArcNode *firstedge;
}VNode;
typedef struct{
VNode vertices[MaxSize]; //是一个邻接表,有顶点 vertex和边表的first域 v
int vexnum,arcnum; //记录图的顶点个数和边个数。
}ALGraph;
int visited[MaxSize];
void set_visited(ALGraph G)
{
for(int i=0; i<G.vexnum; i++)
{
visited[i]=0;
}
}
void Creat_AdjList(ALGraph &G, int n, int e, int arr[]) //别忘记用引用
{
G.vexnum=n;
G.arcnum=e;
//初始化顶点表,把arr[]数组中的每个值赋值给顶点表,并且顶点表中的每个顶点的first域为NULL
for(int i=0; i<G.vexnum; i++)
{
G.vertices[i].vertex = arr[i];
G.vertices[i].firstedge = NULL;
}
//创建无向图 用头插法链接边表
for(int i=0; i<G.arcnum; i++)
{
int a,b;
cin>>a>>b; // 表示 a->b 有边
ArcNode *s = new ArcNode;
s->adjvex = b;
s->next = G.vertices[a].firstedge;
G.vertices[a].firstedge = s;
ArcNode *p = new ArcNode;
p->adjvex = a;
p->next = G.vertices[b].firstedge;
G.vertices[b].firstedge = p;
}
}
void show_Graph(ALGraph G)
{
for(int i=0; i<G.vexnum; i++)
{
ArcNode *p = G.vertices[i].firstedge;
while(p!=NULL)
{
cout<<"("<<i<<","<<p->adjvex<<")";
p = p->next;
}
cout<<endl;
}
}
void DFSTraverse(ALGraph G, int v)
{
cout<<G.vertices[v].vertex<<" ";
visited[v]=1;
ArcNode *p = G.vertices[v].firstedge;
while(p!=NULL)
{
int j = p->adjvex;
if(visited[j]==0)
{
DFSTraverse(G, j);
}
p = p->next;
}
}
void BFSTraverse(ALGraph G, int v, queue<int> Q)
{
cout<<G.vertices[v].vertex<<" ";
visited[G.vertices[v].vertex] = 1;
Q.push(G.vertices[v].vertex);
while(!Q.empty())
{
int val = Q.front();
Q.pop();
ArcNode *p = G.vertices[val].firstedge;
while(p!=NULL)
{
int j = p->adjvex;
if(!visited[j])
{
cout<<G.vertices[j].vertex<<" ";
visited[j]=1;
Q.push(j);
}
p = p->next;
}
}
}
int main()
{
int n,e;
cin>>n>>e;
int arr[n];
for(int i=0; i<n; i++)
{
cin>>arr[i];
}
queue<int> Q;
ALGraph G;
Creat_AdjList(G,n,e,arr);
set_visited(G);
//show_Graph(G);
BFSTraverse(G,0,Q);
return 0;
}
练习:

5 7
0 1 2 3 4
0 1
0 3
0 4
1 2
1 4
2 3
3 4
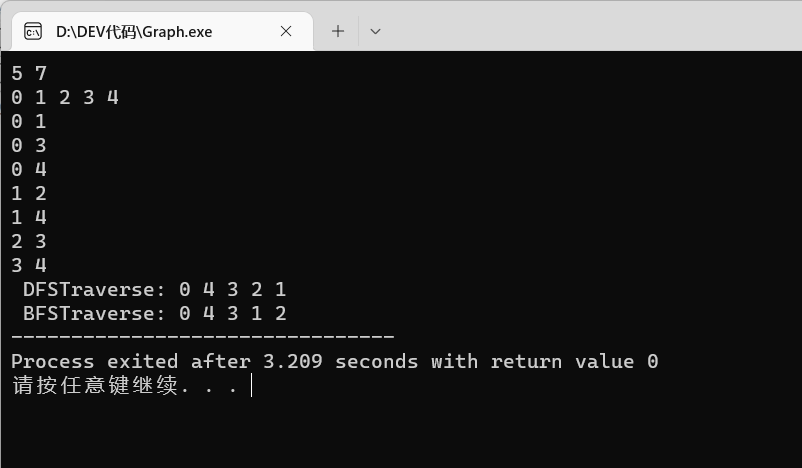
结果并不是按照从小到大的顺序,因为邻接表是链表,插入是无序的,不像邻接矩阵,是按照从小到大的节点挨个查找。