实验原理
1.离散时间信号的时域表示方法
1.1将信号表示成独立时间变量的函数
例如 x[n]=n(0.5)nu[n] 表示一个离散时间信号。在MATLAB中有许多内部函数，可以直接完成信号的这种表达，例如：
sin()：正弦信号
cos()：余弦信号
exp()：指数信号
1.2用信号的波形图来描述信号
用函数曲线表示一个信号，图1.1就是一个连续时间信号和一个离散时间信号的波形图。
图1.1离散时间信号的波形图
1.3将信号用一个数据序列来表示
对于离散时间信号，还可以表示成一个数的序列，例如：
x[n]={...., 0.1, 1.1, -1.2, 0, 1.3, ….}
↑n=0
在《数字信号处理》课程中，上述三种信号的描述方法是经常要使用的。
2．用MATLAB仿真离散时间信号
离散时间信号通常用一个称为样本（Sample）的数字序列来表示，它可以是有限长的或者无限长的。
在MATLAB中，无论是连续时间信号还是离散时间信号，MATLAB都是用一个数字序列来表示信号，这个数字序列在MATLAB中叫做向量(vector)。通常的情况下，需要与时间变量相对应。
如前所述，MATLAB有很多内部数学函数可以用来产生这样的数字序列，例如sin()、cos()、exp()等函数可以直接产生一个按照正弦、余弦或指数规律变化的数字序列。
2.1典型离散时间信号
单位冲激序列（Unit Sample Sequence）
单位冲激序列定义为
（1.1）
移位的单位冲激序列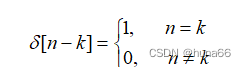 
（1.2）
单位冲激序列是数字信号处理中最重要和最基本的信号，按照信号分解的观点，我们可以说，任意离散时间信号都可以表示成移位加权的单位冲激序列之和（Any discrete-time sequence can be expressed as a sum of weighted and time shifted unit sample sequences）。
单位阶跃序列（Unit Step Sequence）
单位阶跃序列定义为
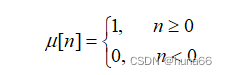（1.3）
移位的单位阶跃序列
（1.4）
单位冲激序列与单位阶跃序列有如下关系：
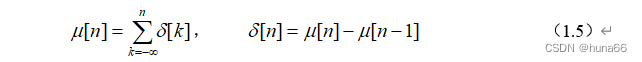， （1.5）
正弦和指数序列（Sinusoidal and Exponential Sequences）
正弦序列的一般形式为
（1.6）
式中，A，ω0和Φ均为实数，分别叫做振幅（Amplitude），角频率（Angular frequency）和相位（Phase）。
指数序列的一般形式为
（1.7）
若A，α均为实数，则x[n]为实指数序列。若令
，
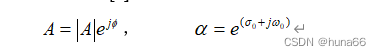则复指数序列可表示为
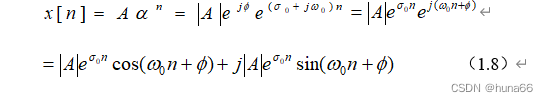（1.8）
2.2离散时间信号的MATLAB仿真
在《信号与系统实验》中，我们已经学习过如何用MATLAB来仿真信号。这里，给出若干个范例程序，目的是回顾用MATLAB仿真信号的编程方法。
程序Program1_1是用MATLAB对一个正弦信号进行仿真的程序，请仔细阅读该程序，并在计算机上运行，观察所得图形。
% Program1_1
% This program is used to generate a discrete-time sinusoidal signal and draw its plot
clear, % Clear all variables
close all, % Close all figure windows
n = -20: 20; % Specify the interval of time
w0 = 0.2*pi; % Specify the angular frequency
x = sin(w0*n); % Generate the signal
stem(n,x,'k.') % Open a figure window and plot x[n]
title('Sinusoidal signal x[n]')
xlabel('Time Index n')
执行Program1_1所得到的信号的波形图如图1.2所示。
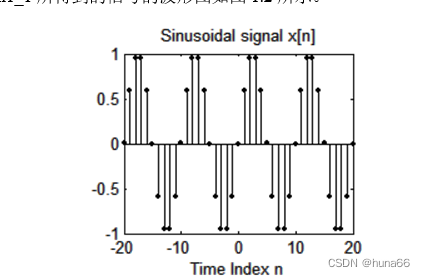
图1.2 正弦序列的时域波形
对于正弦信号，有一个有趣的现象，那就是，信号振荡剧烈程度并不总是随着ω0的增加而增加，而是当ω0等于π时，再增大ω0，信号振荡的剧烈程度反而减弱。
范例程序Program1_2绘制了不同角频率时的正弦信号的波形。程序Program1_2如下
% Program1_2
clear,close all,
n = -20: 20;
w0 = 0*pi; w1 = 0.1*pi; w2 = 0.2*pi; w3 = 0.8*pi; w4 = 0.9*pi; w5 = 1*pi;
w6 = 1.1*pi; w7 = 1.2*pi;
x0 = cos(w0*n); x1 = cos(w1*n); x2 = cos(w2*n); x3 = cos(w3*n); x4 = cos(w4*n);
x5 = cos(w5*n); x6 = cos(w6*n); x7 = cos(w7*n);
subplot(421), stem(n,x0,'k.') ,ylabel('w0=0')
subplot(422), stem(n,x1,'k.') ,ylabel('w0=0.1*pi')
subplot(423), stem(n,x2,'k.') ,ylabel('w0=0.2*pi')
subplot(424), stem(n,x3,'k.') ,ylabel('w0=0.8*pi')
subplot(425), stem(n,x4,'k.') ,ylabel('w0=0.9*pi')
subplot(426), stem(n,x5,'k.') ,ylabel('w0=1*pi')
subplot(427), stem(n,x6,'k.') ,ylabel('w0=1.1*pi')
subplot(428), stem(n,x7,'k.') ,ylabel('w0=1.2*pi')
图1.3所示波形是执行范例程序Program1_2得到的。从图中可以很清楚地看出这一点。这意味着，正弦信号的最高角频率等于π。
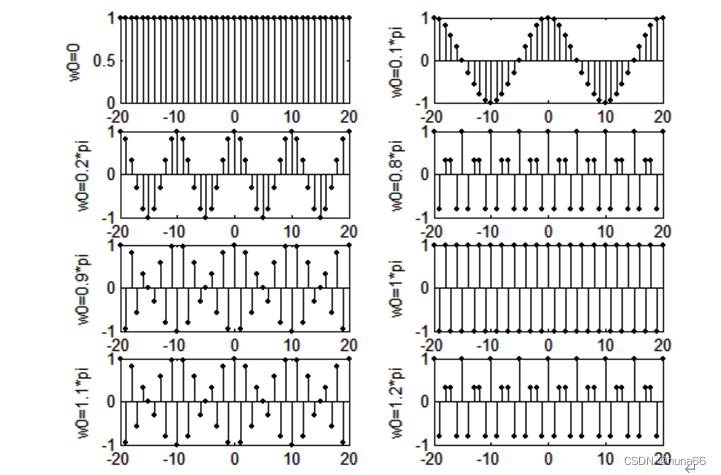
图1.3 不同频率时的正弦序列的波形
程序Program1_3用来仿真下面形式的离散时间信号：
x[n]={...., 0.1, 1.1, -1.2, 0, 1.3, ….}
↑n=0
% Program1_3
% This program is used to generate a discrete-time sequence
% and draw its plot
clear, % Clear all variables
close all, % Close all figure windows
n = -5:5; % Specify the interval of time, the number of points of n is 11.
x = [0, 0, 0, 0, 0.1, 1.1, -1.2, 0, 1.3, 0, 0]; % Generate the signal
stem(n,x,'.') % Open a figure window and draw the plot of x[n]
grid on,
title ('A discrete-time sequence x[n]')
xlabel ('Time index n')
由于在程序的stem(n,x,'.') 语句中加有'.'选项，因此绘制的图形中每根棒条线的顶端是一个实心点。
如果需要在序列的前后补较多的零的话，可以利用函数zeros()，其语法为：
zeros(1, N)：圆括号中的1和N表示该函数将产生一个一行N列的矩阵，矩阵中的所有元素均为零。利用这个矩阵与序列x[n]进行组合，从而得到一个长度与n相等的向量。
例如，当 x[n]={ 0.1, 1.1, -1.2, 0, 1.3} 时，为了得到程序Program1_3中的序列，
↑n=0
可以用这个MATLAB语句x = [zeros(1,4) x zeros(1, 2)] 来实现。用这种方法编写的程序如下：
% Program1_4
% This program is used to generate a discrete-time sinusoidal signal
% and draw its plot
clear, % Clear all variables
close all, % Close all figure windows
n = -5:5; % Specify the interval of time
x = [zeros(1,4), 0.1, 1.1, -1.2, 0, 1.3, zeros(1,2)]; % Generate the sequence
stem (n,x,'.') % Open a figure window and draw the plot of x[n]
grid on,
title ('A discrete-time sequence x[n]')
xlabel ('Time index n')
在实验中，经常要使用单位冲激序列δ[n]和单位阶跃序列μ[n]。由于MATLAB无法不支持拉丁文和西腊文，所以，我们仍用u[n]来表示单位阶跃序列。为了能够象教材中那样使用u[n]，请将下面的MATLAB函数拷贝到work文件夹中保存：
% Unit step function
function y = u(t)
y = (t>=0); % y = 1 for t > 0, else y = 0
再利用单位冲激序列δ[n]与单位阶跃序列u[n]之间的关系，就能够用单位阶跃序列u[n]表示单位冲激序列δ[n]。
离散时间单位阶跃信号u[n]除了可以直接用这个扩展函数来产生，还可以利用MATLAB内部函数ones(1,N) 来实现。这个函数类似于zeros(1,N)，所不同的是它产生的矩阵的所有元素都为1。
值得注意的是，利用ones(1,N) 来实现的单位阶跃序列并不是真正的单位阶跃序列，而是一个长度为N单位门(Gate)序列，也就是u[n]-u[n-N]。但是在一个有限的图形窗口中，我们看到的还是一个单位阶跃序列。
3.离散时间LTI系统的时域描述
3.1线性时不变系统
在分析LTI系统时，有关LTI系统的两个重要的性质是必须首先掌握和理解的。这就是线性性（Linearity）和时不变性（Time-invariance）。所谓线性性就是指系统同时满足齐次性和叠加性。这可以用下面的方法来描述。
假设系统在输入信号x1[n]作用时的响应信号为y1[n]，在输入信号x2[n]作用时的响应信号为y2[n]，给定两个常数a和b，如果当输入信号为x(t)时系统的响应信号为y(t)，且满足
x[n] = x1[n] + x2[n] 1.9(a)
y[n] = y1[n] + y2[n] 1.9(b)
则该系统具有叠加性（Additivity）。如果满足
x[n] = ax1[n] 1.10(a)
y[n] = ay1[n] 1.10(b)
则该系统具有齐次性（Homogeneity）。一个系统如果是线性系统的话，那么这个系统必须同时具有叠加性和齐次性。
又假设系统在输入信号x(t)作用时的响应信号为y(t)，对一个给定时间常数t0，如果当输入信号为x[n-n0]时，系统的响应信号为y[n-n0]的话，则该系统具有时不变性。同时具有线性性和时不变性的系统，叫做线性时不变系统，简称LTI系统。
3.2离散时间LTI系统的单位冲激响应和卷积模型
给定一个离散时间LTI系统，在系统的初始条件为零时，用单位冲激信号δ[n]作用于系统，此时系统的响应称为系统的单位冲激响应（Unit impulse response），一般用h[n]来表示。需要强调的是，系统的单位冲激响应是在激励信号为δ[n]时的零状态响应（Zero-state response）。
系统的单位冲激响应是一个非常重要的概念，对于一个系统，如果我们知道了该系统的单位冲激响应，那么，该系统对任意输入信号的响应信号都可以求得。也就是说，系统的输入信号x[n]和输出信号y[n]之间的关系可以用一个数学表达式来描述，这个数学表达式为
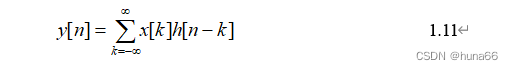
这个表达式就是LTI系统的卷积模型，它是根据系统的线性性和时不变性以及信号可以分解成单位冲激函数经推理得到的。这个表达式实际上告诉了我们一个重要的结论，那就是，任意LTI系统可以完全由它的单位冲激响应h[n]来确定（Any discrete-time LTI system can be completely specified by its unit impulse response）。由于系统的单位冲激响应是零状态响应，故按照式1.11求得的系统响应也是零状态响应。式1.11中的求和运算叫做卷积和，是描述离散时间LTI系统输入输出关系的一个重要表达式。
3.3卷积的计算
卷积的计算通常可按下面的五个步骤进行：
- 改换两个信号波形图中的横坐标，由n改为k，k变成函数的自变量；
- 把其中一个信号反褶，如把h[k]变成h[-k]；
- 把反褶后的信号做移位，移位量是n，这样n是一个参变量。在k坐标系中，n > 0时图形右移，n < 0时图形左移；
- 计算两个信号重叠部分的乘积x[k]h[n-k]；
- 完成相乘后图形的求和。
对于两个时限信号（Time-limited signal），按照上述的五个步骤，作卷积和运算时，关键是正确确定不同情况下的求和区间。只要正确地确定了求和区间，一般都能得到正确定卷积结果。尽管如此，在时域中计算卷积积分，总体上来说是一项比较困难的工作。
程序Dcovdemo用来演示上述作卷积和运算的五个步骤。本程序较为复杂，不建议读者读懂该程序，只需执行这个程序，观看程序执行过程中有关卷积积分的运算过程，以便于理解这五个步骤。
借助MATLAB的内部函数conv()可以很容易地完成两个信号的卷积和运算。其语法为：
y = conv(x,h)
其中x和h分别是两个作卷积运算的信号，y为卷积结果。
在有些时候，做卷积和运算的两个序列中，可能有一个序列或者两个序列都非常长，甚至是无限长，MATLAB处理这样的序列时，总是把它看作是一个有限长序列，具体长度由编程者确定。实际上，在信号与系统分析中所遇到的无限长序列，通常都是满足绝对可和（Absolutely summable）条件的信号。因此，可以对信号进行截断处理。对信号采取这种截短处理尽管存在误差，但是通过选择合理的信号长度，这种误差是能够减小到可以接受的程度的。若这样的一个无限长序列可以用一个数学表达式表示的话，那么，它的长度可以由编程者通过指定时间变量n的范围来确定。
例如，对于一个单边实指数序列x[n] = 0.5nu[n]，通过指定n的范围为0 ≤n ≤ 100，则对应的x[n]的长度为101点，虽然指定更宽的n的范围，x[n]将与实际情况更相符合，但是，应该注意到，当n大于某一数时，x[n]之值已经非常接近于0了。对于序列x[n] = 0.5nu[n]，当n = 7时，x[7] = 0.0078，这已经是非常小了。所以，对于这个单边实指数序列，指定更长的n的范围是没有必要的。当然，不同的无限长序列具有不同的特殊性，在指定n的范围时，只要能够反映序列的主要特征就可以了。
3.4 用线性常系数差分方程描述LTI系统
线性常系数差分方程是描述离散时间LTI系统的另一个时域模型，即系统的输入信号x[n]输出信号y[n]关系可以用下面的差分方程来表达
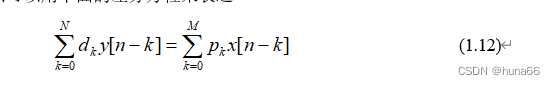(1.12)
式1.12中，max (N, M)定义为系统的阶(Order)。式1.12描述了LTI系统输入信号和输出信号的一种隐性关系（Implicit relationship）。为了求得系统响应信号的显式表达式（Explicit expression），必须对差分方程求解。
在MATLAB中，是用差分方程的系数来描述这个离散时间LTI系统的。例如，一个LTI离散时间系统的差分方程为
y[n]+y[n-1]-6y[n-2]=x[n]
MATLAB则用两个系数向量num = [1]和den = [1 1 -6]来描述该系统，其中num和den分别表示系统差分方程右边和左边的系数，按照差分运算的递减排列。
在用num和den定义了一个离散时间LTI系统之后，可以利用MATLAB来求解系统响应。求解离散时间系统的响应的一个非常有用的MATLAB函数就是filter()。它可以用来求解系统的在输入信号x[n]作用下的零状态响应（Zero-State Response），也可以求解系统在这个输入信号作用下的完全响应（Complete Solution）。其用法描述如下：
y = filter(num, den, x)，求系统在输入x作用下的零状态响应y，x与y的长度相同。
y = filter(num, den, x, ic)，求系统在输入x作用下的完全响应y，x与y的长度相同。其中ic为系统的初始条件（Initial Condition），即ic = [y[-1], y[-2], y[-3], ......, y[-N]]。
例题1.1 给定一个离散时间LTI系统，它的差分方程为
y[n]+0.1y[n-1]-0.06y[n-2]=x[n]
若输入信号为x[n] = 0.5nu[n]，系统的初始条件为ic = [0, 1]，编写程序，绘制输入信号x[n]、系统的零状态响应yzs[n]和系统的完全响应信号y [n]的波形图。
MATLAB范例程序如下：
% Program1_5
clear,close all,
num = 1; den = [1 .1 -0.06];
n = 0:20; x = 0.5.^n.*u(n); ic = [0 .9];
yzs = filter(num,den,x); y = filter(num,den,x,ic);
subplot(221)
stem(n,x,'.'), title('The input sequence x[n]'), axis([0,20,-0.5,1.5])
subplot(222)
stem(n,yzs,'.'), title('The zero-state response yzs[n]'), axis([0,20,-0.5,1.5]),
xlabel('Time index n')
subplot(223)
stem(n,y,'.'), axis([0,20,-0.5,1.5]), title('The total solution y[n]')
xlabel('Time index n')
二、实验内容
实验前，必须首先阅读本实验原理，读懂所给出的全部范例程序。实验开始时，先在计算机上运行这些范例程序，观察所得到的信号的波形图。并结合范例程序应该完成的工作，进一步分析程序中各个语句的作用，从而真正理解这些程序。
实验前，一定要针对下面的实验项目做好相应的实验准备工作，包括事先编写好相应的实验程序等事项。
Project 1：移动平均滤波器（The Moving Average Filter）
一个因果的M点移动平均FIR滤波器的差分方程为：
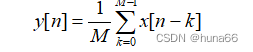(1.13)
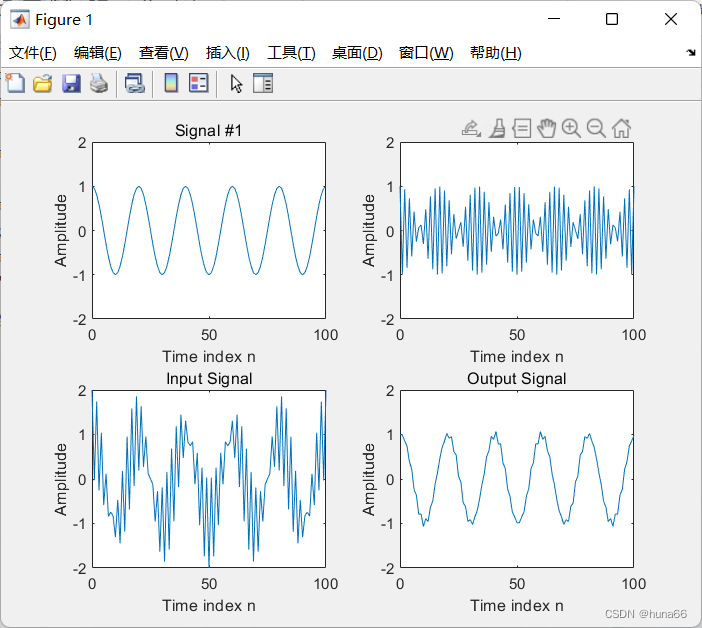
下面我们通过从若干个正弦信号之和组成的信号中滤出高频分量，来研究式(1.13)表示的该移动平均滤波器的使用。实验用程序如下
% Program P1_1
% Simulation of an M-point Moving Average Filter
% Generate the input signal
clear, close all,
n = 0:100;
s1 = cos(2*pi*0.05*n); % A low-frequency sinusoid
s2 = cos(2*pi*0.47*n); % A high frequency sinusoid
x = s1+s2;
% Implementation of the moving average filter
M = input('Desired length of the filter = ');
num = ones(1,M);
y = filter(num,1,x)/M;
% Display the input and output signals
subplot(2,2,1); plot(n, s1); axis([0, 100, -2, 2]); xlabel('Time index n'); ylabel('Amplitude');
title('Signal #1');
subplot(2,2,2); plot(n, s2); axis([0, 100, -2, 2]); xlabel('Time index n'); ylabel('Amplitude');
title('Signal #2');
subplot(2,2,3); plot(n, x); axis([0, 100, -2, 2]); xlabel('Time index n'); ylabel('Amplitude');
title('Input Signal');
subplot(2,2,4); plot(n, y); axis([0, 100, -2, 2]); xlabel('Time index n'); ylabel('Amplitude');
title('Output Signal');
