目录
本文是介绍基4 SRT算法前的第五篇补充文章《On the fly conversion》。
一、On-the-Fly Conversion
冗余数集表示的商集可以加快除法中商选择的递归速度,由于商由有符号的冗余数集组成,在迭代完成后需要将一连串的商数结果转换至二进制补码格式。比如基4的某个商商集为{-2,-1,0,1,2},迭代2次得到商值为{2,-1},其实际表示的数为2*4-1=7,所以,如何得到这个值呢?
传统的方法即使用进位加法器实现,或者使用快速的树形加法器,但是转换的延迟依然与加法器的位宽取2的对数成正比,所以在除法中需要额外的周期,增加了除法操作的延迟。
然而,根据QDS函数输出得到转换的结果并不是不可能。所以,应运而生的On-the-Fly Conversion算法可用来避免额外的计算周期,On-the-Fly Conversion算法中文名称翻译为“飞速转换算法”比较多见。飞速转换算法用于SRT算法中的每一个产生的商数,每次迭代产生一个商数,最高位商数最先产生,在整个迭代过程中,Q[j+1]和Q[j+1] – ulp同时产生,并且分别保存至2个寄存器A和B中,第j次迭代结果表示为A[j+1]和B[j+1]。Q[j+1]表示了在选择了QDS函数后二进制格式下的商值。
A和B寄存器以如下迭代公式更新:
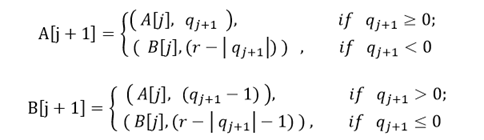
上式中A[0]=B[0]=0,括号表示级联,没有进位和借位的操作,每产生一个商数会更新以上寄存器,当最后一个商值输出被用于更新时,商值的二进制补码格式可从A寄存器中读出。
其本质为A和B寄存器预先存储根据商集得到的值,方法比较巧妙,不需要加减法。
以基2商数集为例,商集为{-1,0,1},r=2,得到的商数P=0.1101-100-11010,将其转换为二进制补码格式,过程如下:
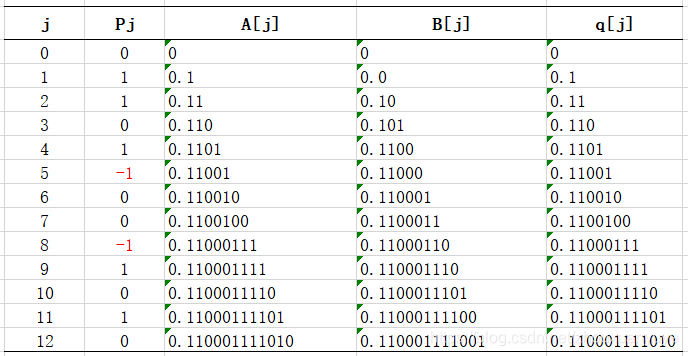
论文:On-the-Fly Conversion of Redundant into Conventional Representations.
二、Verilog设计
设计一个基4 SRT的on-the-fly conversion模块,商数集为{-2,-1,0,1,2}。
首先用3bit表示以上商数集:
q=010,表示2
q=001,表示1
q=000,表示0
q=111,表示-1
q=110,表示-2
定义A,B寄存器,以及更新的线型A_next和B_next。
更新公式如上节所示,即:

此处r=4,级联项q, r-|q|,q-1,r-1-|q|每项都是2比特。其中的有加减法的部分可以通过q值真值表化简,不需要加法器。

例子,商数集为{2,-1,-2,-2,-2}。
预期的商应为:2*4^4 + (-1)*4^3 + (-2)*4^2 + (-2)*4^1 + (-2)*4^0=406
仿真结果为:406
结果一致。

源码参考公众号回复“01a”,谢谢您的阅读!
原创不易,如果对您有帮助,记得点赞关注哦。欢迎批评指正,谢谢鼓励!
一起“纸上谈芯”,共同学习:
