多类别分类——逻辑回归和神经网络

一、逻辑回归应用于多类别分类
假设有一个训练集如下图左部分所示，有3个类别。逻辑回归的方法是将其分成3个二元分类问题。先从类别1开始，创建一个新的“伪”训练集，类别2和类别3定为负类，类别1设定为正类，如图所示：

对新的训练集训练一个标准的逻辑回归分类器，记作$h_{\theta }^{\left(1\right)}\left(x\right)$。接着类似地，选择另一个类标记为正向类，将其它类都标记为负向类，将这个模型记作$h_{\theta }^{\left(2\right)}\left(x\right)$。依此类推，得到一系列的模型为：$$h_{\theta }^{\left(i\right)}\left(x\right)=p\left(y=i|x;\theta \right)\left(i=1,2,3,...,k\right)$$
最后，在做预测时将所有的分类模型都运行一遍，对每一个输入变量，都选择最高可能性的输出变量。也就是输入x，选择一个让$h_{\theta }^{\left(i\right)}\left(x\right)$最大的i。
二、神经网络
神经网络是一组神经元连接在一起的集合，每一个神经元是一个学习模型。神经元（也叫激活单元，activation unit）采纳一些特征作为输入，并且根据本身的模型提供一个输出。神经网络模型中每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络，第一层为输入层，最后一层为输出层，中间一层为隐藏层。为每一层都增加一个偏差单位（bias unit）即常数项。

模型描述：$a_i^{\left(j\right)}$代表第j层的第i个激活单元，${\theta }^{\left(j\right)}$代表从第j层映射到第j+1层时的权重的矩阵，其尺寸为：以第j+1层的激活单元数量为行数，以第j层的激活单元数加一为列数。如上图所示的神经网络中${\theta }^{\left(1\right)}$的尺寸为3*4。对于上图所示的模型，激活单元和输出分别表达为：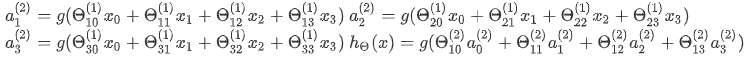

每一个a都是由上一层所有的x和每一个x所对应的θ决定的，这样从左到右的算法称为前向传播算法。利用向量化的方法表示模型，以上图三层神经网络的第二层计算为例：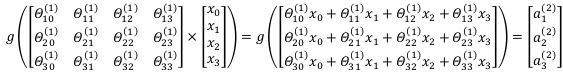

令$z^{\left(2\right)}={\theta }^{\left(1\right)}x$，则$a^{\left(2\right)}=g\left(z^{\left(2\right)}\right)$，计算后添加$a_0^{\left(2\right)}=1$。计算输出的值为：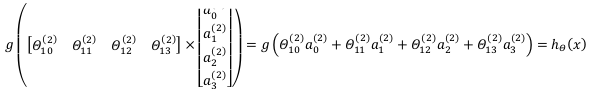

三、以吴恩达机器学习课程练习材料实现，分别使用逻辑回归和神经网络进行多类别分类。背景是识别手写数字，代码实现来源参考：吴恩达机器学习作业Python实现(三)：多类分类和前馈神经网络
原始训练数据集以matlab的数据存储格式.mat保存，数据中有5000个训练样本，其中每个训练样本是一个20像素×20像素灰度图像的数字，每个像素由一个浮点数表示，该浮点数表示该位置的灰度强度。每个20×20像素的网格被展开成一个400维的向量，得到一个5000×400矩阵X，每一行作为一个训练样本。训练集的第二部分是表示训练集标签的5000维向量y，“0”标记为“10”，而“1”到“9”按自然顺序标记为“1”到“9”。
数据加载及可视化的代码如下：

from scipy.io import loadmat
import numpy as np
import matplotlib.pyplot as plt

data=loadmat('ex3data1.mat')    #读取matlab格式的数据集
#print(data.keys()) #查看变量名
#print(np.unique(y))    #查看有几类标签
X=data['X'] #获得特征数据
y=data['y'] #获得类别数据

#随机画25个数字
def plot_25_image(X):
    sample_idx=np.random.choice(np.arange(X.shape[0]),25)    #随机选取25个样本
    sample_images=X[sample_idx,:]   #获得随机抽取的样本特征
    fig,ax_array=plt.subplots(nrows=5,ncols=5,sharey=True,sharex=True,figsize=(8,8))    #把父图分成5*5个子图，设置图的大小，True设置x和y轴属性在所有子图中共享
    for row in range(5):
        for column in range(5):
            ax_array[row,column].matshow(sample_images[5*row+column].reshape((20,20)),cmap='gray_r')    #绘制数字图像,cmap设置绘制风格为白底黑字
    plt.xticks([])  #去除刻度，保证美观
    plt.yticks([])
    plt.show()
plot_25_image(X)

随机打印25个数字如下图所示：

使用逻辑回归进行多类别分类代码如下：

#定义Sigmoid函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

#定义正则化后的代价函数
def regularized_cost(theta,X,y,a):
    thetaReg=theta[1:]  #不惩罚第一项θ0
    first=-y*np.log(sigmoid(X@theta))+(y-1)*np.log(1-sigmoid(X@theta))  #原先代价函数
    reg=a*(thetaReg@thetaReg)/(2*len(X))    #正则化项
    return np.mean(first)+reg

#定义正则化后的梯度
def regularized_gradient(theta,X,y,a):
    reg = 1 / len(X) * theta
    reg[0] = 0  #不惩罚第一项θ0
    first=1/len(X)*X.T@(sigmoid(X@theta)-y) #原先梯度
    return first+reg

#使用高级优化算法训练10个分类器
from scipy.optimize import minimize
def one_vs_all(X,y,l,K):    #参数l是正则化参数，K是类别数量
    all_theta=np.zeros((K,X.shape[1]))  #初始化参数，行数等于类别数量，列数等于特征数量
    for i in range(1,K+1):
        theta=np.zeros(X.shape[1])  #初始化每个分类器的参数
        y_i=np.array([1 if label==i else 0 for label in y]) #将y从类标签转换为每个分类器的二进制值（要么是类i，要么不是类i）
        ret=minimize(fun=regularized_cost,x0=theta,args=(X,y_i,l),method='BFGS',jac=regularized_gradient,options={'disp':True}) #使用minimize，fun是优化的目标函数，x0定义初值，args元组是传递给优化函数的参数，method是求解的算法，jac提供梯度函数，disp设置true输出收敛信息
        all_theta[i-1,:]=ret.x  #保存每个分类器的最终参数
    return all_theta

#计算预测类别
def predict_all(X,all_theta):
    h=sigmoid(X@all_theta.T)    #计算获得每个样本分别对应10个类别的概率
    h_argmax=np.argmax(h,axis=1)    #按行方向搜索每个样本所属类别概率最大对应的索引
    h_argmax=h_argmax+1 #索引加1得到分类器最终预测出来的类别
    return h_argmax

#处理数据并训练分类器
X=np.insert(X,0,1,axis=1)   #特征集前面添加一列1，以便计算截距项
y=y.flatten()   #类别数据消除列的维度，方便后面的计算
all_theta=one_vs_all(X,y,1,10)  #获得每个分类器的参数
y_pred=predict_all(X,all_theta) #预测类别
accuracy=np.mean(y_pred==y) #计算预测准确率
print('accuracy={0}%'.format(accuracy*100))

使用神经网络进行多类别分类代码如下：

#定义Sigmoid函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

#处理数据
data = loadmat('ex3weights.mat')    #读取已经训练好的权重
#print(data.keys())
theta1 = data['Theta1'] #获得隐藏层参数
theta2 = data['Theta2'] #获得输出层参数
#print(theta1.shape,theta2.shape)
data = loadmat('multi_class_cl.mat')
X = data['X']  #获得特征数据
y = data['y']
y = y.flatten()	#类别数据消除列的维度，方便后面的计算
X = np.insert(X, 0, 1, axis=1)	#特征集前面添加一列1，以便计算截距项
print(X.shape,y.shape)

#训练模型
a1 = X  #输入层为特征集
z2 = a1 @ theta1.T  #计算隐藏层输入数据
z2 = np.insert(z2, 0, 1, axis=1)    #数据集前面添加一列1，以便计算截距项
a2 = sigmoid(z2)    #计算隐藏层输出数据
z3 = a2 @ theta2.T  #计算输出层输入数据
a3 = sigmoid(z3)    #计算输出层输出数据

y_pred = np.argmax(a3, axis=1) + 1	#获得每个样本所属类别概率最大的作为最终预测出来的类别
accuracy = np.mean(y_pred == y)	#计算预测准确率
print('accuracy={0}%'.format(accuracy * 100))

运行代码分别获得两种方法的预测准确率，逻辑回归模型的准确率为94.48%，神经网络的准确率为97.52%，可以看出神经网络的准确性要高于逻辑回归模型。

（结语个人日记：最近开心的事情大概是持续将近一年时间的大创被评为优秀了叭，虽然做出来的结果自己和队友都没有完全满意，但是付出的过程是问心无愧的。为了解决问题思考各种可能的方法，边查边写代码，一有空闲时间就跑代码，每周固定和老师例会讨论，尝试实践了很多思路。也算终于画上句号了，还有留下曾经自己充实努力的回忆。）