求第k小元素问题

k小元素问题是利用分治法进行求解的经典问题之一。

问题描述

已知一个长度为n的数组，返回数组中的第k小的元素。
有些问题中求解的是第k大元素，方法类似。

分析设计

要想找出第k小的元素，我们首先想到的方法肯定是先将数组进行排序，返回第k个元素即可，然而利用排序的方法求解时间复杂度至少为O(nlogn)，是否存在一种算法使得时间复杂度为O(n)？

分治法

当数组长度，即问题规模很大时，分治法是一种很好的算法解决该问题。当问题规模达到一定的阈值时，分治法就具有较高的效率。在求第k小元素中，该阈值为44，即数组长度超过44时，采用分治法会获得较高小效率。
（在实际编程测试中，由于测试数据较小，我采用的阈值为5。）

利用分治法求解的基本思路为：

1. 当问题规模小于阈值时，直接采用排序算法返回结果。（我使用的是归并排序。）
2. 当问题规模大于阈值时，我们将n个元素以5个一组，划分为n/5组（剩余元素一组，不会有影响），分别排序找出中位数，将所有中位数放入一个数组中，重复第2步，最终得到整个数组的中位数m。（其中的数学原理不再赘述。）
3. 将整个数组分为3个部分：a₁，a₂，a₃，分别代表小于、等于、大于m的元素。
4. 存在三种情况：
   (1). 若a₁的元素个数大于等于k，则第k小元素在 a₁中，在a₁中递归查找第k小元素；
   (2). 若a₁、a₂的元素个数之和大于等于k，则中位数m即为第k小元素，返回m；
   (3). 否则，第k小元素在a₃中，在a₃中递归查找第(k - (a₁.length + a₂.length))小元素。

源代码

#include <iostream>
#include <vector>
using namespace std;

//归并排序
void merge(int a[], int start1, int end1, int start2, int end2) {
	int i = start1, j = start2;
	int n = (end1 - start1 + 1) + (end2 - start2 + 1);
	vector<int> temp(n);
	int k = 0;
	while (i <= end1 && j <= end2) {
		if (a[i] < a[j])
			temp[k++] = a[i++];
		else
			temp[k++] = a[j++];
	}
	while (i <= end1)
		temp[k++] = a[i++];
	while (j <= end2)
		temp[k++] = a[j++];
	for (int i = 0; i < n; i++)
		a[start1 + i] = temp[i];
}

void MergeSort(int a[], int start, int end) {
	if (start < end) {
		int mid = (start + end) >> 1;
		MergeSort(a, start, mid);
		MergeSort(a, mid + 1, end);
		merge(a, start, mid, mid + 1, end);
	}
}

int select(int a[], int start, int end, int k) {
	int n = end - start;
	if (n < 5) {
		MergeSort(a, start, end - 1);
		return a[start + k - 1];
	}

	int s = n / 5;
	int *m = new int[s];	//中位数数组
	int i;
	for (i = 0; i < s; i++) {
		MergeSort(a, start + i * 5, start + i * 5 + 5 - 1);
		m[i] = a[start + i * 5 + 2];
	}
	//int mid = select(a, 0, s - 1, (s - 1) / 2);  //中位数数组中位数
	MergeSort(m, 0, i - 1);
	int mid = m[i / 2];
	int *a1 = new int[n];
	int *a2 = new int[n];
	int *a3 = new int[n];
	int num1 = 0, num2 = 0, num3 = 0;
	for (int i = start; i < end; i++) {
		if (a[i] < mid)
			a1[num1++] = a[i];
		else if (a[i] == mid)
			a2[num2++] = a[i];
		else
			a3[num3++] = a[i];
	}
	if (num1 >= k)
		return select(a1, 0, num1, k);
	if (num1 + num2 >= k)
		return mid;
	else
		return select(a3, 0, num3, k - num1 - num2);
}

int main() { 
	int n;
	cout << "输入数组个数：";
	cin >> n;
	int *a = new int[n];
	cout << "输入数组元素：";
	for (int i = 0; i < n; i++) 
		cin >> a[i];
	int k;
	cout << "输入所求第几小元素k：";
	cin >> k;
	cout << "第" << k << "小元素为：" << select(a, 0, n, k) << endl;

	delete[] a;
	system("pause");
	return 0;
}

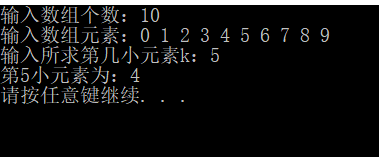
运行结果