YOLO系列:YOLO V3模型讲解
- 论文标题:YOLO V3:An Incremental Improvement (CVPR 2018)
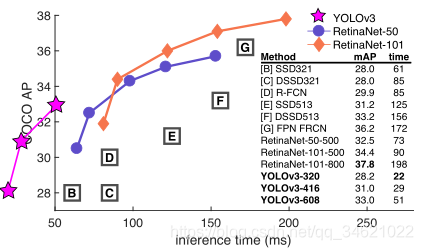
- 效果(COCO 数据集):
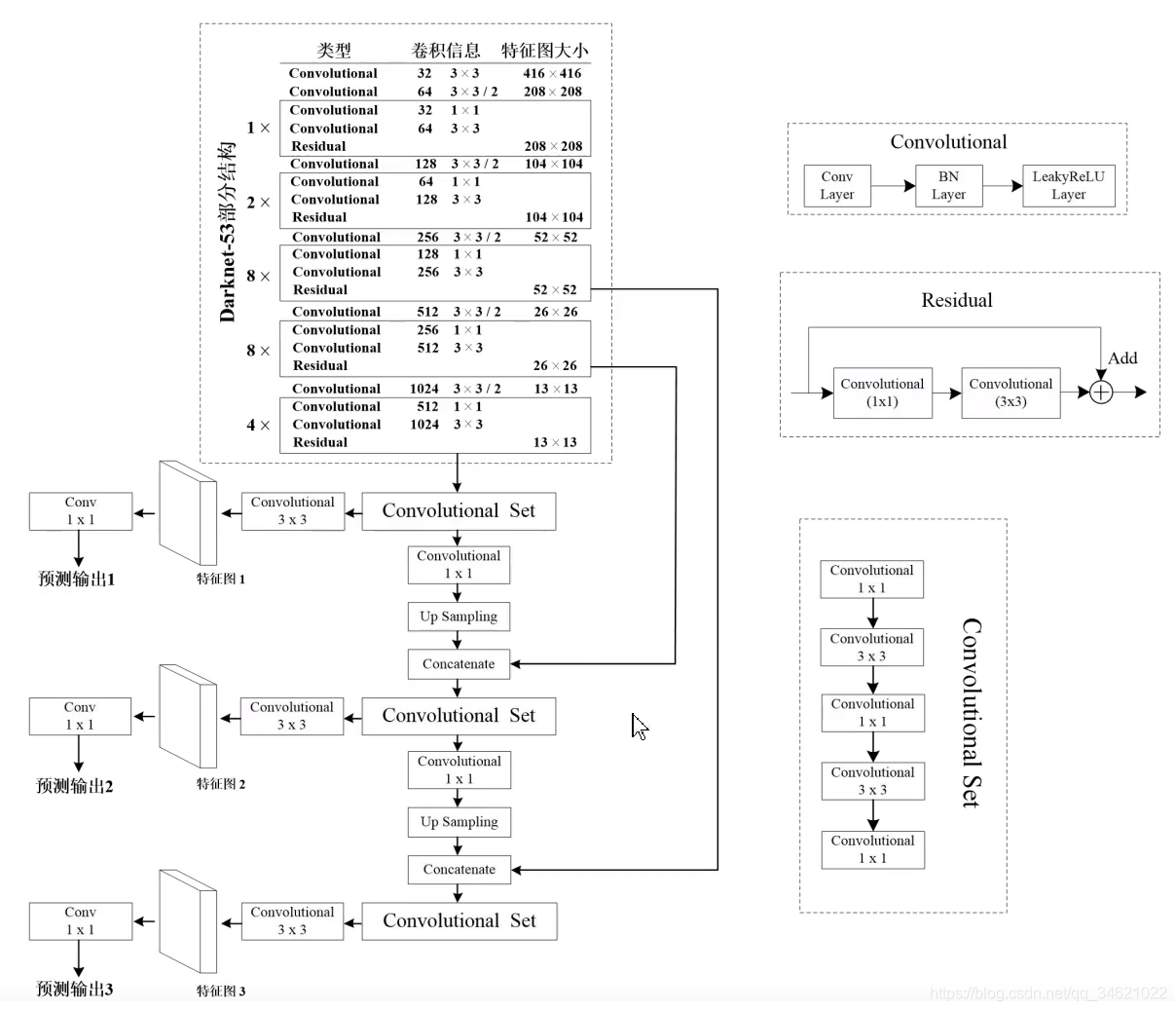
- 模型结构:(DarkNet-53有53个卷积层)
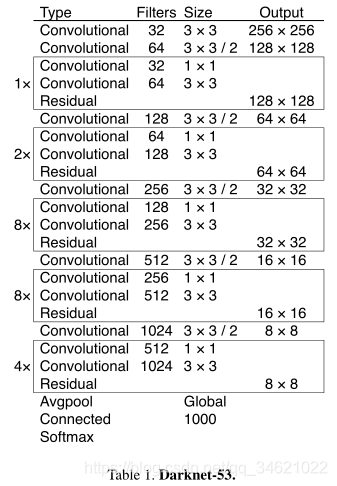
使用卷积层代替了最大池化下采样层,DarkNet-53卷积核的个数比ResNet也少很多。
效果对比: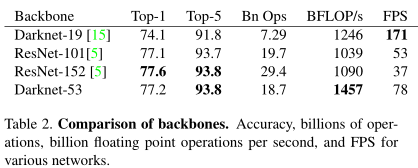
DarkNet 53检测效果和ResNet152基本持平,但检测速度慢了两倍。
- 使用K-means 聚类算法得到了先验框的尺度,文章选择了9个聚类,3个尺度,也就是在每个预测特征图上会预测三种尺度的先验框。每个预测特征图上会有N × N × [ 3 ∗ ( 4 + 1 + 80 ) ] N \times N \times [3 * (4+1+80)]N×N×[3∗(4+1+80)] (N表示特征图大小,80表示COCO数据集中的80个类别的分数信息,4表示坐标(t x t_xtx,t y t_yty,t w t_wtw,t h t_hth), 1表示置信度。)
| 特征图层 | 特征图大小 | 预设边界框尺寸 | 预设边界框数量 |
|---|---|---|---|
| 特征图层1 | 13 × \times× 13 | (116 × \times× 90);(156 × \times× 198);(373 × \times× 326) | 13 × \times× 13 × \times× 3 |
| 特征图层2 | 26 × \times× 26 | (30 × \times× 61);(62 × \times× 45);(59 × \times× 119) | 26 × \times× 26 × \times× 3 |
| 特征图层3 | 52 × \times× 52 | (10 × \times× 13);(16 × \times× 30);(33 × \times× 23) | 52 × \times× 52 × \times× 3 |
- Bounding box计算:
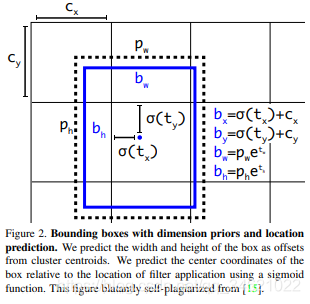
- 正负样本匹配:每个groundtruth 都分配一个bounding box prior,分配原则-将与gt重合最大的作为正样本,如果不是最大但是大于某个值,则丢弃这些预测框(文章设置阈值为0.5),剩下的样本为负样本。如果一个bounding box prior不是正样本那么就不再计算它的定位 损失和类别损失,仅计算confidence score。
- 损失计算:(置信度损失+分类损失+定位损失)
L ( o , c , O , C , l , g ) = λ 1 L c o n f ( o , c ) + λ 2 L c l a ( O , C ) + λ 3 L l o c ( l , g ) L(o,c,O,C,l,g) = \lambda_1L_{conf}(o,c) + \lambda_2L_{cla}(O,C) + \lambda_3L_{loc}(l,g)L(o,c,O,C,l,g)=λ1Lconf(o,c)+λ2Lcla(O,C)+λ3Lloc(l,g)
λ 1 \lambda_1λ1, λ 2 \lambda_2λ2,λ 3 \lambda_3λ3为平衡系数。
置信度损失:
L c o n f ( o , c ) = ∑ i ( o i l n ( c i ^ ) + ( 1 − o i ) l n ( 1 − c i ^ ) ) N L_{conf}(o,c) = \frac{\sum_{i}(o_iln(\hat{c_i})+(1-o_i)ln(1-\hat{c_i}))}{N}Lconf(o,c)=N∑i(oiln(ci^)+(1−oi)ln(1−ci^))
c i ^ = s i g m o i d ( c i ) \hat{c_i}=sigmoid(c_i)ci^=sigmoid(ci)
其中o i ∈ [ 0 , 1 ] o_i\in[0,1]oi∈[0,1], 表示预测目标边界框与真实边界框的I O U IOUIOU,c cc为预测值,c i ^ \hat{c_i}ci^为c cc通过s i g m o i d sigmoidsigmoid函数得到的预测置信度,N为正负样本个数。
类别损失: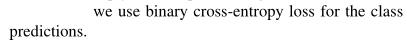
L c l a ( O , C ) = − ∑ i ∈ p o s ∑ j ∈ c l a ( O i j l n ( C i j ^ ) + ( 1 − O i j ) l n ( 1 − C i j ^ ) ) N p o s L_{cla}(O,C) = - \frac{\sum\limits_{i \in pos}\sum\limits_{j \in cla}(O_{ij}ln(\hat{C_{ij}})+(1-O_{ij})ln(1-\hat{C_{ij}}))}{N_{pos}}Lcla(O,C)=−Nposi∈pos∑j∈cla∑(Oijln(Cij^)+(1−Oij)ln(1−Cij^))
C i j ^ = S i g m o i d ( C i j ) \hat{C_{ij}} = Sigmoid(C_{ij})Cij^=Sigmoid(Cij)
其中O i j ∈ O_{ij}\inOij∈ {0,1},表示预测预测目标边界框i ii中是否存在第j jj类目标,C i j C_{ij}Cij为预测值,C i j ^ \hat{C_{ij}}Cij^为C i j C_{ij}Cij通过S i g m o i d SigmoidSigmoid函数得到的目标概率,N p o s N_{pos}Npos为正样本个数。
定位损失:
训练期间使用差值平方计算方式: