机器人坐标变换

位姿与点的描述

一个在空间中运动的物体，在选定的坐标系下，可以通过一个向量描述其位置，而物体的姿态需要一个自身的坐标系来描述。所以需要知道物体的姿态，就需要在确定物体自身坐标系后，找到自身坐标系与世界坐标系之间的关系。为什么需要知道两者之间的关系呢？因为在一个机器人中，有若干个运动结构，需要知道各个运动结构之间的关系，才可以明确操控机器人的运动，世界坐标系就是联通各个子坐标系的桥梁。

子坐标系下点在世界坐标系下的描述

1.子坐标系B相对于世界坐标系A只有平移

子坐标系B相对与世界坐标系A只有位置的变化，没有姿态的变化，在B坐标系中的点P的位置可以通过下式变换为在坐标系A下的描述：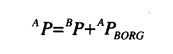

P点在图中的表示：

的各个分量可以通过下式来表示：

2.子坐标系B相对于世界坐标系A只有旋转

在求解子坐标系B相对于世界坐标系A有旋转时，需要用到旋转矩阵，旋转矩阵就是一个3*3的矩阵，其具有一下性质：
1.各列的都是单位向量
2.每列单位向量正交
以上两点性质可以说明旋转矩阵只有三个自由度，B相对于A的旋转矩阵等于A相对于B的旋转矩阵，即：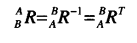

也可以表示为：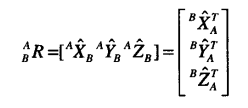

如图：

在子坐标B中有P，需要将P表示在世界坐标系A中，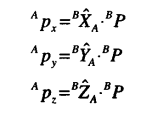

3.一般情况下的坐标变换

如图：

一般情况下的坐标系其实是以上两种变换的组合，首先将引入中间坐标系A`，使其姿态与A相同，而原点与B重合，先求出B相对于A‘的旋转矩阵R，然后求出A与A’的平移，就以可以算出P在A坐标系下的位置，算法如下：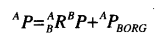

为方便，引入T矩阵，T是4*4矩阵，可以计算：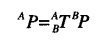

展开式为：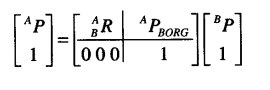

%%本文来源机器人学导论第三版