Project1
火车车厢重排调度
姓名 饶
姓名 苏
姓名 卢
姓名 彭
【题目要求】
问题描述:
一列火车要将n节车厢分别送往n个车站。车站按1~n的次序编号,火车按照n, n-1, … , 1的编号次序经过车站假设车厢的标号就是其目的地车站的编号。
题目要求:
给定一个任意的车厢排列次序。重新排列车厢,使其按照从1到n的次序排序。给出调度的详细步骤。规定重排调度时车厢只能从入轨到缓冲铁轨,或者从缓冲铁轨到出轨。如图1所示。
【数据结构与算法】
数据结构:栈
算法:接收一组由n个数组成的数据,按倒序对数据进行处理。
设置一个参照值,参照值代表下一个要过去的车厢编号。下一个过去的车厢可能在入轨队列中,也可能在缓冲铁轨中。若参照值与入轨队列队头或缓冲铁轨的顶部的车厢编号相等,则将该车厢出轨,并将参照值加一。
若车厢编号不等于参照值,则将其放进缓冲铁轨中。所有的缓冲铁轨用栈来表示,栈储存在一个vector容器中,从0开始计数。从第0条缓冲铁轨开始,遍历所有的栈顶元素,若栈顶元素大于该车厢编号,便将该车厢压栈,否则检查下一个栈。当所有栈顶都遍历过但没有符合条件的栈时,新开一个栈,将该车厢压栈(相当于现实中有多条缓冲铁轨,需要用到多少条就申请多少条)。每次参照值变化,就要对比入轨队列队头和遍历所有栈的栈顶。直到所有车厢成功出轨。
【测试数据、结果及分析】
以n = 5为例:
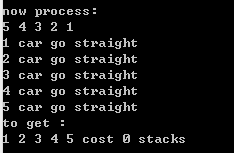
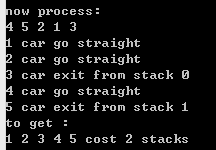
①倒序排列。输入:5 4 3 2 1;输出如图2-1所示。
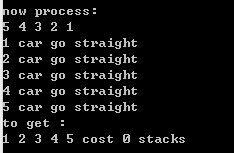
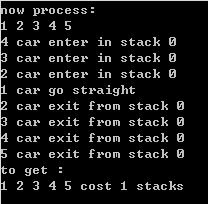
②顺序排列。输入:1 2 3 4 5;输出如图2-2所示。
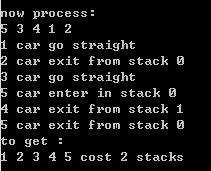
③随机排列1。输入:5 3 4 1 2;输出如图2-3所示。
④随机排列2。输入:4 5 2 1 3;输出如图2-4所示。
⑤随机排列3。输入:1 4 3 2 5;输出如图2-5所示。
以n = 10为例:
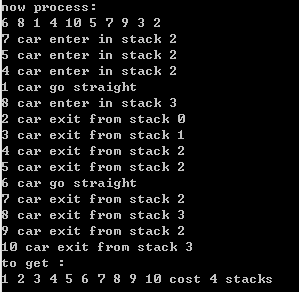
随机排列。输入:6 8 1 4 10 5 7 9 3 2;输出如图2-6所示。
以n = 100为例:
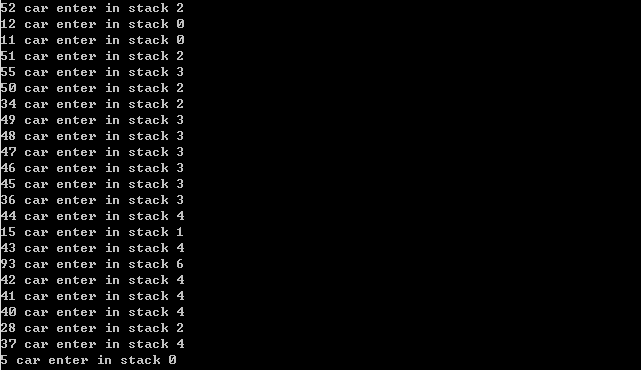
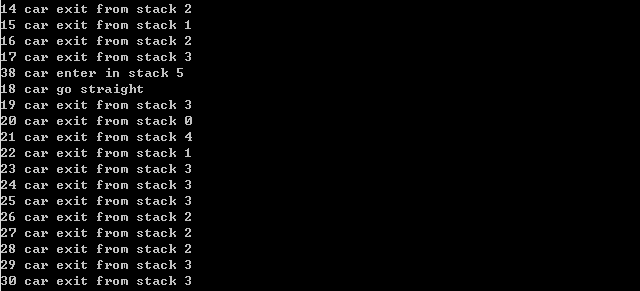
随机排列。输入:18, 38, 39, 4, 21, 6, 2, 7, 9, 10, 13, 14, 3, 17, 19, 1, 23, 24, 25,8,16, 26, 27, 68, 29, 30, 31, 81, 100, 32, 86, 33, 35, 5, 37, 28, 40, 41, 42, 93, 43, 15, 44, 36, 45, 46, 47, 48, 49, 34, 50, 55, 51, 11, 12, 52, 53, 56, 60,57, 59, 61, 62, 67, 96, 98, 99, 69, 70, 71, 72, 74, 75, 95, 76, 58, 77, 79, 73, 80, 82, 83,97, 84, 54, 85, 78, 87, 88, 22, 89, 63, 64, 65, 66, 90, 91, 92, 94, 20;输出如图2-7所示。
代码:
#include <iostream>
#include <stack>
#include <string>
#include <cstdlib>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> input, output;
void initialize() {
input.clear();
output.clear();
}
void process(int n) {
cout << "now process: " << endl;
for (int i = 0; i < input.size(); i++) {
cout << input[i] << " ";
}
cout << endl;
int count = 1;
vector< stack<int> > S;
while (1) {
while (!input.empty()) {
if (count == input.back()) {
output.push_back(count);
input.pop_back();
cout << count << " car go straight" << endl;
count++;
}
else {
break;
}
}
if (!input.empty()) {
bool isPush = false;
int a = 0;
for (; a < S.size(); a++) {
if (S[a].empty() || S[a].top() > input.back()) {
S[a].push(input.back());
isPush = true;
cout << input.back() << " car enter in stack " << a << endl;
input.pop_back();
break;
}
}
if (!isPush) { // if the stacks are not enough, push one
stack<int> add;
add.push(input.back());
S.push_back(add);
cout << input.back() << " car enter in stack " << a << endl;
input.pop_back();
}
}
for (int a = 0; a < S.size(); a++) {
while (!S[a].empty() && S[a].top() == count) {
output.push_back(count);
S[a].pop();
cout << count << " car exit from stack " << a << endl;
count++;
a = 0;
}
}
if (output.size() == n) break;
}
cout << "to get :" << endl;
for (int i = 0; i < output.size(); i++) {
cout << output[i] << " ";
}
cout << "cost " << S.size() << " stacks " << endl << endl;
}
void test1() {
int a[5] = { 1, 2, 3, 4, 5 };
do {
initialize();
for (int i = 0; i < 5; i++) {
input.push_back(a[i]);
}
process(5);
} while (next_permutation(a, a + 5));
}
void test2() {
int a[10] = { 1, 2, 3, 4, 5,
6, 7, 8, 9, 10};
do {
initialize();
for (int i = 0; i < 10; i++) {
input.push_back(a[i]);
}
process(10);
} while (next_permutation(a, a + 10));
}
int main() {
test1();
// test2();
system("pause");
return 0;
}
【项目总结】
本次项目通过对火车调度这一实际问题的分析与设计,加深了小组成员对栈的认识与了解:栈是限定仅在表头进行插入和删除操作的线性表。它按照先进后出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。
解决实际问题的算法要具有以下的特征才能有效的完成设计要求:(1)有穷性。算法在执行有限步后必须终止。(2)确定性。算法的每一个步骤必须有确切的定义。(3)可行性。满足实际问题的需求。
在算法设计的整个过程中,小组成员一共提出了两个模型。为排除极端数据对算法的影响,小组成员不断测试程序并修复算法中的不足之处。为适应实际问题的操作,小组成员不断测试程序并改进算法。
在小组实践过程中,需要发挥小组各成员的积极性和能动性,同时要发扬团队协作精神。