相关知识介绍
- 排列
我们把由1,2,3,…,n组成的一个有序数组,称为 n \ n n级排列。
例如:12和21都是2级排列,123为3级排列。
那么3145是不是一个5级排列呢?!!!3145不是5级排列。
注: n \ n n级排列中的数必须是连续的; n \ n n级排列一共有 n ! \ n! n!种。 - 逆序
在一个 n \ n n级排列中,如果较大的数排在较小的数前面,则称为逆序,记作 A \ A A。而逆序的总数称为逆序数,记作 N ( A ) \ N(A) N(A)。
例如:排列4213中,数字“4”比数字“2”大,且排在“2”前面,则该排列是一个逆序。它的逆序数记作 N \ N N(4213)=3+1+0=4。(4后面有3个数比4小,2后面有1个数比2小,1后面有0个数比1小。)
逆序数为偶数时,称为偶排列;逆序数为奇数时,称为奇排列。
特别地,对 N ( 123 … n ) = 0 \ N(123…n)=0 N(123…n)=0,称 123 … n \ 123…n 123…n为标准排列,或自然排列。
对 N ( n ( n − 1 ) … 21 ) = n − 1 + ( n − 2 ) + … + 2 + 1 = ( n − 1 ) n 2 \ N(n(n-1)…21)=n-1+(n-2)+…+2+1=\frac{(n-1)n}{2} N(n(n−1)…21)=n−1+(n−2)+…+2+1=2(n−1)n
为避免出错,数逆序数时,从第一个数开始,依次数后面有几个比它小的数,再求出累和。 - 对换
在一个 n \ n n级排列中,交换两个数字的位置,称为对换。
例如:排列12345(奇排列)和13245(偶排列)就是数字2和数字3的位置进行了对换。
注:①一个排列做偶数次对换,奇偶性不变;一个排列做奇数次对换,奇偶性会发生改变。特别地:一个排列经过1次对换,奇偶性会发生改变。
② 在 n \ n n级排列中,奇排列、偶排列的个数各有n ! 2 \frac{n!}{2}2n!个。
引言
学习 n \ n n阶行列式之前,我们可以先回顾一下二元一次方程组的求解过程。假设有二元一次方程组如下所示:
{ 5 x + 6 y = 7 9 x + 4 y = 3 \begin{cases} 5x+6y = 7 \\ 9x+4y = 3 \end{cases}{5x+6y=79x+4y=3
通常的思想是:用消元法求解 x \ x x和 y \ y y。
也就是分别将方程组变形为{ 5 × 9 x + 6 × 9 y = 7 × 9 ① 9 × 5 x + 4 × 5 y = 3 × 5 ② \begin{cases}5×9x+6×9y = 7×9\ ① \\9×5x+4×5y = 3×5\ ②\end{cases}{5×9x+6×9y=7×9 ①9×5x+4×5y=3×5 ②和{ 5 × 4 x + 6 × 4 y = 7 × 4 ① 9 × 6 x + 4 × 6 y = 3 × 6 ② \begin{cases}5×4x+6×4y = 7×4\ ① \\9×6x+4×6y = 3×6\ ②\end{cases}{5×4x+6×4y=7×4 ①9×6x+4×6y=3×6 ②,再分别用 ① − ② \ ①-② ①−②求得 x \ x x和 y \ y y的值,即: x = 3 × 6 − 7 × 4 9 × 6 − 5 × 4 , y = 7 × 9 − 3 × 5 9 × 6 − 5 × 4 \ x=\frac{3×6-7×4}{9×6-5×4} ,\ \ y=\frac{7×9-3×5}{9×6-5×4} x=9×6−5×43×6−7×4, y=9×6−5×47×9−3×5
假设我们定义一种新的运算:
∣ a b c d ∣ = a d − b c ( 1 ) \begin{vmatrix}a & b \\c & d\end{vmatrix}=ad-bc\ \ \ \ (1)∣∣∣∣acbd∣∣∣∣=ad−bc (1)
则上述 x \ x x和 y \ y y的值可以用新运算表示为:
x = ∣ 3 7 4 6 ∣ ∣ 9 5 4 6 ∣ , y = ∣ 7 3 5 9 ∣ ∣ 9 5 4 6 ∣ \ x=\frac{\begin{vmatrix}3 & 7 \\4 & 6\end{vmatrix}}{\begin{vmatrix}9 & 5 \\4 & 6\end{vmatrix}} ,\ \ y=\frac{\begin{vmatrix}7 & 3 \\5 & 9\end{vmatrix}}{\begin{vmatrix}9 & 5 \\4 & 6\end{vmatrix}} x=∣∣∣∣9456∣∣∣∣∣∣∣∣3476∣∣∣∣, y=∣∣∣∣9456∣∣∣∣∣∣∣∣7539∣∣∣∣
这里提到的新运算∣ a b c d ∣ = a d − b c \begin{vmatrix}a & b \\c & d\end{vmatrix}=ad-bc∣∣∣∣acbd∣∣∣∣=ad−bc,就是我们所要学习的二阶行列式的运算。
二阶行列式
二阶行列式通常写作:∣ a 11 a 12 a 21 a 22 ∣ \begin{vmatrix}a_{11} & a_{12} \\a_{21} & a_{22}\end{vmatrix}∣∣∣∣a11a21a12a22∣∣∣∣
① 对任一元素a i j a_{ij}aij,i ii是元素a i j a_{ij}aij的行标,j jj是元素a i j a_{ij}aij的列标。例如:a 11 a_{11}a11代表该行列式第1行第1列的元素。
② 主对角线(左)和次对角线(右)示例:
③ 二阶行列式运算可以简单记忆为:主对角线元素的乘积减去次对角线元素的乘积,用式子表示为:
∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 \begin{vmatrix}a_{11} & a_{12} \\a_{21} & a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}∣∣∣∣a11a21a12a22∣∣∣∣=a11a22−a12a21
小练习
(1) 计算∣ 1 3 7 9 ∣ \begin{vmatrix}1 & 3 \\7 & 9\end{vmatrix}∣∣∣∣1739∣∣∣∣的值
解:∣ 1 3 7 9 ∣ = 1 × 9 − 3 × 7 = − 12 \begin{vmatrix}1 & 3 \\7 & 9\end{vmatrix}=1×9-3×7=-12∣∣∣∣1739∣∣∣∣=1×9−3×7=−12
(2) 计算∣ 吱 美 女 雨 ∣ \begin{vmatrix}吱 & 美 \\女 & 雨\end{vmatrix}∣∣∣∣吱女美雨∣∣∣∣的值
解:∣ 吱 美 女 雨 ∣ = 吱 雨 一 美 女 \begin{vmatrix}吱 & 美 \\女 & 雨\end{vmatrix}=吱雨一美女∣∣∣∣吱女美雨∣∣∣∣=吱雨一美女
三阶行列式
与二阶行列式类似的,通常将三阶行列式写作:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ \begin{vmatrix}a_{11} & a_{12}& a_{13}\\a_{21} & a_{22}& a_{23}\\a_{31} & a_{32}& a_{33}\end{vmatrix}∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣
用画线法可以得到三阶行列式的求解结果:
我们可以发现上述结果具有:“三正、三负、共六项”的特点。
小练习
计算∣ 1 2 0 0 2 1 1 0 1 ∣ \begin{vmatrix}1 & 2 & 0\\0 & 2 & 1 \\ 1& 0 & 1\end{vmatrix}∣∣∣∣∣∣101220011∣∣∣∣∣∣的值
解:∣ 1 2 0 0 2 1 1 0 1 ∣ = 1 × 2 × 1 + 2 × 1 × 1 + 0 × 0 × 0 − 0 × 2 × 1 − 2 × 0 × 1 − 1 × 1 × 0 = 4 \begin{aligned}\begin{vmatrix}1 & 2 & 0\\0 & 2 & 1 \\ 1& 0 & 1\end{vmatrix}&=1×2×1+2×1×1+0×0×0-0×2×1-2×0×1-1×1×0\\&=4\end{aligned}∣∣∣∣∣∣101220011∣∣∣∣∣∣=1×2×1+2×1×1+0×0×0−0×2×1−2×0×1−1×1×0=4
由画线法,我们可以将三阶行列式展开为如下形式:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 13 a 21 a 32 + a 12 a 23 a 31 − a 13 a 22 a 31 − a 12 a 21 a 33 − a 11 a 23 a 32 = ① + ② + ③ − ④ − ⑤ − ⑥ \begin{aligned}\begin{vmatrix}a_{11} & a_{12}& a_{13}\\a_{21} & a_{22}& a_{23}\\a_{31} & a_{32}& a_{33}\end{vmatrix}&=a_{11}a_{22}a_{33}+a_{13}a_{21}a_{32}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}\\&= \ \ \ \ \ \ \ ①\ \ \ \ \ \ +\ \ \ \ \ \ ②\ \ \ \ \ \ +\ \ \ \ \ \ ③\ \ \ \ \ \ -\ \ \ \ \ \ ④\ \ \ \ \ \ -\ \ \ \ \ \ ⑤\ \ \ \ \ \ -\ \ \ \ \ \ ⑥\end{aligned}∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣=a11a22a33+a13a21a32+a12a23a31−a13a22a31−a12a21a33−a11a23a32= ① + ② + ③ − ④ − ⑤ − ⑥
观察展开式中的每一项,我们可以得到如下结果:
| 第 i 项 | 符号 | 行 标 | 列 标 | 列标的逆序数 |
|---|---|---|---|---|
| ① | + | 123 | 123 | 0(偶排列) |
| ② | + | 123 | 312 | 2(偶排列) |
| ③ | + | 123 | 231 | 2(偶排列) |
| ④ | - | 123 | 321 | 3(奇排列) |
| ⑤ | - | 123 | 213 | 1(奇排列) |
| ⑥ | - | 123 | 132 | 1(奇排列) |
由上述对比,我们可以发现,对于三阶行列式的展开式:
- 行标始终取为标准排列
- 列标取遍排列的所有可能
- 从不同行不同列取出三个元素相乘,其符号由列标排列的奇偶性决定
像这样的展开方式,我们称之为按行展开。
n \ n n阶行列式
由上述规律,我们可以很快的写出n阶行列式按行展开的式子:
∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ = ∑ j 1 , j 2 , ⋯ , j n ( − 1 ) N ( j 1 j 2 ⋯ j n ) a 1 j 1 a 2 j 2 ⋯ a n j n \begin{vmatrix}a_{11} & a_{12}& \cdots&a_{1n}\\a_{21} & a_{22}&\cdots& a_{2n}\\\vdots &\vdots& \ddots&\vdots\\ a_{n1} & a_{n2}& \cdots&a_{nn}\end{vmatrix}=\sum_{j_1,j_2,\cdots,j_n}(-1)^{N(j_1j_2 \cdots j_n)} a_{1j_1}a_{2j_2} \cdots a_{nj_n}∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann∣∣∣∣∣∣∣∣∣=j1,j2,⋯,jn∑(−1)N(j1j2⋯jn)a1j1a2j2⋯anjn
行列式通常用字母 D \ D D表示,上述 n \ n n阶行列式也可以直接写作: D = ∣ a i j ∣ \ D=|a_{ij} | D=∣aij∣
注:只有一个数的行列数,就代表这个数。例如:∣ a 11 ∣ = a 11 |a_{11}|=a_{11}∣a11∣=a11、∣ − 1 ∣ = − 1 |-1|=-1∣−1∣=−1(与绝对值符号相区别)
常见的几种三角行列式(除阴影部分有数值,其余部分都为0)
| 名称 | 形状 | 特点 |
|---|---|---|
| 上三角 |  | 以主对角线为分割,展开式为a 11 a 12 ⋯ a 1 n a_{11}a_{12}\cdots a_{1n}a11a12⋯a1n |
| 下三角 | 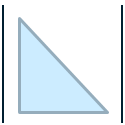 | 以主对角线为分割,展开式为a 11 a 12 ⋯ a 1 n a_{11}a_{12}\cdots a_{1n}a11a12⋯a1n |
| 对角形 |  | 以主对角线为分割,展开式为a 11 a 12 ⋯ a 1 n a_{11}a_{12}\cdots a_{1n}a11a12⋯a1n |
| 山寨上三角 |  | 以次对角线为分割,展开式为( − 1 ) n ( n − 1 ) 2 a 11 a 12 ⋯ a 1 n (-1)^{\frac{n(n-1)}{2}}a_{11}a_{12}\cdots a_{1n}(−1)2n(n−1)a11a12⋯a1n |
| 山寨下三角 | 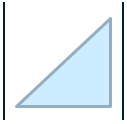 | 以次对角线为分割,展开式为( − 1 ) n ( n − 1 ) 2 a 11 a 12 ⋯ a 1 n (-1)^{\frac{n(n-1)}{2}}a_{11}a_{12}\cdots a_{1n}(−1)2n(n−1)a11a12⋯a1n |
| 山寨对角形 |  | 以次对角线为分割,展开式为( − 1 ) n ( n − 1 ) 2 a 11 a 12 ⋯ a 1 n (-1)^{\frac{n(n-1)}{2}}a_{11}a_{12}\cdots a_{1n}(−1)2n(n−1)a11a12⋯a1n |
小练习
将行列式 D 1 = ∣ 1 2 3 8 1 1 0 4 2 2 0 5 1 0 0 9 ∣ \ D_1=\begin{vmatrix}1 & 2& 3&8\\1 & 1&0& 4\\2 &2& 0&5\\ 1 & 0& 0&9\end{vmatrix} D1=∣∣∣∣∣∣∣∣1121212030008459∣∣∣∣∣∣∣∣按行展开。
参考文献
[1] 宋浩.《线性代数》全程高清教学视频 “惊叹号”系列[EB/OL].https://www.bilibili.com/video/av29971113?from=search&seid=4757026773102990321,2019-6-12.
下篇笔记地址→ 行列式性质