高斯消元法 求解线性方程组

小辣鸡第一次发文，欢迎大家指正！?

搬来题干： 线性方程组求解输入是 N（N<256）元线性方程组 Ax=B，输出是方程组的解，也可能无解或有多组解。可以用高斯消去法求解，也可以采用其它方法。

高斯消元法的主要思路：

• 1.将含有系数的行列式（m*(m+1))（多了后面的常数）转换成上三角

• 转换过程中又分成几步：

• a. 针对每列，找到绝对值最大的一行与本行互换*(目的后面会讲到)

• b.互换后，将该列下面的元素变为0

• 变为0的方法是：找到两个之间的倍数关系，做差（具体见下实例）

• c.沿m*m的对角线依次进行a,b操作

• 2.将各参数带入，回代求未知数的值

其中对解的处理：a*x=b

若a=0,b=0,无穷解；
若a=0，b!=0,无解；
若a!=0,b=0,则该x=0;

• 举个例子吧！

• 用到的关于行列式的性质：

• 把行列式某一行的元素乘以同一个数后加到另一行的对应元素上，行列式不变。

1.将含有系数的行列式（m*(m+1))（多了后面的常数）转换成上三角

a步骤代码：

绝对值最大：第j行第i个数若为零或接近于零，计算机将“溢出”而停止计算，或产生较大误差。

for (int j = 0; j < n; j++)   //注意是N
        {
            int Un = 0;
            int l = 0;//记录行
            //找绝对值最大的一行
            for (int i = j; i < n; i++)
            {
                if (Un <= abs(un[i][j]))
                {
                    Un = abs(un[i][j]);
                    l = i;
                }
            }
            //把l行和第j行对调
            for (int i = j; i < n + 1; i++)
            {
                swap(un[j][i], un[l][i]);
                /*int t = un[j][i];
                un[j][i] = un[l][i];
                un[l][i] = t;*/
​
            }

b步骤代码：

//变0  
            for (int i = j + 1; i < n&&un[j][j]!=0&&un[i][j]!=0; i++)
            {
                double temp = un[i][j] / un[j][j];
                for (int k = j; k< n + 1; k++)
                {
                    un[i][k] -= temp * un[j][k];
                    if (abs(un[i][k]) <= 1e-15)//精度问题 0
                        un[i][k] = 0;
                }
            }

c步骤是包括a b的循环；

2.将各参数带入，回代求未知数的值

for (int i = n - 1; i >= 0; i--)
        {
            double sum = 0;
            for (int j = i + 1; j < n; j++)
            {
                sum += un[i][j] * x[j];
            }
            un[i][n] -= sum;
            if (un[i][i])
            {
                x[i] = un[i][n] / un[i][i];
                if (abs(x[i]) <= 1e-15)//精度问题 0
                    x[i] = 0;
            }
            else {
                if (un[i][n])
                {
                    cout << "无解！" << endl;
                    t = 0;
                    break;
​
                }
                    
                else
                {
                    cout << "有无穷解" << endl << "其中一组解为：》》"<<endl;
                    x[i] = 1;
                }
​
            }

全部代码奉上：

//线性方程组求解
#include<iostream>
#include<vector>
#include<algorithm>
​
using namespace std;
​
double un[256][257];
double x[256];
​
int main()
{
    //输入方程组
    int n;
    bool t = 1;
    while (cin >> n)
    {
        //n行 N+1列
        //vector<vector<int>>un(n, vector<int>(n + 1));
        double un[256][257];
        double x[256];//答案
​
        //输入系数
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n + 1; j++)
            {
                cin >> un[i][j];
            }
        }
    //化为上三角矩阵
        for (int j = 0; j < n; j++)   //注意是N
        {
            int Un = 0;
            int l = 0;//记录行
            //找绝对值最大的一行
            for (int i = j; i < n; i++)
            {
                if (Un <= abs(un[i][j]))
                {
                    Un = abs(un[i][j]);
                    l = i;
                }
            }
            //把l行和第j行对调
            for (int i = j; i < n + 1; i++)
            {
                swap(un[j][i], un[l][i]);
                /*int t = un[j][i];
                un[j][i] = un[l][i];
                un[l][i] = t;*/
​
            }
            //变0  
            for (int i = j + 1; i < n&&un[j][j]!=0&&un[i][j]!=0; i++)
            {
                double temp = un[i][j] / un[j][j];
                for (int k = j; k< n + 1; k++)
                {
                    un[i][k] -= temp * un[j][k];
                    if (abs(un[i][k]) <= 1e-15)//精度问题 0
                        un[i][k] = 0;
                }
            }
            
        }
        cout << endl;
        /*cout << "_____________________________" << endl;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n + 1; j++)
            {
                cout << un[i][j] << " ";
            }cout << endl;
        }*/
​
​
        //回代求值
        
        for (int i = n - 1; i >= 0; i--)
        {
            double sum = 0;
            for (int j = i + 1; j < n; j++)
            {
                sum += un[i][j] * x[j];
            }
            un[i][n] -= sum;
            if (un[i][i])
            {
                x[i] = un[i][n] / un[i][i];
                if (abs(x[i]) <= 1e-15)//精度问题 0
                    x[i] = 0;
            }
            else {
                if (un[i][n])
                {
                    cout << "无解！" << endl;
                    t = 0;
                    break;
​
                }
                    
                else
                {
                    cout << "有无穷解" << endl << "其中一组解为：》》"<<endl;
                    x[i] = 1;
                }
​
            }
        }
        
        cout << "_____________________________" << endl;
        
            for (int i = 0; i < n&&t; i++)
            {
                cout << "X" << i + 1 <<" = " << x[i] << " ";
            }
        }
        return 0;
    }

测试结果如下：

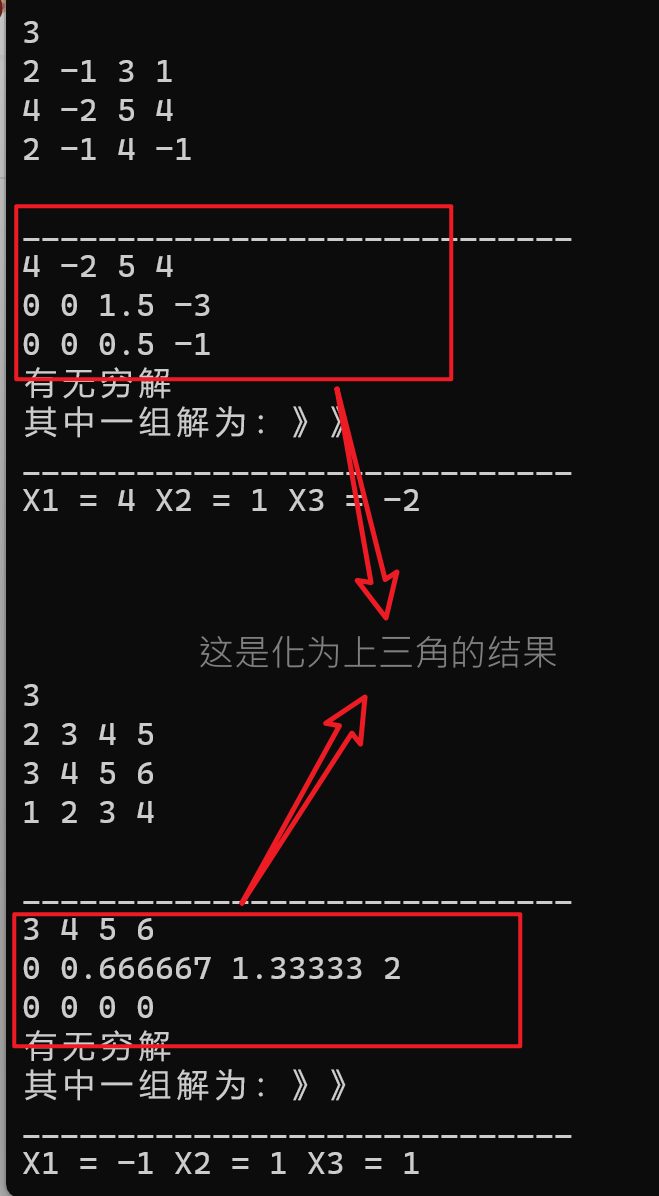
欢迎评论区留言?