稳定性:如果a原本在b前面,而a=b,排序之后a仍然在b的前面则为稳定,排序之后 a 可能会出现在 b 的后面即为不稳定。
不稳定的排序算法:快速排序,希尔排序,选择排序和堆排序。
时间复杂度如下:图来源于https://zhuanlan.zhihu.com/p/73714165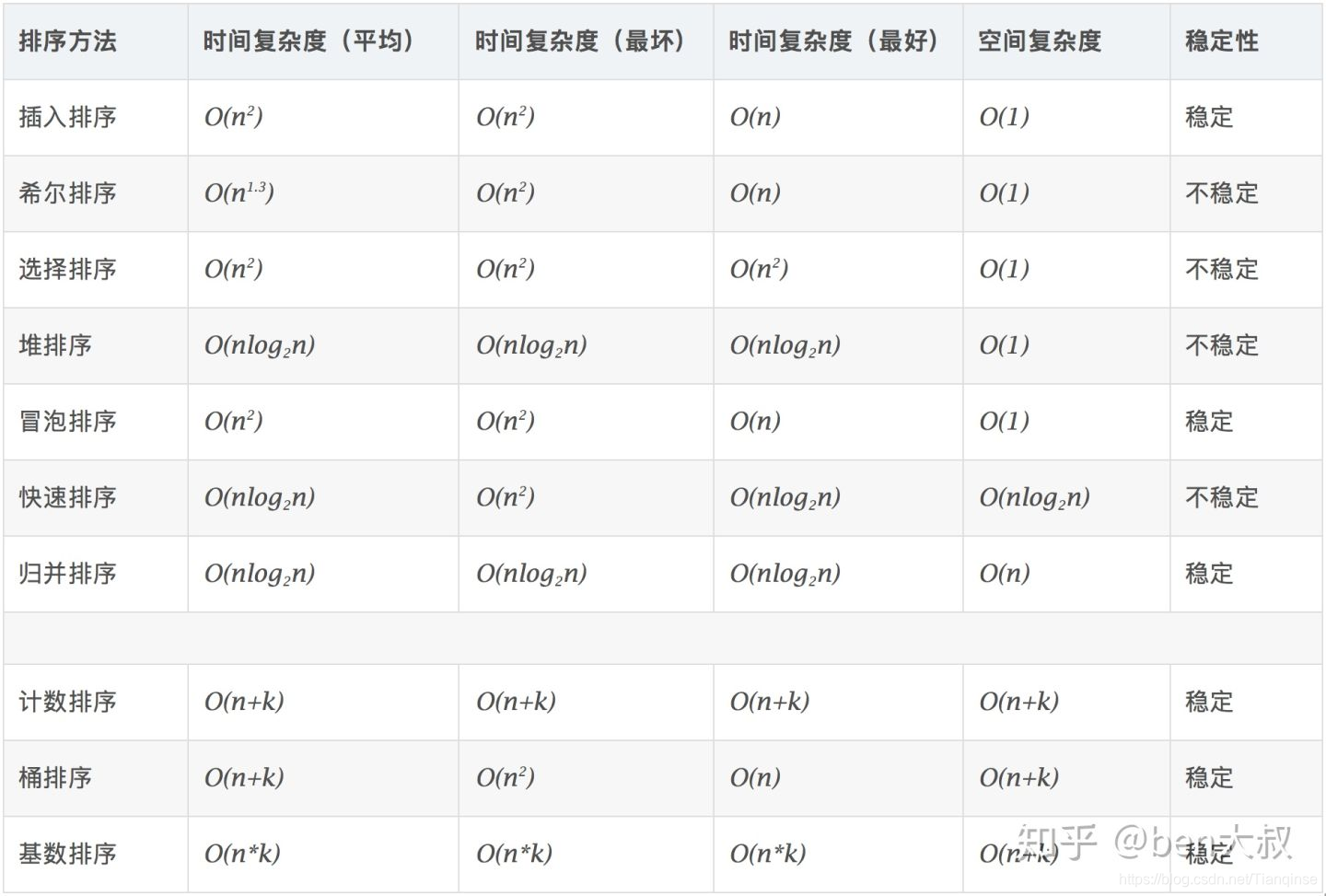
1.插入排序
插入排序是将每一个元素都与前面的元素比较,小的放在前面。
代码如下:
void insert_sort(vector<int> &num)
{
int len=num.size();
for(int i=0;i<len;++i)
for(int j=i;j>0&&num[j]<num[j-1];--j)
{
swap(num[j],num[j-1]);
}
}
最好情况:原数组是一个有序数组,时间复杂度O(N);
最好情况:原数组是一个逆序数组,时间复杂度O(NN);
平均时间复杂度:O(NN);
2.冒泡排序
从数组中第一个数开始,依次遍历数组中的每一个数,通过相邻比较交换,每一轮循环下来找出剩余未排序数的中的最大数并“冒泡”至数列的顶端。
void bubble_sort(vector<int> &num)
{
int len=num.size();
for(int i=len;i>0;--i)
{
for(int j=1;j<i;++j)
{
if(num[j]<num[j-1])
swap(num[j],num[j-1]);
}
}
}
最好情况:原数组是一个有序数组,时间复杂度O(N);
最好情况:原数组是一个逆序数组,时间复杂度O(NN);
平均时间复杂度:O(NN);
3.选择排序
从所有记录中选出最小的一个数据元素与第一个位置的记录交换;然后在剩下的记录当中再找最小的与第二个位置的记录交换,循环到只剩下最后一个数据元素为止。
void select_sort(vector<int> &num)
{
int len=num.size();
for(int i=0;i<len;++i)
{
int pos=i;
for(int j=i;j<len;++j)
{
if(num[j]<num[pos])
swap(num[j],num[pos]);
}
}
}
最好情况:原数组是一个有序数组,时间复杂度O(NN);
最好情况:原数组是一个逆序数组,时间复杂度O(NN);
平均时间复杂度:O(N*N);
4.希尔排序
希尔排序法是对相邻指定距离(称为增量)的元素进行比较,并不断把增量缩小至1,完成排序。
希尔排序开始时增量较大,分组较多,每组的记录数目较少,故在各组内采用直接插入排序较快,后来增量di逐渐缩小,分组数减少,各组的记录数增多,但由于已经按di−1分组排序,文件叫接近于有序状态,所以新的一趟排序过程较快。因此希尔 排序在效率上比直接插入排序有较大的改进。
在直接插入排序的基础上,将直接插入排序中的1全部改变成增量d即可,因为希尔排序最后一轮的增量d就为1。
平均时间复杂度:希尔排序算法的时间复杂度分析比较复杂,实际所需的时间取决于各次排序时增量的个数和增量的取值。时间复杂度在O(n ^ 1.3)到O(n ^ 2)之间。
5.堆排序
堆:
1、完全二叉树或者是近似完全二叉树。
2、大顶堆:父节点不小于子节点键值,小顶堆:父节点不大于子节点键值。左右孩子没有大小的顺序。
堆排序在选择排序的基础上提出的,步骤:
1、建立堆
2、删除堆顶元素,同时交换堆顶元素和最后一个元素,再重新调整堆结构,直至全部删除堆中元素。
6.快速排序
快速排序是采用分治的思想,设置一个键值,大于它的放在右边,小于它的放在左边,然后对左右两个数组进行递归,重复同样的操作。
代码如下:
void quick_sort(vector<int> &num,int l,int r)
{
int first=l,last=r-1,key=num[first];
if(l+1>=r)
return ;
while(first<last)
{
while(first<last&&num[last]>=key)
last--;
num[first]=num[last];
while(first<last&&num[first]<=key)
first++;
num[last]=num[first];
}
num[first]=key;
quick_sort(num,l,first);
quick_sort(num,first+1,r);
}
快速排序的时间性能取决于快速排序递归的深度,可以用递归树来描述递归算法的执行情况。
最坏情况:递归树是一颗斜树,最大深度为n,交换次数n-i,时间复杂度O(NN);
比如排序好的从大到小数组,现在要从小到大排序。
最好情况:递归树分布很均匀,深度为nlongn,交换次数n-i,
时间复杂度O(NlongN);
平均时间复杂度:O(N*longN);
就空间复杂度来说,主要是递归造成的栈空间的使用,最好情况,递归树的深度为log2n,其空间复杂度也就为O(logn),最坏情况,需要进行n‐1递归调用,其空间复杂度为O(n),平均情况,空间复杂度也为O(logn)。