引言

本文主要针对作者本人复习使用，相关基础知识点不会讲述。

二叉堆

二叉堆是最普通的堆，能够实现$push,pop$等基本操作，下面以小根堆为例给出一种常见的实现。

首先设置一个足够大的数组，我们将树的节点按照层次遍历的顺序从小到大依次放置在数组中，数组中的位置也对应是该节点的编号，如下图所示：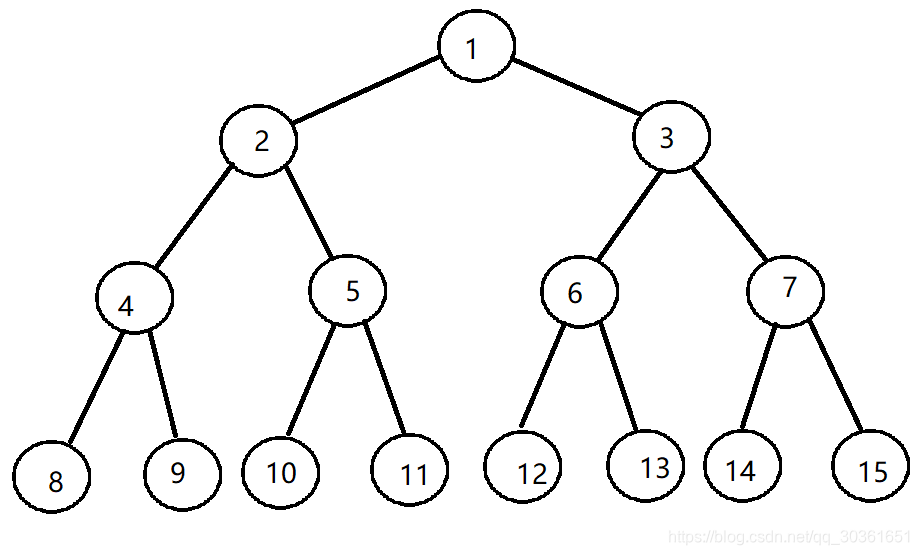

上图是一个典型的二叉树，每个节点上标注的数字即是该节点的编号，容易发现对于一个节点$u$而言，它的儿子分别是$2u,2u+1$，它的父亲是$\lfloor \frac{u}{2}\rfloor$。
下面是一些必要的数组和变量声明，其中$t[maxn]$数组用于储存堆，$tot$表示节点的最大编号。

int t[maxn],tot;

由于小根堆必须满足父亲节点的权值不小于子节点的权值，因此再$push$和$pop$的过程中要对这一性质进行有效地维护。

$push$操作： 考虑插入一个权值为$x$的点，首先直接将$x$插入到数组的末尾即可，以上图为例，插入一个新点后如下图所示，新点用红色表示：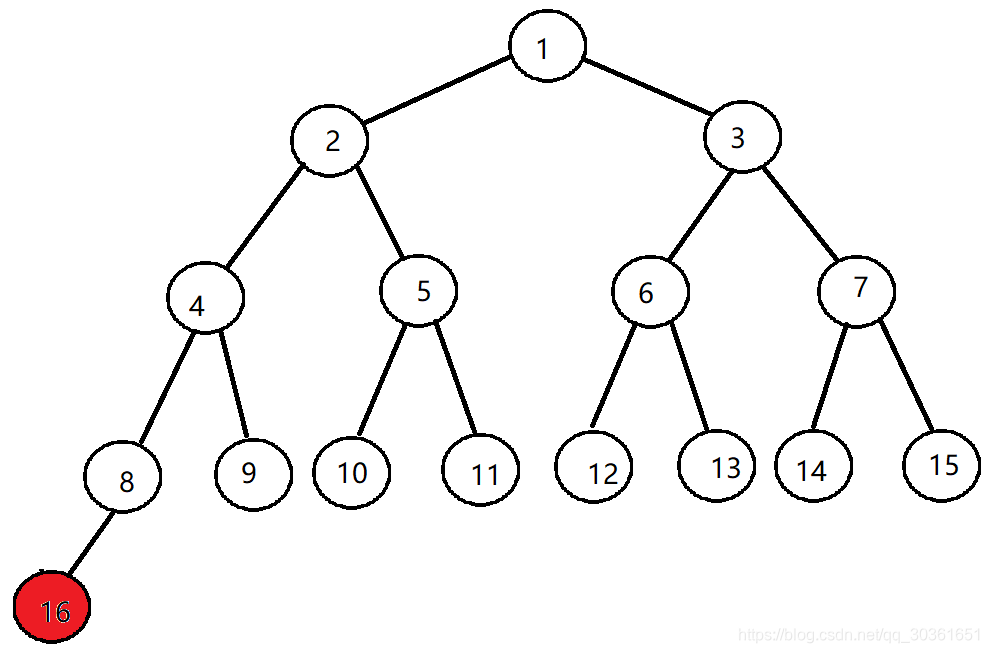

由于插入一个新点后的新堆可能不满足堆的性质，因此考虑交换一些节点的权值来达到平衡，考虑上图中的$16、8$两个节点，如果$8$节点权值大于$16$节点，那么我们交换它们两个的权值即可，然后再考虑$8$与$4$权值的关系…一直比较到满足父亲权值不大于儿子权值的时候为止。

具体实现代码如下：

void push(int x){
	t[++tot]=x;//新建节点并赋予权值
	int u=tot;//从该新节点开始考虑其与父亲的关系
	while(u>1){
		int v=u>>1;
		if(t[u]<t[v])swap(t[u],t[v]);else return;
		u=v;
	}
}

$pop$操作： 先将树根节点与编号最大的节点的权值进行交换，然后将这个编号最大的节点删除即可。
当然这样做并不能保证新的堆仍然具有良好的性质，因此考虑根节点是否符合性质，即根节点权值必须不大于它的两个儿子节点，如果不满足，那么考虑将它的两个儿子中较小的一个与它交换一下权值，然后类似于$push$操作一样继续向下考虑直到考虑到满足条件位置。不过需要注意一下没有儿子以及只有一个儿子的情况，需要特殊判断，代码实现如下：

void pop(){
	swap(t[1],t[tot]);--tot;//先将根节点与尾节点交换权值并删除尾节点
	int u=1;
	while((u<<1)<=tot){//如果存在儿子
		int a=u<<1,b=a+1;//两个儿子分别是a,b
		if(t[a]>t[u] && (b>tot || b<=tot && t[b]>t[u]))return;//如果符合堆的性质那么就不用继续判断了
		if(b>tot || t[a]<=t[b]){//如果只有一个儿子或左儿子不大于右儿子，就跟左儿子交换即可
			swap(t[a],t[u]);
			u=a;
		}else swap(t[b],t[u]),u=b;//否则跟右儿子交换
	}
}

下面以LuoGu P3378 【模板】堆为例给出一份参考代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
int t[maxn],n,tot;
void push(int x){
	t[++tot]=x;
	int u=tot;
	while(u>1){
		int v=u>>1;
		if(t[u]<t[v])swap(t[u],t[v]);else return;
		u=v;
	}
}
void pop(){
	swap(t[1],t[tot]);--tot;
	int u=1;
	while((u<<1)<=tot){
		int a=u<<1,b=a+1;
		if(t[a]>t[u] && (b>tot || b<=tot && t[b]>t[u]))return;
		if(b>tot || t[a]<=t[b]){
			swap(t[a],t[u]);
			u=a;
		}else swap(t[b],t[u]),u=b;
	}
}
int top(){
	return t[1];
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		int op,x;
		scanf("%d",&op);
		if(op==1){
			scanf("%d",&x);
			push(x);
		}else if(op==2)printf("%d\n",top());
		else pop();
	}
} 

左偏树

左偏树是一种可并堆，能够将两个堆进行合并，形成的一个新的堆仍然具有良好的性质。

首先给出几个定义：
外节点： 没有儿子或者只有一个儿子的节点
$d[u]$： 从$u$节点出发到达最近的外节点的距离

规定外节点的$d$值为$0$，空节点的$d$值也就是-1，相应地一开始要设置$d[0]=-1$。

那么左偏树除了满足堆的性质以外，还满足它的左儿子的$d$值不小于右儿子的$d$值，我们在建树的时候就需要额外维护这种性质。

然后注意到一颗大小为$n$的树它的根节点的$d$值的级别是$O(log(n+1))$的，因为假设它的$d$值是$x$，那么这颗树至少在前$x+1$层都是满的，也就是说至少有$2^{x+1}-1$个节点。

关于左偏树最核心的操作是$merge$操作，它能够将两个左偏树合并为一个左偏树，每次都拿右儿子去合并即可，这样能够保证$d$值递减，而$d$值最大是$O(logn)$级别的，这样就能保证$merge$是对数级别的复杂度，有时候为了方便需要记录每个节点的父节点，这个用于并查集的更新，就能够很快地找到每个节点所在左偏树的根节点。下面给出一份实现代码：

int merge(int u,int v){
	if(!u || !v)return u+v;
	if(val[u]>val[v])swap(u,v);
	rs[u]=merge(rs[u],v);
	fa[rs[u]]=u;//更新fa数组，当需要用到并查集的时候才写这一句
	if(d[rs[u]]>d[ls[u]])swap(rs[u],ls[u]);//保证右子树的d值更小
	d[u]=d[rs[u]]+1;
	return u;
}

$push$节点和$pop$节点的操作均可以用$merge$操作实现。如果要$push$节点那么可以$merge(root,newnode)$即可，如果要$pop$节点那就将$root$的两个儿子节点$merge$一下即可。具体代码如下所示：

int newnode(int x){
	val[++tot]=x;
	return tot;
}
void push(int x){
	root=merge(root,newnode(x));
}
void pop(){
	root=merge(ls[root],rs[root]);
}

当然，有了并查集我们还可以维护多个左偏树，如果想要$pop$某个节点所在的左偏树，可以利用并查集锁定该节点所在的左偏树的根节点即可，不过断开根节点和它儿子节点的边会导致并查集出现问题，需要更改一些$fa$值，考虑设置根节点的两个儿子节点的$fa$为它们自己，而根节点的$fa$需要设置为新树的根节点，最后还需要给原树的根节点打上一个被删除标记，代码如下所示：

void pop(int u){//pop u所在的左偏树
	if(vis[u])return;//如果已经被删除就不需要进一步操作了
	u=fd(u);//找到u所在左偏树根节点
	fa[rs[u]]=rs[u];//儿子的fa设置为自己
	fa[ls[u]]=ls[u];
	fa[u]=merge(ls[u],rs[u]);//根节点的fa设置成新树的根节点
	vis[u]=1;//给根节点打上被删除标记
}

左偏树还可以实现删除任意一个节点的操作，我们考虑增加一个$f$数组，用于储存左偏树中的每个节点的直接父亲(注意与并查集中的父亲节点区分开)，假设我们要删除$u$节点，那么需要设置$f[merge(ls[u],rs[u])]=f[u]$，此外还要更改一下$f[u]$的儿子节点，并且注意当$u$是根节点的时候要特判一下，设置一下$root$值为新树根节点。不过注意到在$f[u]$之上的节点的$d$值没有得到维护，因此需要暴力跳父亲节点去$check$是否满足左偏树的性质，并进行相应地更新即可，注意到之后$d$值不符合的时候才会继续暴跳父亲节点，一旦有一个父亲节点满足$d$值关系，那么就没有必要继续跳了，这样的话$d$值最多被更新$O(logn)$次，复杂度得到了保证，如果需要维护并查集的话注意特判一下$u$是根节点的情况，代码实现如下所示：

void del(int u){
	if(vis[u])return;int v;
	f[v=merge(ls[u],rs[u])]=f[u];
	if(u==root){
		root=v;
		fa[u]=fa[v]=v;
	}
	if(ls[f[u]]==u)ls[f[u]]=v;else rs[f[u]]=v;
	while(f[v]){
		v=f[v];
		if(d[ls[v]]<d[rs[v]])swap(ls[v],rs[v]);
		if(d[v]==d[rs[v]]+1)return;
		d[v]=d[rs[v]]+1;
	}
}

左偏树还有一种随机化的写法，也就是在$merge$操作中随机交换左右儿子，而不是根据$d$值来决定是否交换，可以证明这样写的话复杂度仍然是$O(logn)$的。

最后注意左偏树的深度其实并不保证是$O(logn)$的，甚至能够到达$O(n)$，即一条向左倾斜的链。

下面以LuoGu P3377 【模板】左偏树（可并堆）为例给出一份参考代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e5+5;

int fa[maxn],ls[maxn],rs[maxn],val[maxn],d[maxn],n,m,vis[maxn];

int fd(int rt){
	return rt==fa[rt]?rt:(fa[rt]=fd(fa[rt]));
}
int merge(int u,int v){
	if(!u || !v)return u+v;
	if(val[u]>val[v] || val[u]==val[v]&&u>v)swap(u,v);
	fa[rs[u]=merge(rs[u],v)]=u;
	if(d[rs[u]]>d[ls[u]])swap(rs[u],ls[u]);
	d[u]=d[rs[u]]+1;
	return u;
}
int pop(int u){
	if(vis[u])return -1;
	u=fd(u);
	fa[rs[u]]=rs[u];
	fa[ls[u]]=ls[u];
	fa[u]=merge(ls[u],rs[u]);
	vis[u]=1;
	return val[u];
}
int main(){
	d[0]=-1;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i){
		scanf("%d",&val[i]);
		fa[i]=i;
	}
	for(int i=1;i<=m;++i){
		int op,x,y;
		scanf("%d%d",&op,&x);
		if(op==1){
			scanf("%d",&y);
			if(fd(x)==fd(y) || vis[x] || vis[y])continue;
			merge(fd(x),fd(y));
		}else{
			printf("%d\n",pop(x));
		}
	}
}

斜堆

斜堆是左偏堆的一个变种，唯一的差别就是$merge$函数。斜堆不储存$d$值，并且不依靠$d$值来判断是否需要交换左右儿子，而是每次递归回溯都直接交换左右儿子，代码如下所示：

int merge(int u,int v){
	if(!u || !v)return u+v;
	if(val[u]>val[v])swap(u,v);
	rs[u]=merge(rs[u],v);
	fa[rs[u]]=u;//更新fa数组，当需要用到并查集的时候才写这一句
	swap(rs[u],ls[u]);//直接交换左右儿子
	return u;
}

剩下的操作和左偏树相同，就不多说，需要注意的是斜堆的深度同样无法得到保证，但它的复杂度可以保证$O(logn)$。

配对堆

配对堆的均摊复杂度是$O(logn)$的，但实际上它的插入操作非常快，不过删除操作就较为逊色，它也是一种可并堆，能够将两个堆进行合并，除此之外它还能实现更键值(由大变小)的操作。

配对堆采用左儿子右兄弟的方式储存树结构，设置$son[u]$表示$u$的左儿子，$bro[u]$表示$u$的右兄弟，具体如下图所示：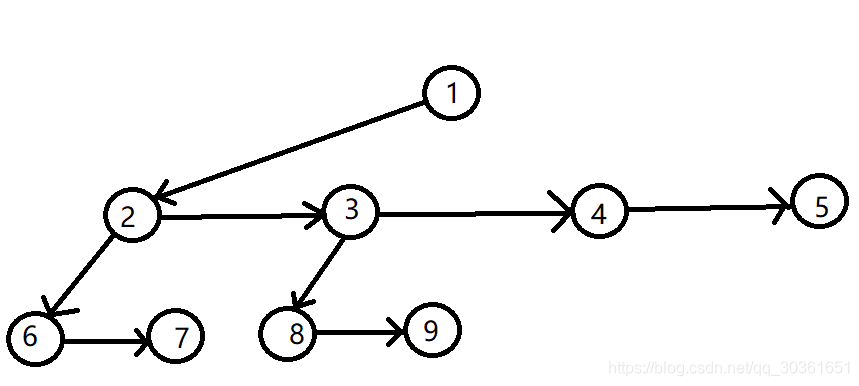

上图中以$2$节点为例，$bro[2]=3,son[2]=6$，如果一个节点没有兄弟节点，那么设置其兄弟节点值为0，儿子节点没有同理。此外再设置一个$fa$数组，注意到上图中每个节点最多只有一个节点指向它，考虑让这个指向它的节点是它的$fa$值，这只是为了方便起见这样做，事实上从一颗树的角度来说它的父亲不应该这样设置。

下面来实现$merge$操作，假设要将$u$和$v$合并，并且$val[u]\le val[v]$(如果不满足就交换一下)，那么设置$fa[v]=u,fa[son[u]]=v,bro[v]=son[u],son[u]=v$即可，如下图所示(加入以10节点为根新树，假设$val[1]\le val[10]$，将灰线断开，连上红线)：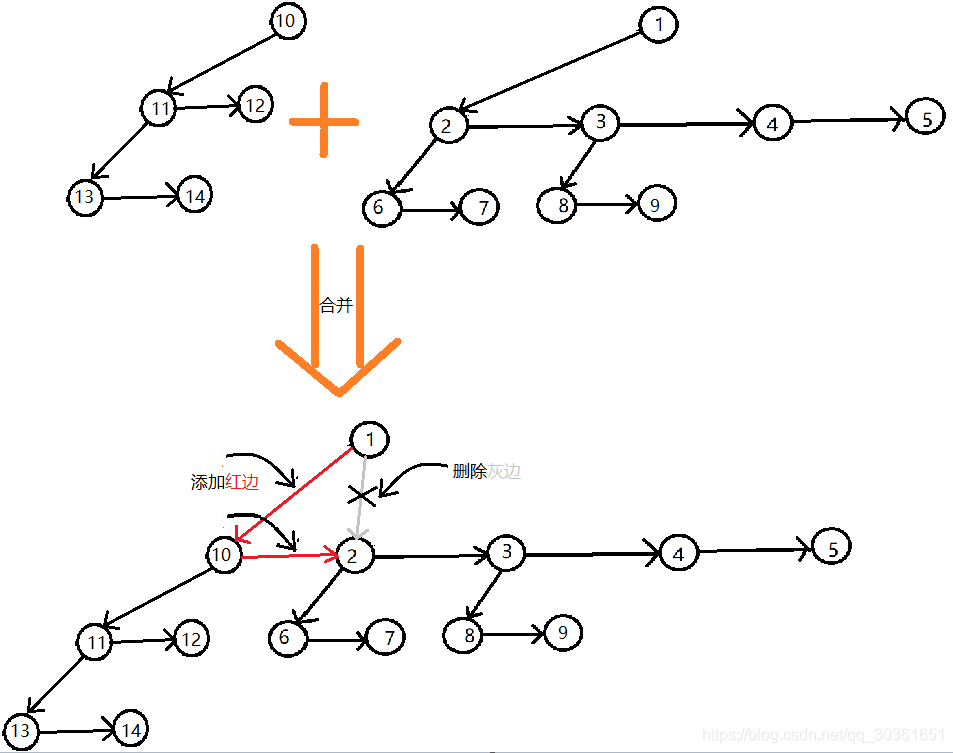

具体代码如下：

int merge(int u,int v){
	if(!u || !v)return u+v;
	if(val[u]>val[v])swap(u,v);
	fa[son[u]]=v;
	fa[v]=u;
	fa[u]=0;
	bro[v]=son[u];
	son[u]=v;
	return u;
}

有了$merge$操作，实现$push$操作就很简单了，类似左偏树，我们$merge(root,newnode)$即可。代码如下：

int newnode(int x){
	val[++tot]=x;
	return tot;
}
void push(int x){
	root=merge(root,newnode(x));
}

最麻烦的是$pop$操作，注意到$push$操作是$O(1)$的，那么复杂度全堆到了$pop$操作上。我们考虑$merge$根节点的所有儿子节点，注意到这里的儿子节点指的是树的关系中的儿子节点，还是以下面这张图为例，我们需要将$2、3、4、5$节点$merge$。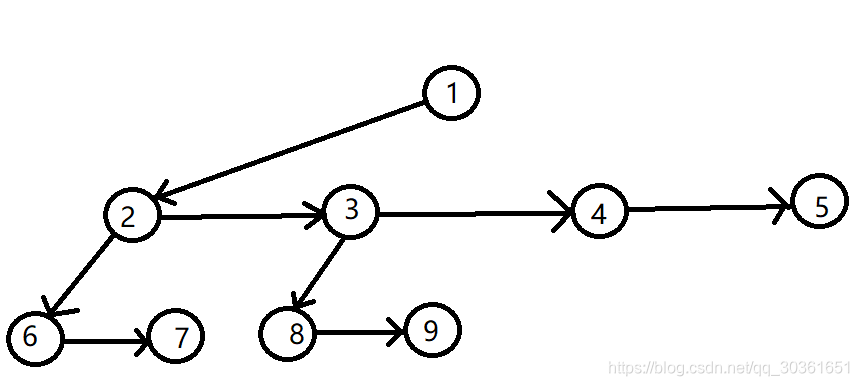

如果一个一个$merge$的话复杂度会太大，考虑从左到右两个两个$merge$，再从右到左依次merge，这里先实现一个辅助函数$merges(u)$用于合并它的所有兄弟节点，代码如下所示：

int merges(int u){//将u的兄弟全部合并,从左到右两两配对，再从右往左依次合并 
	fa[u]=0;
	if(!u || !bro[u])return u;
	int v=bro[u],w=bro[v];
	fa[v]=bro[u]=bro[v]=0;
	return merge(merge(u,v),merges(w));
}

那么$pop$操作其实就是$merges$它的左儿子即可。代码如下：

void pop(){
	root=merges(son[root]);
}

配对堆还可以减小某个节点的值，方法也很暴力，考虑减小某个节点的值后，直接将该节点连同其子树从原树中分离，然后再与原树进行$merge$操作即可，原理也比较简单，也不多解释， 具体看代码：

void assign(int u,int x){
	val[u]=x;
	if(!fa[u]){//如果是根节点就特判
		root=u;
		return;
	}
	if(son[fa[u]]==u){//判断一下与其父节点关系(兄弟or儿子)
		son[fa[u]]=bro[u];
	}else bro[fa[u]]=bro[u];
	fa[bro[u]]=fa[u];
	fa[u]=0;
	root=merge(root,u);//最后merge一下即可
}

这里以LuoGu P3378 【模板】堆为例给出一份参考代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e6+5;

int n,fa[maxn],tot,val[maxn],son[maxn],bro[maxn],root=0;

int merge(int u,int v){
	if(!u || !v)return u+v;
	if(val[u]>val[v])swap(u,v);
	fa[son[u]]=v;
	fa[v]=u;
	fa[u]=0;
	bro[v]=son[u];
	son[u]=v;
	return u;
}
int merges(int u){//将u的兄弟全部合并,从左到右两两配对，再从右往左依次合并 
	fa[u]=0;
	if(!u || !bro[u])return u;
	int v=bro[u],w=bro[v];
	fa[v]=bro[u]=bro[v]=0;
	return merge(merge(u,v),merges(w));
}

int newnode(int x){
	val[++tot]=x;
	return tot;
}
void push(int x){
	root=merge(root,newnode(x));
}
int top(){
	return val[root];
}
void pop(){
	root=merges(son[root]);
}
void assign(int u,int x){
	val[u]=x;
	if(!fa[u]){
		root=u;
		return;
	}
	if(son[fa[u]]==u){
		son[fa[u]]=bro[u];
	}else bro[fa[u]]=bro[u];
	fa[bro[u]]=fa[u];
	fa[u]=0;
	root=merge(root,u);
}

int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		int op,x;
		scanf("%d",&op);
		if(op==1){
			scanf("%d",&x);
			push(x);
		}else if(op==2)printf("%d\n",top());
		else pop();
	} 
} 

二项堆

二项堆是一种可并堆。
二项堆不是一棵树，而是一个森林，定义在这个森林中允许存在的最小的树是$B_0$，大小为$2^0$，即只有一个节点，$B_1$由两个$B_0$堆叠而来，$B_2$由两个$B_1$堆叠而来…以此类推类推，下面这张图可以很好地看出森林中树之间的关系。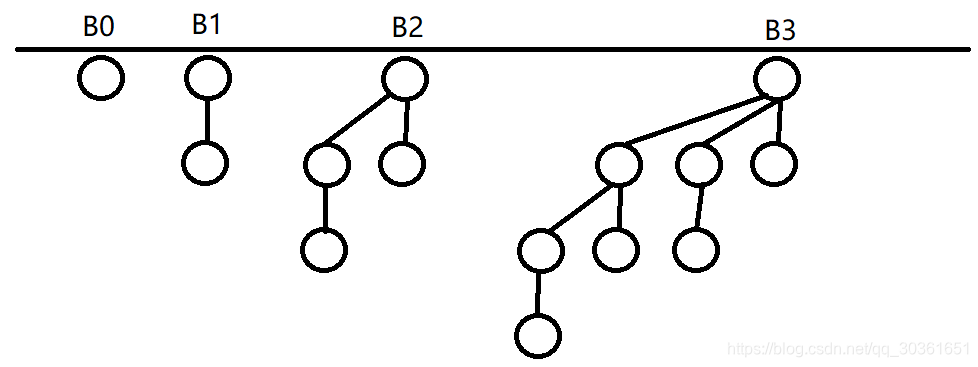

一个堆会被拆分成一个森林，并且该森林中的树只能是上图所示的树中的一些组成。比如一个大小为$7$的堆只能由$B_0,B_1,B_2$组成，一个大小为$9$的堆只能由$B_0,B_3$组成，其中每颗树都符合堆的性质。

具体实现的时候，为了方便我们用左儿子右兄弟的方法表示一颗树，即真实的树如下图所示：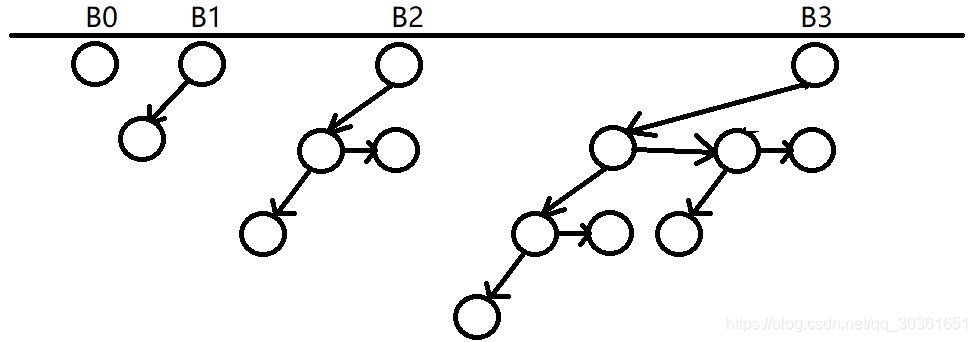

我们用一个结构体来记录二项堆，其本质是记录这个森林中所有树的根节点，并与此同时维护整个森林的最小值，即所有树根节点的$val$值种最小的一个，森林中最大的一棵树是$B_{sz-1}$。

struct Bheap{
	int t[maxlog]={},sz=0,top=0;
};

下面考虑实现$merge$操作，$merge$操作由两个引用参数$a,b$，代表将两个二项堆$a$与$b$合并，并将合并的结果放在$a$中。合并的原理也很简单，我们遍历两个森林的根节点列表按照尺寸从小到大的顺序，考虑$B_i$在$a,b$中是否存在，有四种情况，下面将分别讨论这四种情况，我们需要用到一个辅助函数$combin(u,v)$代表将两个相同大小的树合并，返回新树的根节点，此外需要一个变量$cur$代表在考虑$1\sim i-1$的尺寸的树的过程中产生的一个尺寸为$i$的树的根节点：

1. a存在，b存在：如果$cur$不为零，我们就将$cur$与$b$做一次$combin$操作，得到的新的$cur$显然尺寸为$i+1$，那么不能放在第$i$个位置，就到下一个位置继续考虑。如果$cur$为零，那么我们将$a$与$b$的$B_i$做一次$combin$操作，得到的根节点赋给$cur$，这时候$cur$的尺寸为$i+1$，也不能放在当前位置，考虑将$a$的$B_i$置空即可，然后考虑下一个位置能否放置$cur$。
2. a存在，b不存在：如果$cur$为零，我们什么都不要做；否则我们我们将$a$的$B_i$与$cur$做一次$combin$并更新$cur$，然后置空$a$的$B_i$。
3. a不存在，b存在：如果$cur$为零，我们把$b$的$B_i$赋给$a$的$B_i$即可；否则我们我们将$b$的$B_i$与$cur$做一次$combin$并更新$cur$。
4. a和b都不存在：如果$cur$为零，什么都不做。否则把$cur$直接赋给$a$的$B_i$即可。

那么$combin$操作如何实现呢？很简单，我们只需要比较$u,v$的$val$值大小，将$val$值小的作为新树根节点，然后另一个节点成为新树根节点的左儿子即可。
最后注意在$merge$的时候维护一下$top$即可。
代码如下所示：

int combin(int u,int v){//将相同大小的树合并
	if(!u || !v)return u+v;
	if(val[u]>val[v])swap(u,v);
	bro[v]=son[u];
	son[u]=v;
	return u;
}

void merge(Bheap &a,Bheap &b){
	if(!a.sz){//特判一下空堆的情况
		a=b;return;
	}else if(!b.sz)return;
	int i=0,cur=0;a.top=min(a.top,b.top);//维护一下top
	while(i<max(a.sz,b.sz) || cur){//从尺寸小的树考虑到尺寸大的，有四种情况
		if(a.t[i] && b.t[i]){
			if(cur){
				cur=combin(cur,b.t[i]);
			}else{
				cur=combin(a.t[i],b.t[i]);
				a.t[i]=0;
			}
		}else if(a.t[i]){
			if(cur){
				cur=combin(cur,a.t[i]);
				a.t[i]=0;
			}
		}else if(b.t[i]){
			if(cur)cur=combin(cur,b.t[i]);
			else a.t[i]=b.t[i];
		}else{
			a.t[i]=cur;
			cur=0;
		}
		i++;
	}
	a.sz=i;//最后别忘了更新尺寸
}

有了$merge$操作就可以轻易实现$push$操作了，我们考虑新建一个二项堆，只有一个节点，这个节点的$val$值赋为我们要$push$的值即可，然后将这个新建的二项堆与原来的二项堆合并即可。

Bheap newnode(int x){
	val[++tot]=x;
	Bheap ans;ans.t[0]=tot,ans.sz=1,ans.top=x;
	return ans;
}
void push(Bheap &a,int x){
	Bheap b=newnode(x);
	merge(a,b);
}

最后是$pop$操作，我们先找到堆的$val$最小的根节点所在的位置，$B_{id}$是我们要找的这颗树，其根节点是$u$，那么我们将它的所有子树拆开来，根据二项堆的性质，它恰好能够拆成$B_{0\sim id-1}$，将这些树放在一个新二项堆中，然后将这个新的二项堆与原二项堆做一次合并操作即可。
代码实现的时候需要注意一些细节，详见注释：

void pop(Bheap &a){
	int id=0;
	for(int i=0;i<a.sz;++i){//先找到val最小的根节点
		if(!a.t[i])continue;
		if(val[a.t[i]]==a.top){
			id=i;
			break;
		}
	}
	Bheap b;b.sz=id;
	int u=son[a.t[id]],v=bro[u];b.top=val[u];a.t[id]=0;
	while(a.sz && !a.t[a.sz-1])a.sz--;if(a.sz)a.top=val[a.t[a.sz-1]];//更新一下a的sz和top
	for(int i=0;i<a.sz;++i)if(a.t[i])a.top=min(a.top,val[a.t[i]]);
	for(int i=id-1;i>=0;--i){//把son[u]的所有兄弟节点拆开来并一个个放到新堆b中
		b.t[i]=u;
		b.top=min(val[u],b.top);
		bro[u]=0,u=v,v=bro[v];
	}
	merge(a,b);//合并a和b即可(结果放在a中)
}

当然还可以类似左偏树一样实现减少一个指定节点$val$的操作，方法也很简单，先改变该节点的值，然后，类似二叉树我们可以让这个节点与它的父亲节点比较，如果不满足堆的性质，就与它的父亲节点交换val即可，如何寻找父亲节点呢，考虑维护一个$fa$数组，$fa[u]$代表指向$u$节点的节点，于是可以遍历$fa$，直到遇到它在树中的真父亲节点为止，由于一个父亲节点的儿子最多是$O(logn)$级别的，而一旦找到真父亲节点后，每次交换$val$都会减少当前节点深度，因此总复杂度也是$O(logn)$级别的。

这里以LuoGu P3378 【模板】堆为例给出一份参考代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
const int inf = 2147483647;
const int maxlog = 21;

int tot,bro[maxn],son[maxn],val[maxn];
struct Bheap{
	int t[maxlog]={},sz=0,top=0;
};

int combin(int u,int v){//将相同大小的树合并
	if(!u || !v)return u+v;
	if(val[u]>val[v])swap(u,v);
	bro[v]=son[u];
	son[u]=v;
	return u;
}

void merge(Bheap &a,Bheap &b){
	if(!a.sz){
		a=b;return;
	}else if(!b.sz)return;
	int i=0,cur=0;a.top=min(a.top,b.top);
	while(i<max(a.sz,b.sz) || cur){
		if(a.t[i] && b.t[i]){
			if(cur){
				cur=combin(cur,b.t[i]);
			}else{
				cur=combin(a.t[i],b.t[i]);
				a.t[i]=0;
			}
		}else if(a.t[i]){
			if(cur){
				cur=combin(cur,a.t[i]);
				a.t[i]=0;
			}
		}else if(b.t[i]){
			if(cur)cur=combin(cur,b.t[i]);
			else a.t[i]=b.t[i];
		}else{
			a.t[i]=cur;
			cur=0;
		}
		i++;
	}
	a.sz=i;
}

Bheap newnode(int x){
	val[++tot]=x;
	Bheap ans;ans.t[0]=tot,ans.sz=1,ans.top=x;
	return ans;
}
void insert(Bheap &a,int x){
	Bheap b=newnode(x);
	merge(a,b);
}
int top(Bheap &a){
	return a.top;
}
void pop(Bheap &a){
	int id=0;
	for(int i=0;i<a.sz;++i){
		if(!a.t[i])continue;
		if(val[a.t[i]]==a.top){
			id=i;
			break;
		}
	}
	Bheap b;b.sz=id;
	int u=son[a.t[id]],v=bro[u];b.top=val[u];a.t[id]=0;
	while(a.sz && !a.t[a.sz-1])a.sz--;if(a.sz)a.top=val[a.t[a.sz-1]];
	for(int i=0;i<a.sz;++i)if(a.t[i])a.top=min(a.top,val[a.t[i]]);
	for(int i=id-1;i>=0;--i){
		b.t[i]=u;
		b.top=min(val[u],b.top);
		bro[u]=0,u=v,v=bro[v];
	}
	merge(a,b);
}
int main(){
	int n;
	scanf("%d",&n);
	Bheap t;
	for(int i=1;i<=n;++i){
		int op,x;
		scanf("%d",&op);
		if(op==1){
			scanf("%d",&x);
			insert(t,x);
		}else if(op==2){
			printf("%d\n",top(t));
		}else pop(t);
	}
}

斐波拉契堆

一种常数巨大实现巨复杂的堆(貌似没有实际价值)，pairing heap其实可以完美地代替它。
所以先鸽了

STL中的堆

c++自带一些堆，首先是$priority\_queue$，对应的头文件是$queue$，声明方式是$priority\_queue<T,vector<T>,function<T>>$，$T$代表优先队列储存的数据类型，$function<T>$是一个仿函数，能够表明$T$的比较方式，$STL$中自带两个仿函数$greater<int>,less<int>$，分别代表升序降序。默认情况下的声明方式为$priority\_queue<T>q$，是大根堆。
关于$priority\_queue$的一些基本方法如下：

1. $top()$，代表取根节点$val$值
2. $empty()$，判断队列是否为空
3. $push(x)$，将$xpush$进入优先队列
4. $pop()$，$pop$操作
5. $size()$，获取队列中元素个数
   这里以LuoGu P3378 【模板】堆为例给出一份参考代码：

#include <cstdio>
#include <queue>
using namespace std;

priority_queue<int,vector<int>,greater<int>>q;

int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		int op,x;
		scanf("%d",&op);
		if(op==1){
			scanf("%d",&x);
			q.push(x);
		}else if(op==2)printf("%d\n",q.top());
		else q.pop();
	}
} 

除了$priority\_queue$，$pbds$中的优先队列更加丰富，能够实现更加复杂的功能，需要用到的头文件有$ext/pb\_ds/priority\_queue.hpp，functional$ 以及$\_\_gnu\_pbds$中的$priority\_queue$，声明方式为$priority\_queue<T,function<T>,实现方式>q$，$T$代表元素类型，$function$是仿函数，同前面的优先队列，实现方式的话主要有五种：

1. 二叉堆($binary\_heap\_tag$)
2. 二项堆($binomial\_heap\_tag$)
3. 配对堆($pairing\_heap\_tag$)
4. 斐波拉契堆($thin\_heap\_tag$)
5. $left\_child\_next\_sibling\_tag$

在使用的时候需要加上$\_\_gnu\_pbds::$，除了前面优先队列的基本操作以外$pbds$还支持$join$操作，能够实现将两个堆合并。

这里以LuoGu P3378 【模板】堆为例给出一份参考代码(不知道为什么跑得很慢)：

#include <cstdio>
#include <ext/pb_ds/priority_queue.hpp>
#include <functional>
using __gnu_pbds::priority_queue;
using namespace std;

__gnu_pbds::priority_queue<int,greater<int>,__gnu_pbds::binomial_heap_tag>q;
int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		int op,x;
		scanf("%d",&op);
		if(op==1){
			scanf("%d",&x);
			q.push(x);
		}else if(op==2)printf("%d\n",q.top());
		else q.pop();
	}
} 

堆的应用

先鸽了