二阶锥松弛在配电网最优潮流计算中的应用matlab

一、主要内容

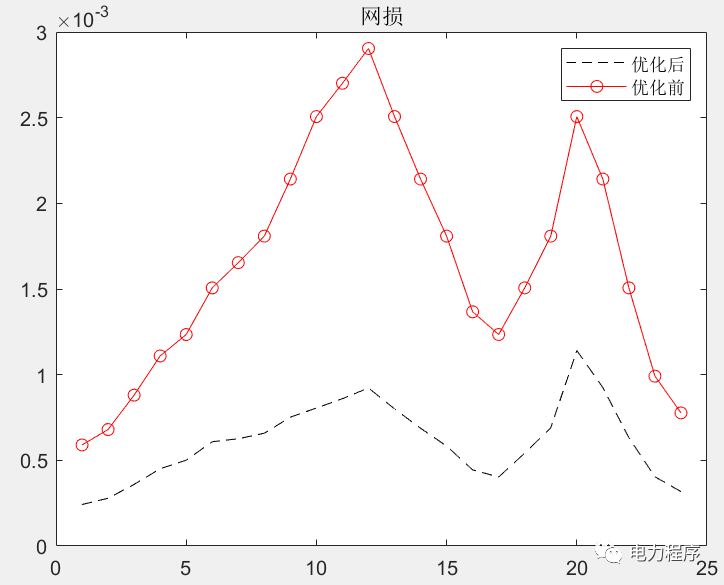
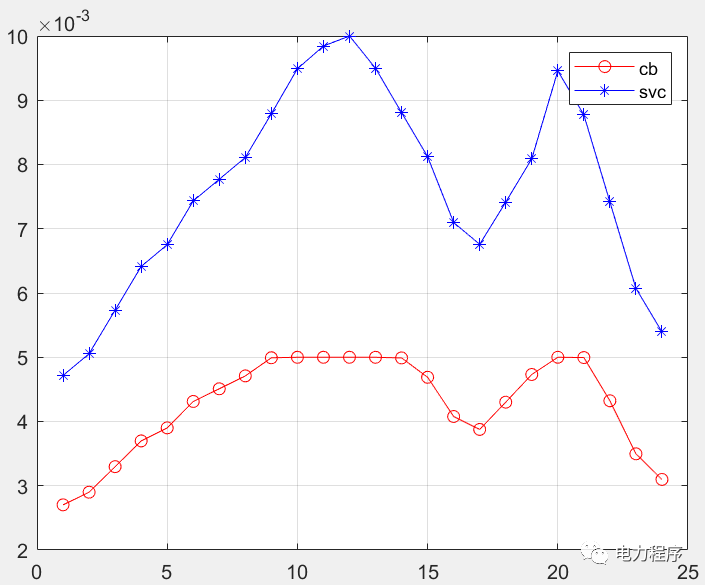
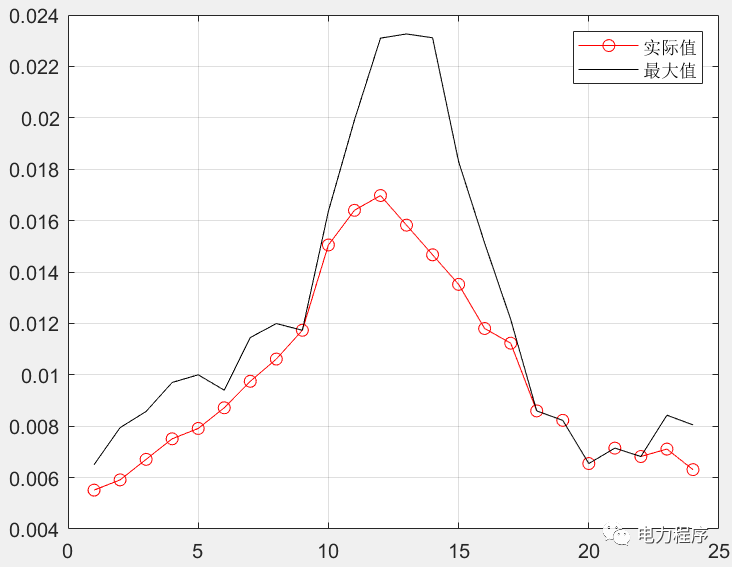
最优潮流计算是电网规划、优化运行的重要基础。首先建立了配电网全天有功损耗最小化的最优潮流计算模型；其次结合辐射型配电网潮流特点建立支路潮流约束，并考虑配电网中的可控单元，包括分布式电源和离散、连续无功补偿装置，建立其出力约束，该模型为非凸非线性模型；然后通过二阶锥松弛将该模型转化为包含整数变量的二阶锥规划模型。

​

二、部分代码

%% 1.设参mpc = IEEE33BW;pload = mpc.Pload;%节点有功负荷qload = mpc.Qload;%节点无功负荷branch = mpc.branch;branch(:,3) = branch(:,3)*100/(12.66^2);%求阻抗标幺值r = real(branch(:,3));x = imag(branch(:,3));T = 24;%时段数为24小时nb = 33;%节点数nl = 32;%支路数pw=[45.56 55.67 60.09 67.99 70.08 65.88 69.75 65.88 55.08 50.34 56.32 60.44 57.90 60.88 45.40 40.71 21.44 27.59 29.08 45.88 50.09 47.80 59.07 56.42];%光伏发电预测：pv=[0 0 0 0 0 0 5.80 10.04 15.00 35.56 45.99 56.06 58.09 55.87 45.77 36.08 35.23 18.04 15.79 0 0 0 0 0 ];​upstream = zeros(nb,nl);dnstream = zeros(nb,nl);for i = 1:nl    upstream(i,i) = 1;endfor i=[1:16,18:20,22:23,25:31]    dnstream(i,i+1) = 1;enddnstream(1,18) = 1;dnstream(2,22) = 1;dnstream(5,25) = 1;dnstream(33,1) = 1;​Vmax = [1.05*1.05*ones(nb-1,T)        1.05*1.05*ones(1,T)];Vmin = [0.95*0.95*ones(nb-1,T)        1.05*1.05*ones(1,T)];Pgmax = [zeros(nb-1,T)         ones(1,T)];Qgmax = [zeros(nb-1,T)         ones(1,T)];%% 2.设变量V = sdpvar(nb,T);%电压的平方I = sdpvar(nl,T);%电流的平方P = sdpvar(nl,T);%线路有功Q = sdpvar(nl,T);%线路无功Pg = sdpvar(nb,T);%发电机有功Qg = sdpvar(nb,T);%发电机无功gf8=sdpvar(1,T);%节点8光伏fd12=sdpvar(1,T);%节点12风电cb18=sdpvar(1,T);%节点18svc31=sdpvar(1,T);%节点31

三、程序代码

四、程序链接

程序价格1.9元，欢迎私信联系~