牛客网编程入门130题–精选(二)

本篇文章衔接博客:牛客网编程入门130–精选(一)
文章目录
题目OJ链接
1.图形相似度
描述
给出两幅相同大小的黑白图像(用0-1矩阵)表示,求它们的相似度。若两幅图像在相同位置上的像素点颜色相同,则称它们在该位置具有相同的像素点。两幅图像的相似度定义为相同像素点数占总像素点数的百分比。
输入描述:
第一行包含两个整数m和n,表示图像的行数和列数,用单个空格隔开。1≤m≤100, 1≤n≤100。之后m行,每行n个整数0或1,表示第一幅黑白图像上各像素点的颜色,相邻两个数用单个空格隔开。之后m行,每行n个整数0或1,表示第二幅黑白图像上各像素点的颜色,相邻两个数用单个空格隔开。
输出描述:
一个实数,表示相似度(以百分比的形式给出),精确到小数点后两位。
示例1
输入:
3 3 1 0 1 0 0 1 1 1 0 1 1 0 0 0 1 0 0 1输出:
44.44
?思路
相似度 = (相等的元素的个数 / 总元素)*100%
参考代码
#include <stdio.h>
int main()
{
int m = 0,n = 0;
scanf("%d %d",&m,&n);
int arr1[m][n];//变长数组
int arr2[m][n];
int count = 0;//记录相同元素的个数
for(int i = 0;i<m;++i)
{
for(int j = 0;j<n;++j)
{
scanf("%d",&arr1[i][j]);
}
}
for(int i = 0;i<m;++i)
{
for(int j = 0;j<n;++j)
{
scanf("%d",&arr2[i][j]);
if(arr1[i][j] == arr2[i][j])
{
++count;
}
}
}
printf("%.2lf\n",((double)count)/m/n*100);
return 0;
}
解释:
- 代码中采用了C99标准提出的变长数组知识点,GCC编译器支持变长数组,Visual stdio不支持
- 在输入数组2元素时,就可以跟数组1的元素进行比较了,这样可以少遍历一遍,当然时间复杂度还是一样的
2.有序数组中插入一个数
描述
有一个有序数字序列,从小到大排序,将一个新输入的数插入到序列中,保证插入新数后,序列仍然是升序。
输入描述:
共三行,
第一行输入一个整数(0≤N≤50)。
第二行输入N个升序排列的整数,输入用空格分隔的N个整数。
第三行输入想要进行插入的一个整数。
输出描述:
输出为一行,N+1个有序排列的整数。
示例1
输入:
7 5 30 40 50 60 70 90 20输出:
5 20 30 40 50 60 70 90
?思路1
“取巧”(耍赖皮),只要符合输出结果即可
遍历原来数组,如果比
num小就打印,如果比num大,就先打印num,再打印元素。这样就可以产生“视觉上”的插入数据。
参考代码
#include<stdio.h>
#include<stdbool.h>
int main()
{
int n = 0;
scanf("%d",&n);
int arr[n];
for(int i = 0;i<n;++i)
{
scanf("%d",&arr[i]);
}
int num = 0;
scanf("%d",&num);
bool flag = true;//判断是否需要插入数据
for(int i = 0;i<n;++i)
{
if(flag && num < arr[i])
{
printf("%d ",num);
flag = false;//插入完数据之后,之后就不需要再插入数据了
}
printf("%d ",arr[i]);
}
//有可能数据是最后插入的,所以咱们还需要检查一次
if(flag)
{
printf("%d",num);
}
return 0;
}
?思路2
实实在在地进行插入数据
逻辑 – 将大象放进冰箱
第一步:找到数据需要插入的位置
第二步:挪动数据,将这个位置腾出来
第三步:将数据放进该位置

挪动数据的过程
为了不在挪动的过程中将数据覆盖
方法:从后面开始挪动数据

为了更加代码可读性,可维护性,咱们使用函数实现的特定的功能
- 函数find – 查找元素位置
- 函数insert – 进行数据插入的功能
参考代码
#include <stdio.h>
int find(int* arr, int sz, int num)//这个sz是目前的元素个数
{
for (int i = 0; i<sz; ++i)
{
if (arr[i] >= num)
{
return i;
}
}
//没找到元素,就是插在最后一个位置
return sz + 1;
}
void Insert(int* arr, int* sz, int pos, int num)
{
(*sz)++;//插入数据之后,元素个数+1
int end = *sz - 1;
while (end > pos)
{
arr[end] = arr[end - 1];
--end;
}
arr[end] = num;
}
int main()
{
int n = 0;
scanf("%d", &n);
int arr[n];
for (int i = 0; i<n; ++i)
{
scanf("%d", &arr[i]);
}
int num = 0;
scanf("%d", &num);
//定位 -- 需要插入的数据的下标
int pos = find(arr, n, num);
Insert(arr, &n, pos, num);
for (int i = 0; i<n; ++i)
{
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
3.有序序列判断
描述
输入一个整数序列,判断是否是有序序列,有序,指序列中的整数从小到大排序或者从大到小排序(相同元素也视为有序)。
数据范围:3≤n≤50 序列中的值都满足 1≤val≤100
输入描述:
第一行输入一个整数N(3≤N≤50)。
第二行输入N个整数,用空格分隔N个整数。
输出描述:
输出为一行,如果序列有序输出sorted,否则输出unsorted。
示例1
输入:
5 1 6 9 22 30输出:
sorted
示例2
输入:
5 3 4 7 2 10输出:
unsorted
示例3
输入:
5 1 1 1 1 1输出:
sorted
?思路:
有序有三种情况
- 升序 — 后面的元素比前面的元素大
- 降序 — 后面的元素比前面的元素小
- 元素全部相等 – 后面的元素和前面的元素相等
我们可以将相等的情况看作升序,降序都可以
有一种思路判断无序很快:如果
既存在后面元素大于前面元素的,又存在后面元素小于前面元素的。那么该序列即为无序
其他情况则为有序。
参考代码:
#include<stdio.h>
#include<stdbool.h>//布尔类型头文件
int main()
{
//布尔类型,值只有真与假
bool assend = false;//升序
bool desend = false;//降序
int n = 0;
scanf("%d",&n);
int arr[n];
//输入数据
for(int i = 0;i < n;++i)
{
scanf("%d",&arr[i]);
}
//判断是升序状态,还是降序状态
for(int i = 1;i<n;++i)
{
if(arr[i] > arr[i-1])//后 > 前 -- 升序
{
assend = true;
}
else if(arr[i] < arr[i-1])//后 < 前 -- 降序
{
desend = true;
}
//相等既算作升序,又算作降序,不做任何处理
}
if(assend && desend)
{
printf("unsorted\n");//既是升序又是降序 -- 无序
}
else
{
printf("sorted\n");//全部相等情况也在其中
}
return 0;
}
4.矩阵初等变化
描述
KiKi有一个矩阵,他想知道经过k次行变换或列变换后得到的矩阵。请编程帮他解答。
输入描述:
第一行包含两个整数n和m,表示一个矩阵包含n行m列,用空格分隔。 (1≤n≤10,1≤m≤10)
从2到n+1行,每行输入m个整数(范围-231~231-1),用空格分隔,共输入n*m个数,表示第一个矩阵中的元素。
接下来一行输入k,表示要执行k次操作(1≤k≤5)。接下来有k行,每行包括一个字符t和两个数a和b,中间用空格格分隔,t代表需要执行的操作,当t为字符’r’时代表进行行变换,当t为字符’c’时代表进行列变换,a和b为需要互换的行或列(1≤a≤b≤n≤10,1≤a≤b≤m≤10)。
提示:当t为别的字符时不需要处理
输出描述:
输出n行m列,为矩阵交换后的结果。每个数后面有一个空格。
示例1
输入:
2 2 1 2 3 4 1 r 1 2输出:
3 4 1 2
示例2
输入:
2 2 1 3 6 8 2 c 1 2 t 1 2输出:
3 1 8 6
?思路
接收字母
- 如果是
c(col),交换矩阵两列- 如果是
r(row),交换矩阵两行
为了增加代码可读性,咱们使用函数实现特定的功能
swap – 交换两个数
swap_rc – 交换数组两行,或者两列
⚠:注意事项
- 题目要求多组输入
- 由于存在字符输入场景,需要考虑在输入字符之前清空缓冲区
参考代码
#include <stdio.h>
void Swap(int *pa,int *pb)//两数交换函数
{
int tmp = *pa;
*pa = *pb;
*pb = tmp;
}
void Swap_rc(int n,int m,int arr[n][m],char ch,int k1,int k2)//行列交换函数
{
--k1;//下标从0开始,要减1
--k2;
if('r' == ch)//row行交换
{
for(int j = 0;j<m;++j)
{
Swap(&arr[k1][j],&arr[k2][j]);
}
}
else if('c' == ch)//col列交换
{
for(int i = 0;i<n;++i)
{
Swap(&arr[i][k1],&arr[i][k2]);
}
}
}
int main()
{
int n = 0,m = 0;
scanf("%d %d",&n,&m);
int arr[n][m];
for(int i = 0;i<n;++i)
{
for(int j = 0;j<m;++j)
{
scanf("%d",&arr[i][j]);
}
}
int count = 0,k1 = 0,k2 = 0;
char ch;
scanf("%d",&count);
getchar();//吃掉缓冲区的\n
while(count--)
{
scanf("%c %d %d",&ch,&k1,&k2);
getchar();
Swap_rc(n,m,arr,ch,k1,k2);
}
for(int i = 0;i<n;++i)
{
for(int j = 0;j<m;++j)
{
printf("%d ",arr[i][j]);
}
printf("\n");
}
return 0;
}
5.杨辉三角
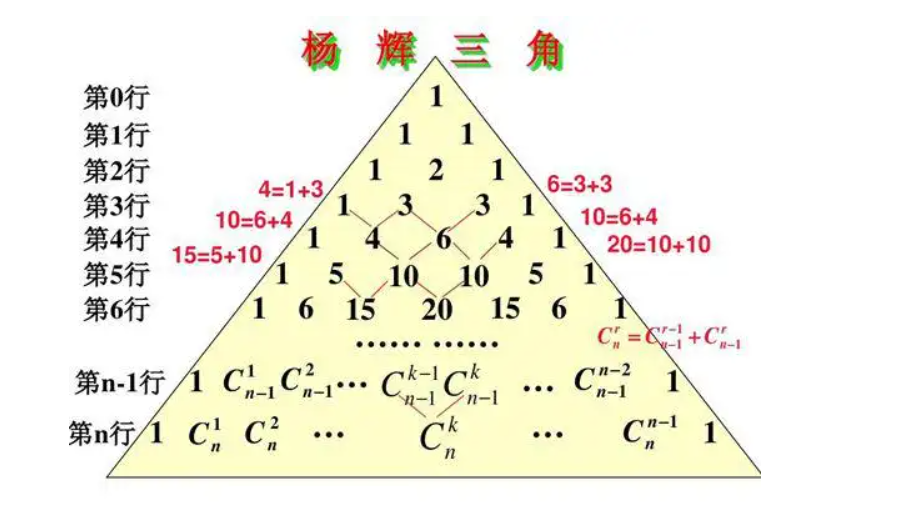
描述
KiKi知道什么叫杨辉三角之后对杨辉三角产生了浓厚的兴趣,他想知道杨辉三角的前n行,请编程帮他解答。杨辉三角,本质上是二项式(a+b)的n次方展开后各项的系数排成的三角形。其性质包括:每行的端点数为1, 一个数也为1;每个数等于它左上方和上方的两数之和。
输入描述:
第一行包含一个整数数n。 (1≤n≤30)
输出描述:
包含n行,为杨辉三角的前n行,每个数输出域宽为5。
示例1
输入:
6输出:
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1
?思路:
创建一个n行n列的二维数组
元素的有效范围:列号 <= 行号(下三角区域)
- 将第一列和主对角线的元素
- 将其他不是1的位置进行复制 == 正上方元素 + 左上方元素
- 输出
#include <stdio.h>
int main()
{
int n = 0;
scanf("%d", &n);
int arr[n][n];//变长数组
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= i; j++)
{
if (0 == j || i == j)
{
arr[i][j] = 1;
}
else
{
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
printf("%5d", arr[i][j]);
}
printf("\n");
}
return 0;
}
6.井字棋判断输赢
描述
KiKi和BoBo玩 “井”字棋。也就是在九宫格中,只要任意行、列,或者任意对角线上面出现三个连续相同的棋子,就能获胜。请根据棋盘状态,判断当前输赢。
输入描述:
三行三列的字符元素,代表棋盘状态,字符元素用空格分开,代表当前棋盘,其中元素为K代表KiKi玩家的棋子,为O表示没有棋子,为B代表BoBo玩家的棋子。
输出描述:
如果KiKi获胜,输出“KiKi wins!”;
如果BoBo获胜,输出“BoBo wins!”;
如果没有获胜,输出“No winner!”。
示例1
输入:
K O B O K B B O K输出:
KiKi wins!
?思路:
设计一个函数来判断输赢,灵活设计这个函数的返回值
- KiKi赢,返回’K’
- BoBo赢,返回’B’
- 谁都没赢返回’O’
因为
K,B,O正好是数组元素的值
判断谁赢:(三种情况)
- 一行中有三个一样的
- 一列中有三个一样的
- 主对角线三个一样的
- 副对角线三个一样的
参考代码
#include <stdio.h>
char is_win(int n,int m,char arr[n][m])
{
//1.判断行
for(int i = 0;i<n;++i)
{
for(int j = 0;j<m;++j)
{
if(arr[i][0] == arr[i][1] && arr[i][1] == arr[i][2])
{
return arr[i][0];
}
}
}
//2.判断列
for(int i = 0;i<n;++i)
{
for(int j = 0;j<m;++j)
{
if(arr[0][j] == arr[1][j] && arr[1][j] == arr[2][j])
{
return arr[0][j];
}
}
}
//3.判断主对角线
if(arr[0][0] == arr[1][1] && arr[1][1] == arr[2][2])
{
return arr[0][0];
}
//4.判断副对角线
if(arr[2][0] == arr[1][1] && arr[1][1] == arr[0][2])
{
return arr[2][0];
}
return 'O';
}
int main()
{
char arr[3][3];
for(int i = 0;i<3;++i)
{
for(int j = 0;j<3;++j)
{
scanf("%c",&arr[i][j]);
getchar();
}
}
char ret = is_win(3, 3, arr);
if (ret == 'K')
{
printf("KiKi wins!\n");
}
else if (ret == 'B')
{
printf("BoBo wins!\n");
}
else if (ret == 'O')
{
printf("No winner!\n");
}
return 0;
}
7.进制转换
描述
小乐乐在课上学习了二进制八进制与十六进制后,对进制转换产生了浓厚的兴趣。因为他的幸运数字是6,所以他想知道一个数表示为六进制后的结果。请你帮助他解决这个问题。
输入描述:
输入一个正整数n (1 ≤ n ≤ 109)
输出描述:
输出一行,为正整数n表示为六进制的结果
示例1
输入:
6输出:
10
示例2
输入:
120输出:
320
?思路
十进制下是如何取出每一位的 – 多次%10/10操作
n进制下是如何取出每一位的 – 多次%n/n操作
代码1 – 递归实现
这个跟反向输出数字逻辑类似
#include <stdio.h>
void trans_senary(int n)
{
if(n > 5)//6进制下的2位数
{
trans_senary(n / 6);//将n/6转换成六进制
printf("%d", n % 6);//再打印n%6
}
else
{
printf("%d",n);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
trans_senary(n);
printf("\n");
return 0;
}
代码2–迭代实现
取出每一位,先存在数组中,再输出。
int main()
{
int n = 0;
int arr[40] = {0};
int i = 0;
scanf("%d", &n);
while(n)
{
arr[i++] = n%6;
n/=6;
}
for(i--; i>=0; i--)
{
printf("%d", arr[i]);
}
return 0;
}
8.小乐乐定闹钟
描述
小乐乐比较懒惰,他现在想睡觉,然后再去学习。他知道现在的时刻,以及自己要睡的时长,想设定一个闹钟叫他起床学习,但是他太笨了,不知道应该把闹钟设定在哪个时刻,请你帮助他。(只考虑时和分,不考虑日期)
输入描述:
输入现在的时刻以及要睡的时长k(单位:minute),中间用空格分开。
输入格式:hour:minute k(如hour或minute的值为1,输入为1,而不是01)
(0 ≤ hour ≤ 23,0 ≤ minute ≤ 59,1 ≤ k ≤ 109)
输出描述:
对于每组输入,输出闹钟应该设定的时刻,输出格式为标准时刻表示法(即时和分都是由两位表示,位数不够用前导0补齐)。
示例1
输入:
0:0 100输出:
01:40
示例2
输入:
1:0 200输出:
04:20
?思路:
将k分钟直接加给min
- 如果min满60,进1hour
- 如果hour满24,hour变成0
⚠:注意
前导0如何输出?
#include <stdio.h>
int main()
{
int hour = 0,min = 0;
int time = 0;
while(~scanf("%d:%d",&hour,&min))
{
scanf("%d",&time);
//1.将分加进来
min += time;
//2.分转时
while(min >= 60)
{
min-=60;
hour += 1;
}
//调整时
while(hour >= 24)
{
hour -= 24;
}
//3.格式输出
printf("%02d:%02d",hour,min);
}
return 0;
}
解释:
%02d – 右对齐,设置宽度为2,如果宽度不足2补0,宽度超出忽略宽度为2的限制
格式输出扩展知识(八、十六进制格式输出)
八进制如何输出:0XXX(前面是0,八进制的标志)
十六进制如何输出:0x1234(前面是0x,十六进制的标志)
#include <stdio.h>
int main()
{
int n = 17;
//八进制
printf("%o\n", n);//按八进制输出
printf("%#o\n", n);//八进制输出 + 首位加0(八进制标志)
//十六进制
printf("%x\n", n);//按十六进制输出
printf("%#x\n", n);//十六进制输出 + 首位是0x(十六进制标志,x是小写)
printf("%#X\n", n);//十六进制输出 + 首位是0X(十六进制标志,X是大写)
return 0;
}
9.最大公因数 与 最小公倍数之和
描述
小乐乐最近在课上学习了如何求两个正整数的最大公约数与最小公倍数,但是他竟然不会求两个正整数的最大公约数与最小公倍数之和,请你帮助他解决这个问题。
输入描述:
每组输入包含两个正整数n和m。(1 ≤ n ≤ 109,1 ≤ m ≤ 109)
输出描述:
对于每组输入,输出一个正整数,为n和m的最大公约数与最小公倍数之和。
示例1
输入:
10 20输出:
30
示例2
输入:
15 20复制
输出:
65
?思路
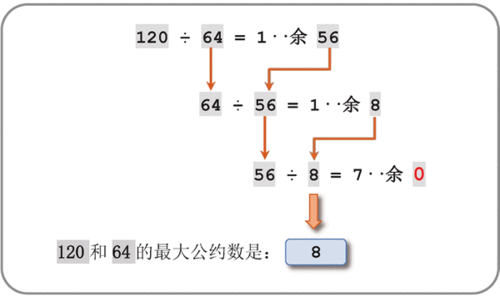
最大公因数:辗转相除法
最小公倍数:两数相乘/最大公因数即可
将最大公因数与最小公倍数相加
⚠:注意注意:两数相加可能会超出int返回,造成溢出,使用
long long类型救场
参考代码
#include <stdio.h>
long long GreComNum(int m,int n)
{
int r = 0;
do
{
r = m%n;
m = n;
n = r;
}while(r);
return m;
}
long long SmaComNum(int m,int n)
{
return (long long)m*n/GreComNum(m,n);
}
int main()
{
int m = 0;
int n = 0;
while(~scanf("%d %d",&m,&n))
{
long long ret = GreComNum(m, n);
ret += SmaComNum(m, n);
printf("%lld\n",ret);
}
return 0;
}
10.小乐乐改数字
描述
小乐乐喜欢数字,尤其喜欢0和1。他现在得到了一个数,想把每位的数变成0或1。如果某一位是奇数,就把它变成1,如果是偶数,那么就把它变成0。请你回答他最后得到的数是多少。
输入描述:
输入包含一个整数n (0 ≤ n ≤ 109)
输出描述:
输出一个整数,即小乐乐修改后得到的数字。
示例1
输入:
222222输出:
0
示例2
输入:
123输出:
101
?思路:
会取出一个数的每一位,%10/10操作
- 如果该位数是奇数,那么变成1
- 如果该位数是偶数,那么变成0
在一个数身上不好操作,不妨申请一个变量接收最终结果
参考代码:
#include <stdio.h>
#include<math.h>
int main() {
int n = 0;
int sum = 0;
int i = 0;
scanf("%d",&n);
while(n)//得到n的每一位
{
int m = n%10;
//用来接收转换之后的数字
if(m % 2 == 1)//奇数
{
m = 1;
}
else//偶数
{
m = 0;
}
n/=10;
sum += m * pow(10,i);//乘以每一位的权重再加进去
++i;
}
printf("%d\n",sum);
return 0;
}