1. 标靶平面与其图像平面的映射矩阵
角点的在世界坐标系下的坐标记为,齐次坐标为
,角点的像素坐标(转化为齐次)为
,针对小孔成像模型,空间点M与像素点m之间的射影关系为:
(1)
s为非零尺度因子,矩阵R和t为相机外部参数(相机坐标系和师姐坐标系之间的转换关系),A为相机内参。由于角点分布在2D平面上,则,则公式(1)可以写为:
(2)
(3)
其中 H为单应性矩阵,单应性在计算机视觉领域是一个非常重要的概念,它在图像校正、图像拼接、相机位姿估计、视觉SLAM等领域有非常重要的作用。文章https://blog.csdn.net/lyhbkz/article/details/82254893关于单应性矩阵讲的比较详细。
由于角点在标定板上的坐标已知,且角点的像素坐标已知,可以很容易的解出公式(3)的方程。
2. 求解相机内参矩阵。
由于R具有正交性(),其中(
,
),可得两个基本方程,
(4)
B矩阵的构造:
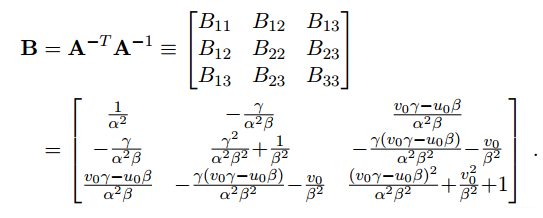
B是对称矩阵,因此可另表示为:
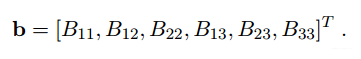
将表示为H的第i列向量,则有:
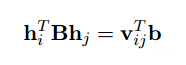
其中

公式四可以写为:
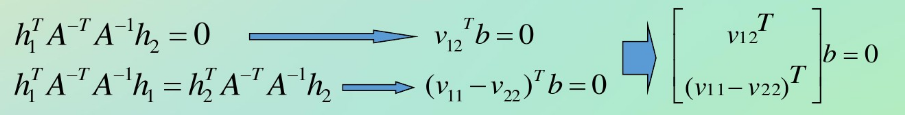
使用奇异值分解法,可以解出b矩阵。

b求解出来之后,可以利用Cholesky矩阵分解算法,求解出,

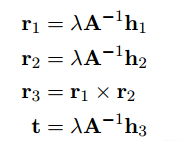
文章参考了https://blog.csdn.net/a6333230/article/details/83478064
版权声明:本文为weixin_39751162原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。