永磁同步电机矢量控制（四）——速度环 PI 参数整定(三)

一：典型II系统的开环伯德图

上一节讲了电机控制中速度环的开环传递函数，然后按照典型II系统整定。下面讲下典型II系统的整定方法。

假设系统本身的一阶惯性环中 T = 0.00004s（T = 4*Ts，Ts为采样时间0.00001s），我们先令 K = 1，τ = 0.01s，画出系统的开环传递函数的伯德图，再选择合适的中频带宽，和相位裕度来整定K和τ：

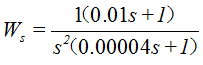
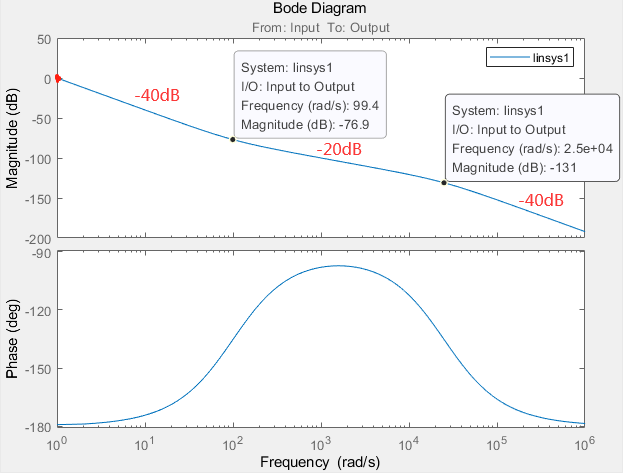
解读下开环系统的伯德图：

1. 有两个纯积分环节，幅频特性初始斜率为-40dB/dec，初始相位角度为-180°
2. 两个转折频率分为 w1 = 1/0.01 = 100rad/s, w2 = 1/0.00004 = 25000rad/s 。
3. w1 微分环节的转折频率，会导致幅频特性的曲线斜率减小-20dB/dec，相频幅值上升90°
4. w2 惯性环节的转折频率，会导致幅频特性的曲线斜率增大-20dB/dec，相频幅值下降90°
5. 在w1左侧的为低频带，在w1和w2之间的为中频带，在w2的右侧为高频带
6. 在低频带的幅相频曲线，由开环增益K和两个纯积分环节决定， 即$\frac{1}{s^2}$决定
   所以低频段的渐近线为$L_{(w)}=-40logw+20log1$,经过点$（10^0，0）$

二：开环传函中增益系数K和τ的整定

在自动控制系统里面，有两个非常关键的结论：

1: 中频带宽决定了系统的响应速度

2: 截止频率的相位裕度决定了系统的稳定性

所以参数的整定，其实是对中频带宽，和相位裕度的优化。

2.1、 设计中频带宽，计算τ

那么转速环一般需要多大的带宽呢？这个我认为是根据采样频率定的，比如采样时间为0.00001s，那么惯性环节的转折频率就是1/0.00004=25000rad/s,而lg25000 = 4.39。那么我们转速环带宽就可以设计为2.5的宽度，即lg25000 - lg x = 2.5。这样低频段的带宽为4.39 - 2.5 = 1.89（因为低频段带宽至少需要1.5的宽度） 求得 x = 80rad/s, τ = 1/x = 0.0125。这样根据中频带宽就确定了τ。

所以τ的计算公式为：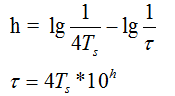

2.2、 设计相位裕度，计算K

截止频率处的相位裕度比较好确定，至少为45°
我们要取个巧，因为我们知道相频曲线的最高点，如果我们把相频曲线最高点对应的频率，设置为系统的截止频率。那么就能保证相位裕度为最大值。
因为第二个转折频率 lg25000 = 4.39(4.4)，而第一个转折频率为 lg80 = 1.9。那么中点的位置就是 1.9+2.5/2=3.15。截止频率wc = 10^(3.15) = 1412rad/s，这样截止频率的计算公式为：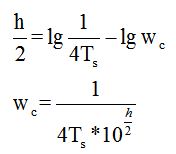

那wc和K又有什么关系呢？

所以最终K，τ参数整定的公式为：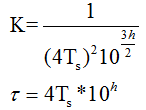

那么根据上面的公式，计算得到 K = 111140；τ = 0.0126；所以开环传递函数为：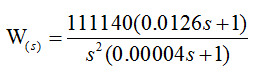

闭环传递函数框图为：

开环传函的伯德图为：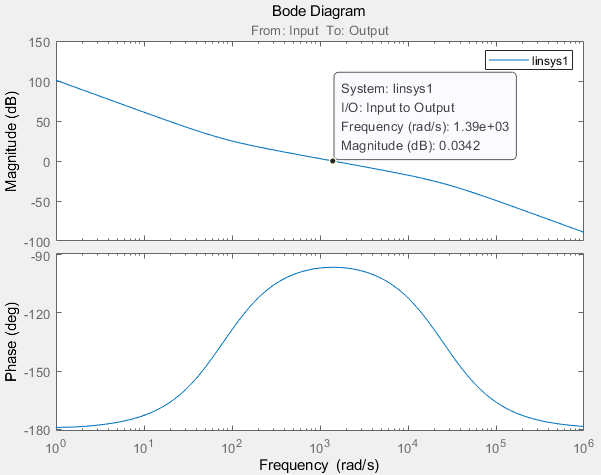

开环系统的截止频率wc = Kτ = 111140 0.0126 = 1405rad/s,和上图中的截止频率可以对应上；

闭环传函的伯德图为：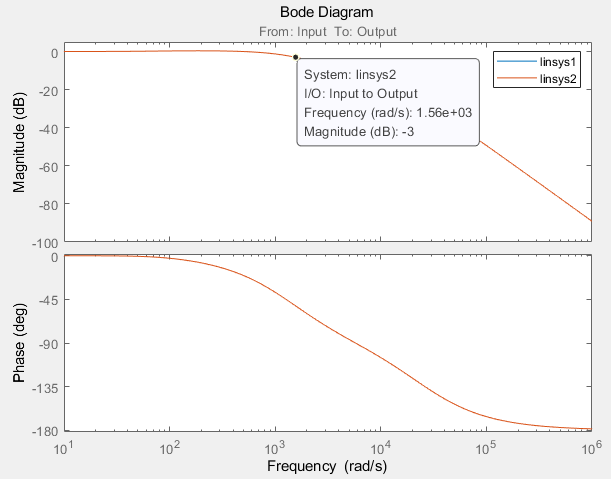

可以看出闭环系统的截止频率（wb = 1560rad/s）略大于开环系统的截止频率(wc=1405rad/s)。

三：开环增益K和微分常数τ对开环伯德图的影响

上面我们把系统的开环传函最终整定为：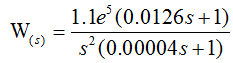

下面我们分别单独改变K和τ，然后查看开环伯德图的变换：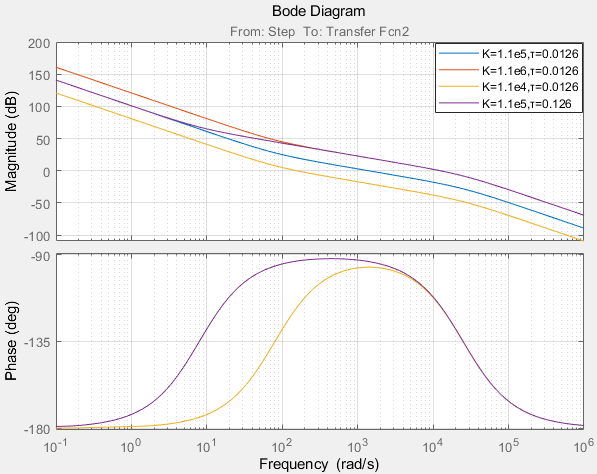

• K增大，τ不变，==>中频带宽不变， 幅频曲线向上移动，截止频率 wc 增大
• K减小，τ不变，==>中频带宽不变， 幅频曲线向下移动，截止频率 wc 减小
• τ变大，K不变，==>中频带宽变大，截止频率 wc 增大（因为斜率为 -40dB 的持续时间变短）
• τ变小，K不变，==>中频带宽变小，截止频率 wc 变小（因为斜率为 -40dB 的持续时间变长）

文章参考：https://blog.csdn.net/sy243772901/article/details/110246280