前面文章中,我们讲到,希望最终的模型在训练集上有很好的拟合(训练误差小),同时对测试集也要有较好的拟合(泛化误差小)
那么针对模型的拟合,这里引入两个概念:过拟合,欠拟合。
过拟合:是指我们在训练集上的误差较小,但在测试集上的误差较大;
欠拟合:在训练集上的效果就很差。
对于二分类数据,我们可以用下面三个图更直观的理解过拟合与欠拟合:
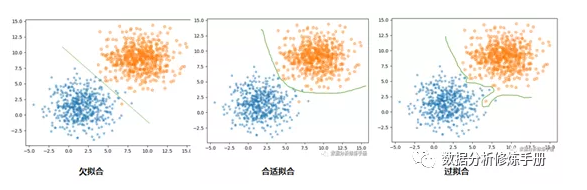
欠拟合
首先来说欠拟合,欠拟合主要是由于学习不足造成的,那么我们可以通过以下方法解决此问题
1、增加特征:增加新的特征,或者衍生特征(对特征进行变换,特征组合)
2、使用较复杂的模型,或者减少正则项
过拟合
其次讨论过拟合,为什么我们的模型会过拟合呢?这里,我总结了一下,将其原因分成两大类:
1、样本问题
样本量太少:
样本量太少可能会使得我们选取的样本不具有代表性,从而将这些样本独有的性质当作一般性质来建模,就会导致模型在测试集上效果很差;
训练集、测试集分布不一致:
对于数据集的划分没有考虑业务场景,有可能造成我们的训练、测试样本的分布不同,就会出现在训练集上效果好,在测试集上效果差的现象;
样本噪声干扰大:
如果数据的声音较大,就会导致模型拟合这些噪声,增加了模型复杂度;
2、模型问题
参数太多,模型过于复杂,对于树模型来说,比如:决策树深度较大等。
那么针对以上问题,我们要如何解决呢?
1、增加样本量:
样本量越大,过拟合的概率就越小(不过有的由于业务受限,样本量增加难以实现);
2、减少特征:
减少冗余特征;
3、加入正则项:
损失函数中加入正则项,惩罚模型的参数,降低模型的复杂度(树模型可以控制深度等);
4、集成学习:
练多个模型,将模型的平均结果作为输出,这样可以弱化每个模型的异常数据影响。
正则
这里我们重点学习一下正则化是如何降低过拟合的。
范数
我们首先了解一个范数的概念,通用公式(P范数)为: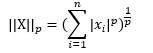
L1范数: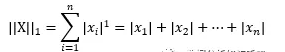
L2范数: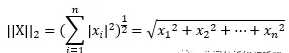
L1正则
回到我们的模型中来,就是在损失函数后面加上一个正则项来惩罚参数
L1正则:通过将特征的参数变为0,降低特征维度,来降低模型复杂度,缓解过拟合问题
假设模型只有一个参数图片,图片为不加正则项的损失函数,则加入正则项后,损失函数变为: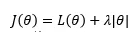
我们希望损失函数最小,因此求导如下: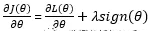
其中,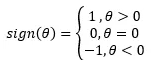
参数更新为: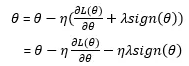

L2正则
L2正则:通过减小特征的参数,来降低模型复杂度,缓解过拟合问题
加入L2正则项后,损失函数变为: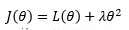
求导为: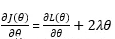
参数更新为: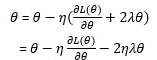
根据以上公式可以看出,L2正则化对于绝对值较大的参数惩罚较大,对绝对值较小的参数惩罚较小,当参数接近0时,基本不惩罚。

(因为越复杂的模型,越是会尝试对所有的样本进行拟合,甚至包括一些异常样本点,这就容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反映了在这个区间里的导数很大,而只有较大的参数值才能产生较大的导数。因此复杂的模型,其参数值会比较大)
图形理解
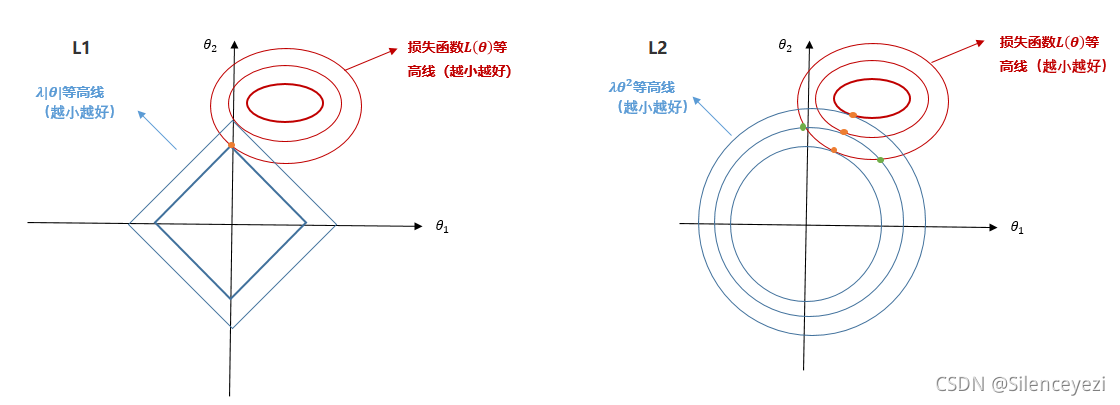
1、为什么切点处损失函数最小?
我们以L2正则为例,由等高线图我们看出:
正则项等高线的第二个蓝色圈与损失函数共有3个交点,其中橘色为切点。
我们知道深红色等高线对应的损失函数值最小,等高线越往外损失函数越大。
那么绿色交点所在等高线对应的损失函数是比切点所在等高线对应的损失函数值大的,也就是当正则项的值一定时,切点所在等高线对应的损失函数值最小
2、为什么L1正则可以得到稀疏特征,L2正则不能呢?
因为在L2正则中,两个圆一直都是相切的状态,切点永远到不了原点,也就没法让某个特征等于0,所以就没办法得到稀疏特征。
详细内容请看我公众号~
【过拟合、欠拟合】