目录
6 月 27 日,詹博华老师在SIG-元编程 技术沙龙上分享的议题《定理证明自动化中的元编程问题》,视频已经上传 B 站,欢迎小伙伴们点开观看。同时,感谢詹老师会后梳理提供了文字版,方便大家阅读。
B站链接如下:SIG-元编程技术沙龙回顾|基于元编程的可扩展访问者模式
# 定理证明 #
作为计算机科学的一个分支,定理证明研究如何通过逻辑推导的方式验证计算机程序和系统的正确性。自动定理证明关注能够完全自动证明命题的算法,例如 SAT(可满足性)和 SMT(可满足性模理论)的求解算法。交互式定理证明则是通过人和计算机的交互完成证明。在此过程中,人(用户)可以向计算机提供关于证明步骤和证明方法的更多信息,因此可以验证更复杂的定理和系统性质。一些著名的交互式定理证明的成功应用包括 seL4 操作系统微内核的验证和 C 语言编译器 CompCert 的验证。
交互式定理证明面临的一个主要挑战是对人力的要求巨大。例如,seL4 包含约 8700 行 C 代码,但其正确性证明在 Isabelle 证明辅助工具中需要超过 20 万行的证明代码。证明代码和源代码的比例大于 23:1。提高效率的一个主要途径是改善工具的自动化程度,让计算机自主完成尽可能多的证明。交互式定理证明中的证明自动化已经经过了几十年的发展,包括自动定理证明算法的使用。尽管如此,我们依然面临极大的挑战:在实际应用中,我们经常遇到对人来说相当明显的结论,但已有的证明自动化功能无法处理。
本文的目标是介绍定理证明和证明自动化所涉及的问题。我们将看到由于 “证明” 可以和 “程序” 相对应,证明自动化也可以理解为一种元编程问题。在文章的最后,我将列举一些证明自动化的挑战(从个人的观点)和目前正在进行的工作。
# 什么是证明 #
要想理解定理证明和证明自动化问题,我们首先需要理解什么是 “证明”。在交互式定理证明(以及数理逻辑)中,“证明” 是一个具有严格定义的概念,可以理解为由基本推理规则和公理组成的推导过程。为了具体说明,我们考虑一个相对简单的情景:关于等式关系的推理。等式有以下四条基本推理规则:自反性(reflexivity)、对称性(symmetry)、传递性(transitivity)和全等性(congruence)。使用数理逻辑的语言,我们可以将这些推理规则表达如下:
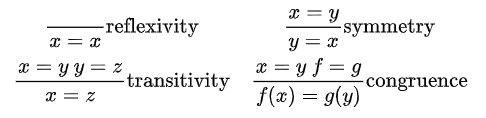
在这些规则的里,横线之上是规则的前提,横线之下是规则的结论。因此,自反性表示任何表达式 x 等于自身。对称性表示如果 x 等于 y,则 y 等于 x。传递性表示如果 x 等于 y,并且 y 等于 z,则 x 等于 z。全等性表示如果 x 等于 y,并且两个函数 f 和 g 相等,则 f(x)=g(y)。
有趣的是,我们可以将这类规则表达为程序中的函数。例如,使用 Python,这些规则可以大致书写如下:
def refl(x): # 输入x, 输出x = x
return Eq(x,x)
def symm(th): # 输入x = y, 输出y = x
if th.is_equals():
return Eq(th.rhs, th.lhs)
else:
raise Exception
def trans(th1, th2): # 输入x = y, y = z, 输出x = z
if th1.is_equals() and th2.is_equals() and th1.rhs == th2.lhs:
return Eq(th1.lhs, th2.rhs)
else:
raise Exception
def cong(th1, th2): # 输入f = g, x = y, 输出f(x) = g(y)
if th1.is_equals() and th2.is_equals():
return Eq(th1.lhs(th2.lhs), th1.rhs(th2.rhs))
else:
raise Exception这里 Eq 构建两个表达式相等的定理。is_equals 判断定理是否为等式关系。如果是,则 lhs, rhs 分别返回等式的左侧和右侧。注意后三个函数都需要输入满足一些约束,否则抛出异常。例如,传递性的应用必须保证两个输入定理都是等式,并且第一个等式的右侧和第二个等式的左侧完全一致。
脚注:在 cong 的定义中,其实还应该检查函数应用 th1.lhs(th2.lhs) 是否类型正确(如果不是,则抛出异常)。
上面的全等性规则只涉及接受一个参数的函数。我们也可以写出接受更多参数的函数的全等规则,例如:
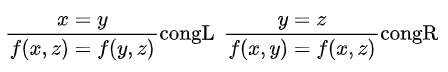
熟悉函数式语言的读者会注意到这些规则可以由自反性和一个参数函数的全等性推导得出。即使不利用这一点,我们也可以写出这两条规则对应的 Python 代码。
仅从这些推理规则还得不到什么有意思的结论。如果我们想做代数运算,我们至少还需要加法和乘法的基本规则,即交换律、结合律和分配律。这些规则是:

我们可以类似地写出相应的 Python 代码,例如:
def add_comm(x, y): # 输入x y, 输出x + y = y + x
return Eq(Plus(x, y), Plus(y, x))
def add_assoc(x, y, z): # 输入x y z, 输出(x + y) + z = x + (y + z)
return Eq(Plus(Plus(x, y), z), Plus(x, Plus(y, z)))
def distrib(x, y, z): # 输入x y z, 输出x * (y + z) = x * y + x * z
return Eq(Times(x, Plus(y, z)), Plus(Times(x, y), Times(x, z)))
# 一个简单的证明 #
下面,我们看如何使用这些规则完成一个简单的证明。我们的目标是证明以下等式关系:
![]()
我想大多数读者会认为这个等式已经足够明显,不需要任何证明。如果一定要写出证明步骤,很多人会大致回答如下:
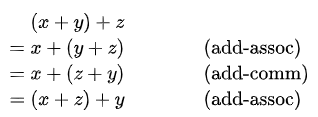
这个证明从人类的角度来说已经非常严谨了,不仅将计算拆成了三个步骤,而且标注了每个步骤使用的规则。然而,从计算机(即交互式定理证明)的角度,这个证明还缺乏一些信息,例如:
第三行:add-comm 实际上只应用于 x + (y + z) 的右侧,而不是整个表达式。如果错误地理解为将 add-comm 应用于整个表达式,那么应该得到 (y + z) + x 而不是 x + (z + y)。
第四行:add-assoc 并没有用于将括号从左边移到右边,而是反方向从右边移到左边。
我们使用了传递性规则将三步计算连接起来,但这并没有显式说明。
因此,除非计算机已经具备了一些自动证明的能力,还是无法理解上面的证明。如何写出可以让计算机理解的证明呢?受到刚才将推理规则写为程序函数的启发,我们可以尝试将证明表达为一系列函数的调用:
th1 = add_assoc(x,y,z) # (x + y) + z = x + (y + z)
th2 = add_comm(y,z) # y + z = z + y
th3 = congR("+", x, th2) # x + (y + z) = x + (z + y)
th4 = add_assoc(x,z,y) # (x + z) + y = x + (z + y)
th5 = symm(th4) # x + (z + y) = (x + z) + y
th6 = trans(th1, th3) # (x + y) + z = x + (z + y)
th7 = trans(th6, th5) # (x + y) + z = (x + z) + y经过逐步的函数调用,我们最终得到了想要的等式。其中 th1 的计算对应前面证明的第一步,th2 和 th3 对应第二步,th4 和 th5 对应第三步,th6 和 th7 使用传递性将计算连接起来。我们甚至可以将这个计算写为一行代码(为了易读添加换行):
trans(trans(
add_assoc(x,y,z),
congR("+",x,add_comm(y,z))
), symm(add_assoc(x,z,y)
))
从这个例子,我们看到一个奇妙的现象:一个命题的证明可以表达为一个产生这个命题的程序。当然,我们不能使用任何程序。否则,我们可以简单地写 Eq(0,1),然后马上证明 0=1!因此,我们需要对程序做出一些约束,可以粗略地表达为:程序只能调用一些特定的函数产生新的命题。例如,对于以上的等式推理系统,程序只能使用 refl, symm, add_comm 等函数。这些函数代表推理系统的基本推理规则和公理。当然,程序也不应允许通过任何方式修改定理的内容。这在函数式语言编程中更加容易保证(定理和其他相关对象都是不可变的)。
我们可以定义中间函数。例如,我们可以将以上证明封装为一个函数:
def swap_right(x,y,z): # 输入x y z, 输出(x + y) + z = (x + z) + y
return trans(trans(
add_assoc(x,y,z),
congR("+",x,add_comm(y,z))
), symm(add_assoc(x,z,y)
))然后在另一段程序中调用 swap_right。这种中间函数的定义对应着从基本推理规则定义更高层的推理规则或证明过程。
脚注:这也可以理解为证明并使用新的定理。然而,一般的定理证明工具都有独立的证明和使用新定理的机制。
这种“证明”和“程序”之间的对应关系可以看作 “Curry-Howard 对应” 的一种体现。真正的 Curry-Howard 对应还建立了“命题”和“类型”之间的关系,并将一个命题的证明对应于具有相应类型的程序。这种对应关系是目前大多数证明辅助工具的理论基础。由于篇幅关系,我们将不讨论相关的技术细节。
脚注:Coq 等基于依赖类型论的工具严格采用这种对应关系,而 Isabelle 等基于高阶逻辑的工具仅使用证明和程序之间的对应关系,通过声明一个定理的数据类型,并依赖编程语言的特性保证该数据类型的实例只能通过有限几个函数构造(对应于高阶逻辑的推理规则),可以保证使用这个工具得到的证明是正确的。
# 挑战和机遇 #
显然,我们在前面给出的推理系统和证明与实际应用相比过于简单。定理证明的实际应用需要更复杂的推理系统,至少添加命题逻辑符号(and, or, not, 蕴含关系)和一阶逻辑符号(all, exists)的推理。目前常用的证明辅助工具将逻辑系统进一步扩展到高阶逻辑(引入函数类型、并允许量词关于函数)和依赖类型论(类型可以设其他类型的值,例如自然数,作为参数)。同时,实际应用中我们需要完成的证明非常复杂而庞大。如果将详细的证明使用语法树的方式表达,可以占用显著比例的计算机内存空间。设计并实现能够自动产生这些复杂证明的算法也是一个巨大的挑战。读者可以思考如何自动化交换律、结合律和分配律的使用,从而给定如下命题:
![]()
能够自动生成由单个函数调用组成的证明。或者,添加指数、有理数和相应的计算规则,自动为以下等式:
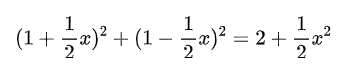
生成证明。在实际应用中,证明自动化不仅需要完成以上这些代数操作,还需要考虑不等式关系、命题逻辑和一阶逻辑符号的推理,已有定理的使用,以及如何应对庞大的搜索空间。
目前,大多数证明辅助工具提供实现证明自动化的 API,基本元素是证明策略(tactics)和策略的组合(tacticals)。然而,现有的框架面临多重挑战:
复杂命题的证明需要非常多的基本证明步骤,并且大多数步骤实际上在完成相对繁琐的计算。如何节省计算和内存消耗,但依然保证证明的正确性?
构造证明的算法多种多样,算法本身可能已经非常复杂。如何设计证明自动化的 API,允许开发者自然地表达各种复杂的算法?
目前的工具大多基于函数式语言。函数式语言提供了多方面的安全性,例如类型检查和数据不变性的保证,但使用人数相对较少。另外,一些证明自动化算法使用命令式语言表达更加自然。能否在常用的命令式语言(例如 C/C++, Java, Python)中实现证明自动化的 API,并尽可能保留函数式语言提供的安全性?
以上问题的解决可以让大规模、复杂的证明自动化算法更容易实现和使用,是交互式定理证明自动化程度提高的一个关键因素(当然,另一个关键因素是自动化算法本身的设计)。在新的证明辅助工具和证明自动化语言方面,近期已有多个研究项目,例如 Lean 交互式定理证明器,F* 程序验证工具等(大多数还是提供函数式语言的 API)。
作为相关的探索,作者本人使用 Python 实现了一个基于高阶逻辑的交互式定理证明器,名为 HolPy (Higher-order logic in Python);使用证明项、宏等概念,提供 Python 语言的证明自动化 API,并将其应用于微积分演算的自动证明生成。此外,HolPy 还用于探索新的交互式证明用户界面的设计。目前,HolPy 的设计还在不断演化中,希望在未来具有更高成熟度之后能够再做详细的介绍。
HolPy Gitee 地址:https://gitee.com/bhzhan/holpy
> 了解更多
