【二分法】找小于等于 target 的最大值 & 找大于等于 target 的最小值

一、题目描述

给你一个有序数组，和一个目标值 target ， 找到找小于等于 target 的最大值 和 大于等于 target 的最小值

示例

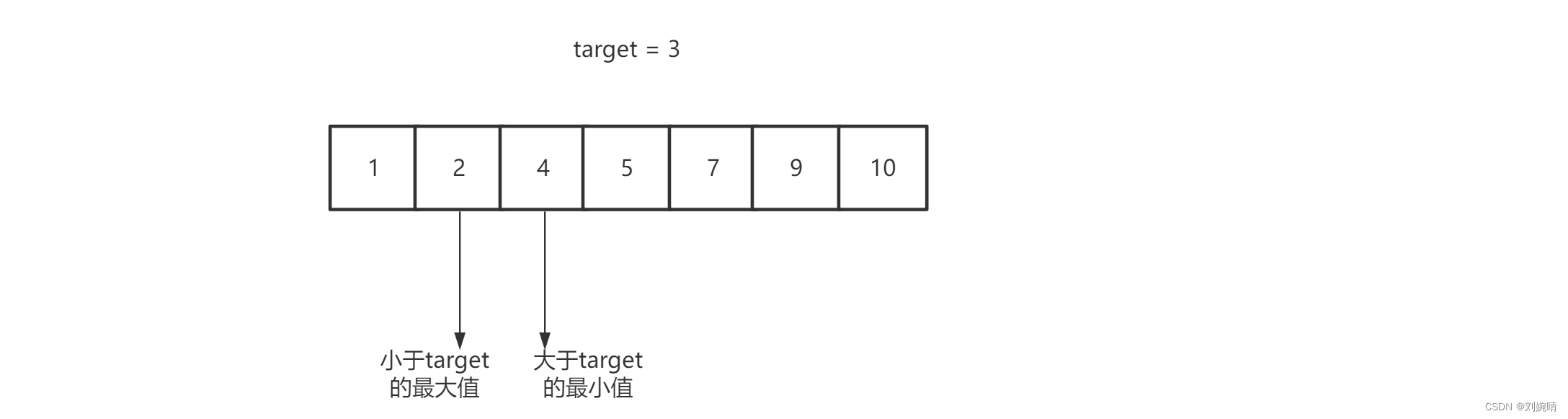
二、思路

有序数组 —— 二分查找 ，这个毫无疑问，二分查找的代码非常简单，关键在于边界条件的判断

代码：

    // 找到小于等于 target 的最大值
    public int closestNodesMax(Integer[] nums, int target){
        int left = 0;
        int right = nums.length - 1;
        while (left < right){
            int mid = left + (right - left + 1) / 2; // ***********关键点******
            if(nums[mid] == target){
                return target;
            } else if(nums[mid] > target){
                right = mid - 1;
            } else{
                left = mid;
            }
        }
        return nums[left] <= target ? nums[left] : -1;
    }

    // 找到大于等于 target 的最小值
    public int closestNodesMin(Integer[] nums, int target){
        int left = 0;
        int right = nums.length - 1;
        while (left < right){
            int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                return target;
            } else if(nums[mid] < target){
                left = mid + 1;
            } else{
                right = mid;
            }
        }
        return nums[right] >= target ? nums[right] : -1;
    }

注意点：求mid时，是否要加 1 问题

当用的数组部分为l~m不用加，为l~m-1部分就需要加1，不然有可能导致死循环。比如l=0，r=1，m=(l+r)/2=0，如果这个时候nums [m]小于target，此时l=m=0，这样的循环会陷入死循环，一直执行下去。

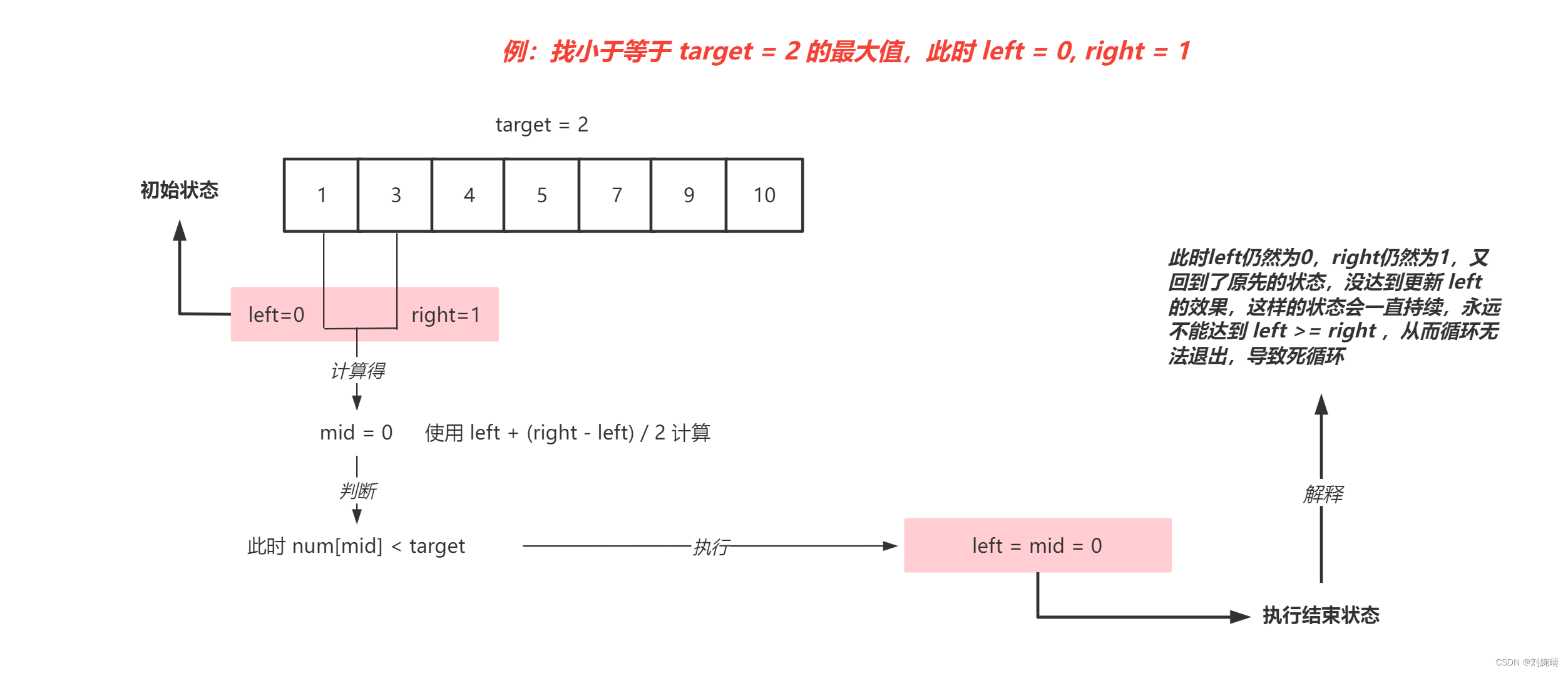
因此，我们只需要记住：

当找到小于等于 target 的最大值时，即使用的数组范围为 left ~ mid - 1 时，求 mid 时，使用 left + (right - left + 1) / 2 来避免死循环的产生