利用二分法思想求上下界（upperbound,lowerbound)

利用二分法思想求序列上下界（upperbound,lowerbound)

其实stl实现了相关函数，但是使用起来不是很方便，尤其是lowerbound返回的是指针，uperbound返回是索引。
这里的upperbound可以自己定义，例如求出第一个大于某一个数的索引。代码如下，需要注意的是实现的方式是闭区间(left=0,right=len-1)

    int findMinUp(int key,vector<int>&arr){
        int left=0;
        int right=arr.size()-1;
        while(left<=right){
            int mid=left+(right-left)/2;//avoid right+left>INT_MAX
            if(arr[mid]<=key){
                left=mid+1;
            }
            else{
                right=mid-1;
            }
        }
        return left;
    }

注意:
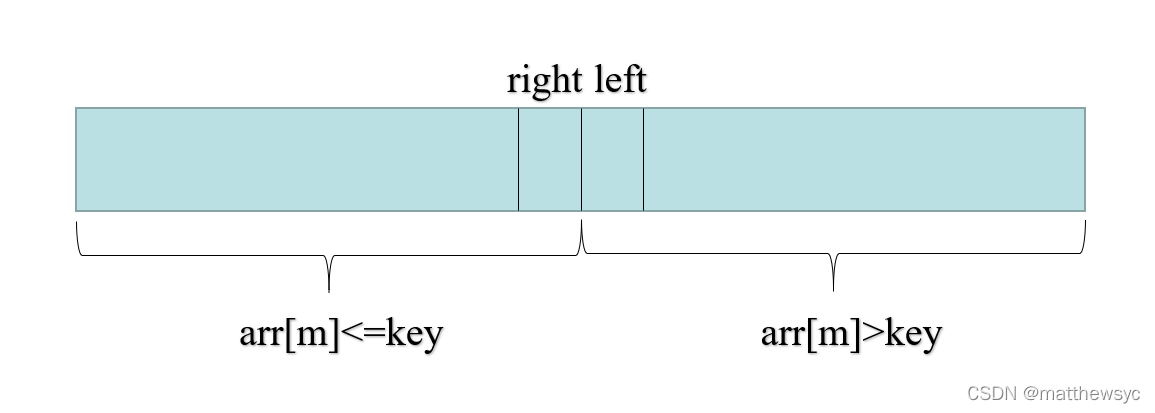
循环终止的条件是left=right+1
left左边是小于等于，right右边是大于

return right;

所以right返回的是最后一个小于等于key的索引

return left

left返回的是第一个大于key的索引。

根据以上想法，如果想找最后一个严格小于key的索引，只需要更改判断条件为arr[mid]<key