目录
1.树的概念和结构
1.1 树的概念
树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合,把它称为树是因为它看起来像一棵倒挂的树,根在上,枝叶在下。
① 根节点是一个没有前驱结点的特殊结点;
② 除根节点外,企业结点被分为M(M>0)个互不相交的集合T1,T2,T3...Tm,其中每一个集合Ti(1<=i<=m)又是一棵结构与树类型相似的子树,每棵树的根节点有且仅有一个前驱,可以有0个或多个后继;
③ 因此,树是递归定义的;
PS:树形结构中,子树之间不能有交集,即除了根节点之外,每个结点有且仅有一个直接前驱;
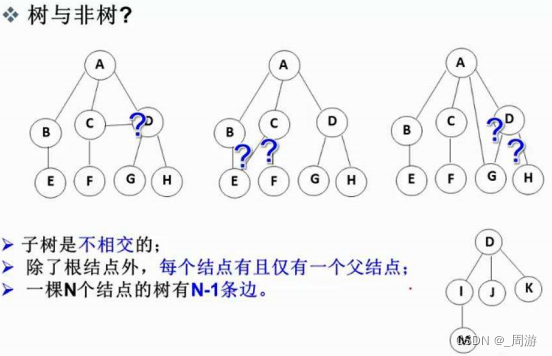
1.2 树的相关概念

(1)结点的度:一个结点含有的子树的个数,如A结点的度为6;
(2)叶结点或终端结点:度为0的结点,如H、I、P、Q、K、L、M、N;
(3)非终端结点或分支结点:度不为0的结点,如:D、E、F、G、J;
(4)双亲结点或父节点:含有子结点的结点,称该结点为其子结点的父结点,如A是B的父结点;
(5)孩子结点或子结点:一个结点含有的子树的根节点称为该结点的子结点,如B是A的子结点;
(6)兄弟结点:具有相同父结点的结点,如B和C是兄弟结点;
(7)数的度:一棵树中最大的结点的度称为数的度,如上图树的度为6;
(8)结点的层次:从根开始定义,根为第一层,根的子结点为第二层,以此类推;
(9)树的高度或深度:树中结点的最大层次,如上图树的高度或深度为4;
(10)堂兄弟结点:双亲在同一层的结点称为堂兄弟,如H和I互为堂兄弟结点;
(11)结点的祖先:从根到该结点所经分支上的所有结点,如A是所有结点的祖先;
(12)子孙:以某节点为根的子树中任一结点都成为该结点的子孙,如所有节点都是A的子孙;
(13)森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3 树的表示
树的存储相较于线性表要复杂得多,既要存储值域,也要存储结点与结点之间的关系;
树有很多种表达方式,如双亲表示法、孩子表示法、孩子双亲表示法。
最常用的是:左孩子右兄弟表示法。
图示:

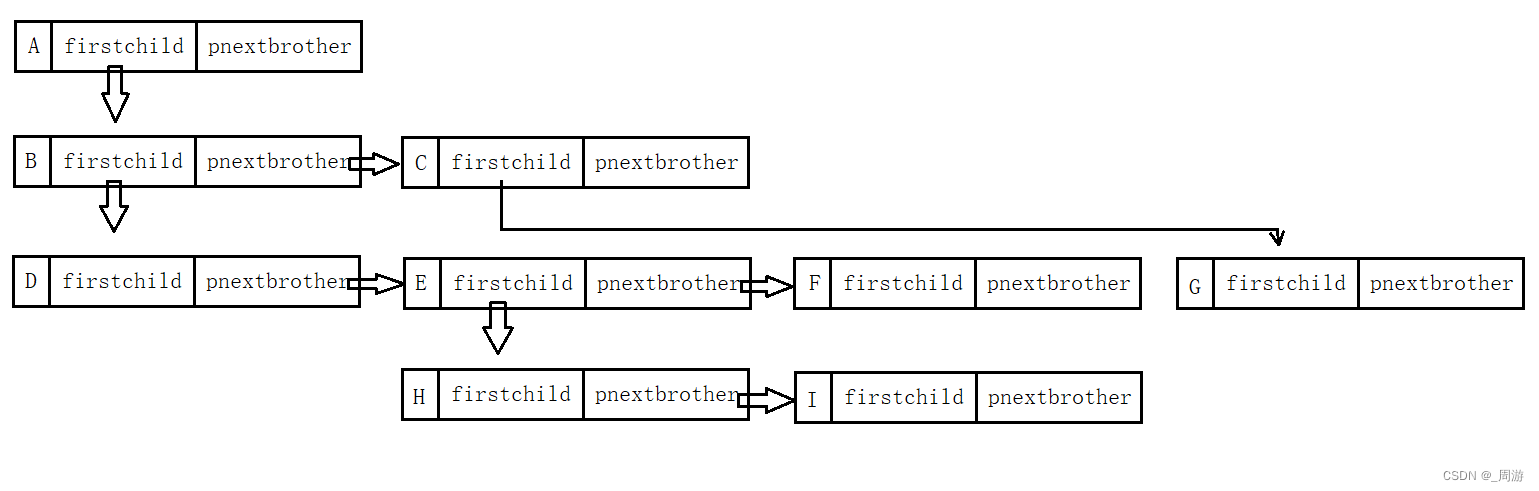
代码表示:
typedef int DataType;
struct TreeNode
{
struct TreeNode* firstchild; //指向第一个孩子结点
struct TreeNode* pnextbrother; //指向下一个兄弟结点
DataType data; //结点中的数据域
};
//注意此处的兄弟指的是亲兄弟而非堂兄弟,即此处指向的兄弟有相同的祖先1.4 树在实际中的应用—表示文件系统的目录树结构

2.二叉树的概念和结构
2.1 概念
(1)一个二叉树的结点是一个有限集合,该集合:① 或者为空 ② 有一个根节点加上两个别称为左子树和右子树的二叉树组成;
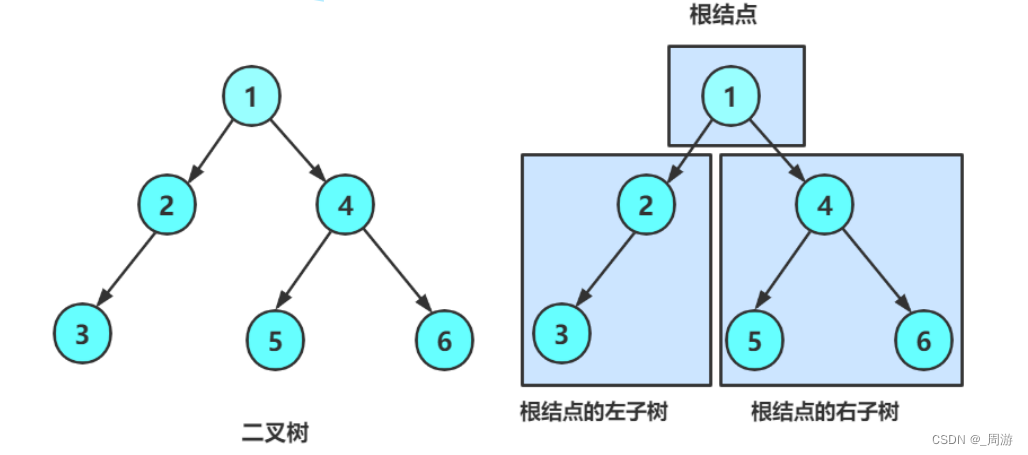
(2)特点:
① 不存在度大于2的结点;
② 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树;
(3)任意一种二叉树都是由①空树②只有根节点③只存在左子树④只存在右子树⑤左右子树均存在这五种情况复合而成;
2.2 特殊二叉树
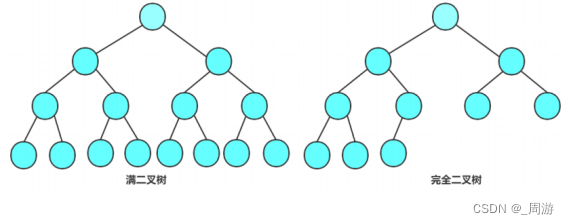
(1)满二叉树
每层节点数都是最大值的二叉树,即满足层数为k,结点总数是2^k-1的二叉树就是完全二叉树。
(2)完全二叉树
对于深度为k的二叉树,前k-1层的结点都是满的,最后一层不满但满足,存在的结点是从左向右是连续的。
2.3 二叉树的性质
(1)若规定根结点层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点;
(2)若规定根结点层数为1,则深度为h的二叉树的最大结点数是2^k-1;
(3)对任何一个二叉树,如果度为0的结点个数为n0,度为2的分支节点个数为n2,则有n0=n2+1;
(4)若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1)(以2为底);
例1:某二叉树共有399个结点,其中199个度为2的结点,则该二叉树中的叶子节点数为(B)
A.不存在这样的二叉树 B.200 C.198 D. 199
解析:根据第三条性质,叶子结点数即度为0的结点数,根据第三条性质得答案。
例2:在具有2n个结点的完全二叉树中,叶子结点个数为(A)
A.n B.n+1 C. n-1 D.n/2
解析:度为0的结点记为n0,度为1的结点记为n1,度为2的结点记为n2,根据题意有:
n0+n1+n2=2n,结合第三条性质有:n2=n0-1,代入有2*n0-1+n1=2n,对于一个完全二叉树来
说,度为1的结点只能有0个或1个,此处若n1=0,则n0为小数,故而n1只能为1,所以度为0的结
点个数为n。
例3:一个完全二叉树结点数为531个,那么这棵树的高度为(B)
A.11 B. 10 C.8 D.12
解析:高度为h的完全二叉树,结点范围是[2^(h-1),2^h-1],代入选项进行上下限计算得答案。
例4:一个具有767个结点的完全二叉树,其叶子结点个数为(B)
A.383 B. 384 C.385 D.386
解析略,同例二思路
2.4 二叉树的存储结构
二叉树的存储有两种存储方式:
(1)顺序存储结构(数组存储结构)
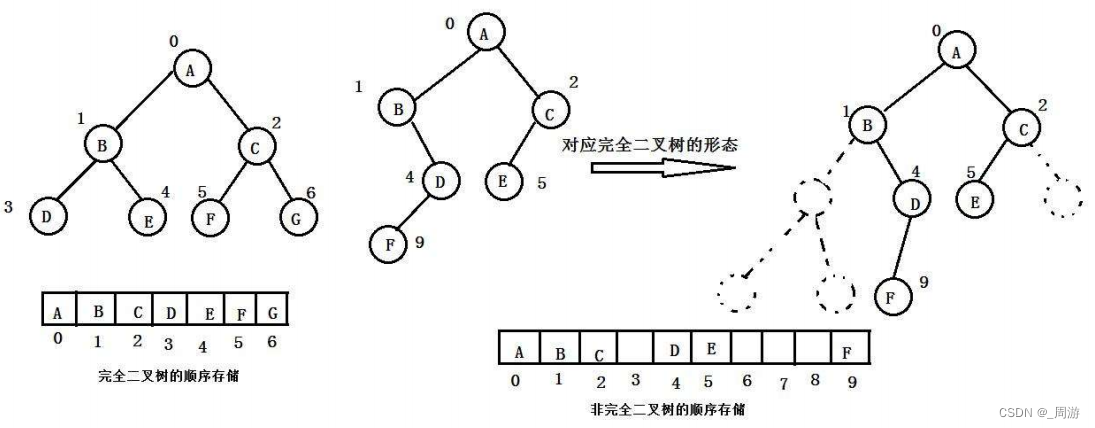
① 一般使用数组存储只适合表示完全二叉树或满二叉树,若是一般二叉树会存在很多空间浪费;
在现实使用中,只有对才会使用数组来存储;
② 二叉树的顺序存储在物理上是一个数组,在逻辑上是一个二叉树。
③ 同时顺序存储可以根据下标计算结点父子关系:
知父求子:leftchild=parent*2+1,leftchild=parent*2+2;
知子求父:(parent-1)/2;
(2)链式存储结构
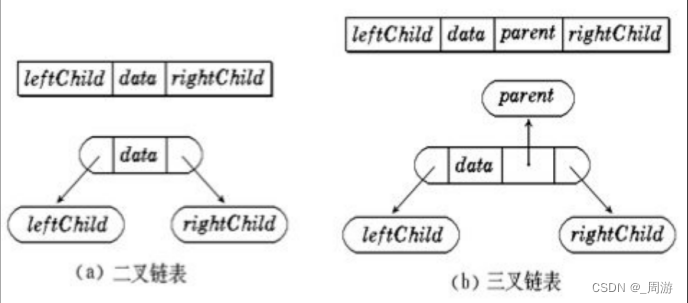
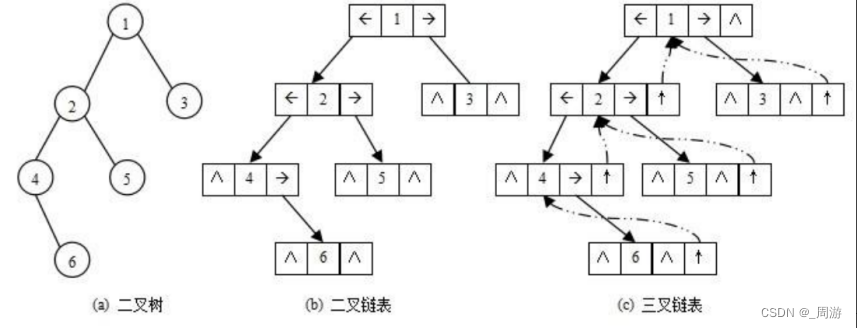
3.二叉树的顺序结构及实现
3.1 二叉树的顺序结构
一般情况下,普通二叉树不会采用顺序存储,因为存在大量的空间浪费,但是完全二叉树可以采取顺序存储的方式,此处通过堆引入二叉树顺序结构。
3.2 堆的概念及结构
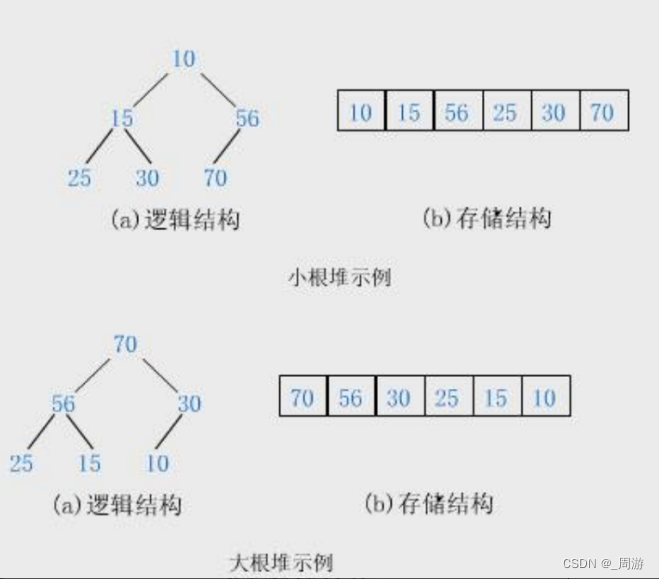
小根堆与大根堆的意义:
①、实现堆排序,时间复杂度大大降低 ②、实现TOPK
3.3 堆的实现
堆的实现是二叉树顺序存储的重难点,另开篇。
4.链式二叉树
4.1 链式二叉树的结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;4.2 二叉树的遍历
4.2.1 深度优先遍历(DFS)
深度优先遍历包括前序遍历、中序遍历与后序遍历;
前序遍历:访问根结点的操作发生在遍历其左右子树之前;(跟->左子树->右子树)
中序遍历:访问根结点的操作发生在遍历其左右子树之中;(左子树->根->右子树)
后序遍历:访问根结点的操作发生在遍历其左右子树之后;(左子树->右子树->根)

以#表示空:
前序遍历:1 2 3 # # # 4 5 # # 6 # #
中序遍历:# 3 # 2 # 1 # 5 # 4 # 6 #
后序遍历:# # 3 # 2 # # 5 # # 6 4 1
二叉树统计功能实现:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include"Queue.h"
typedef int BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
BTNode* CreatBinaryTreeNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
assert(node);
node->left = node->right = NULL;
node->data = x;
return node;
}
void TreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeDestory(root->left);
TreeDestory(root->right);
free(root);
}
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q,root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d ", front->data);
QueuePop(&q);
if (front->left)
{
QueuePush(&q,front->left);
}
if (front->right)
{
QueuePush(&q,front->right);
}
}
printf("\n");
QueueDestory(&q);
}
//判断一棵二叉树是否为完全二叉树
int BinaryTreeComplete(BTNode* root)
{
Queue p;
QueueInit(&p);
if (root)
{
QueuePush(&p,root);
}
while (!QueueEmpty(&p))
{
BTNode* front = QueueFront(&p);
QueuePop(&p);
if (front)
{
QueuePush(&p,front->left);
QueuePush(&p,front->right);
}
else
{
break;
}
}
//若空后全为空,则是完全二叉树,若空后还有非空,则不是完全二叉树;
while (!QueueEmpty(&p))
{
BTNode* front = QueueFront(&p);
QueuePop(&p);
if (front)
{
QueueDestory(&p);
return false;
}
}
QueueDestory(&p);
return true;
}
//前序遍历:
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
//中序遍历:
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
//后序遍历:
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
//统计结点数
//法一:全局定义count1计数
int count1 = 0;
void TreeSize1(BTNode* root)
{
if (root == NULL)
{
return;
}
++count1;
TreeSize1(root->left);
TreeSize1(root->right);
}
//法二:分治思路
//求左子树的结点数和右子树的结点数
int TreeSize2(BTNode* root)
{
return root == NULL ? 0 :
TreeSize2(root->left) + TreeSize2(root->right)+1;
//总结点数=左子树结点数+右子树结点数+根节点数(1)
}
//统计叶子节点数
//法一:全局定义count2计数
int count2 = 0;
void TreeLeafNode1(BTNode* root)
{
if (root == NULL)
{
return;
}
if (root->left == NULL && root->right == NULL)
{
++count2;
}
TreeLeafNode1(root->left);
TreeLeafNode1(root->right);
}
//法二:分治思路:
//求左子树的叶子结点数与右子树的叶子节点数
int TreeLeafNode2(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafNode2(root->left) + TreeLeafNode2(root->right);
}
//求第k层结点的个数
//转化为求左子树k-1层的结点数与右子树k-1层的结点数
int TreeKLevelNode(BTNode* root, int k)
{
assert(k >= 1);
if (root == NULL)
return 0;
if (k == 1)
return 1;
return TreeKLevelNode(root->left,k-1) + TreeKLevelNode(root->right,k-1);
}
//求二叉树的深度(高度)
int TreeDepth(BTNode* root)
{
if (root == NULL)
return 0;
//需要左右两子树递归结果的,采取后序遍历
int leftDepth = TreeDepth(root->left);
int rightDepth = TreeDepth(root->right);
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
//查找二叉树值为x的结点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
//不需要左右两子树递归结果的,采取前序遍历最省时
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* ret1 = TreeFind(root->left,x);
if(ret1)
return ret1;
BTNode* ret2 = TreeFind(root->right,x);
if (ret2)
return ret2;
return NULL;
}
int main()
{
BTNode* root = CreatBinaryTreeNode(1);
BTNode* node2 = CreatBinaryTreeNode(2);
BTNode* node3 = CreatBinaryTreeNode(3);
BTNode* node4 = CreatBinaryTreeNode(4);
BTNode* node5 = CreatBinaryTreeNode(5);
BTNode* node6 = CreatBinaryTreeNode(6);
root->left = node2;
root->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
printf("PreOrder: ");
PreOrder(root);
printf("\n");
printf("InOrder: ");
InOrder(root);
printf("\n");
printf("PostOrder: ");
PostOrder(root);
printf("\n");
printf("法一统计得结点数为: ");
//全局变量生命周期为整个程序,调用完一次不会销毁,计数累积,每次打印前进行置空操作
count1 = 0;
TreeSize1(root);
printf("%d \n", count1);
printf("法二统计得结点数为: ");
printf("%d \n", TreeSize2(root));
printf("法一统计得叶子结点数为: ");
count2 = 0;
TreeLeafNode1(root);
printf("%d \n", count2);
printf("法二统计得叶子结点数为: ");
printf("%d \n", TreeLeafNode2(root));
printf("第2行的结点数为: ");
printf("%d \n", TreeKLevelNode(root, 2));
printf("值为4的结点为: ");
printf("%p \n", TreeFind(root, 4));
printf("树的高度为: ");
printf("%d \n", TreeDepth(root));
printf("树层序遍历为: ");
LevelOrder(root);
printf("Complete: %d \n",BinaryTreeComplete(root));
TreeDestory(root);
root = NULL;
}4.2.2 广度优先遍历 (BFS)
(1)在二叉树的遍历中,广度优先遍历即层序遍历;
BFS的实现需要借助队列,此处队列代码实现直接衔接Queue.h与Queue.c文件
具体操作为:将Queue.h与Queue.c文件拷贝至项目文件中,再在源文件与头文件中分别添加即可。
PS:
① 互相引用:Tree.c文件中引头文件:#include"Queue.h"
在Queue.h中需使用重命名前的结构体类型进行前置声明,即在.h首添加:
struct BinaryTreeNode;② Queue Data:BFS的实现需将二叉树结点的地址存至于队列之中,定义重命名需修改为:
typedef struct BinaryTreeNode* QDataType;队列的代码详见专栏文章:【数据结构】_3.栈与队列__周游的博客-CSDN博客
代码实现:
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d ", front->data);
QueuePop(&q);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestory(&q);
}
(2)层序遍历的典型应用:判断一棵二叉树是否为完全二叉树:
代码实现:
int IsCompleteBinaryTree(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
else
{
break;
}
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
if (front)
{
QueueDestory(&q);
return false;
}
}
QueueDestory(&q);
return true;
}