A*算法路径规划之matlab实现
A*算法是一种传统的路径规划算法,相较于Dijkstra算法,其引入了启发式算子,有效的提高了路径的搜索效率。主要步骤包括:
1)设置起始点、目标点以及带障碍物的栅格地图
2)选择当前节点的可行后继节点加入到openlist中
3)从openlist中选择成本最低的节点加入closelist节点
4)重复执行步骤2和步骤3,直到当前节点到达目标点,否则地图中不存在可行路径
5)从closelist中选择从起点到终点的路径,并画图展示
所有代码如下(均可直接运行):
执行脚本,其功能是产生地图并设置起始点和目标点,通过调用astarf函数,构建closelist,并从closelist中找到路径
clear all;
clear all;
figure;
MAX_X=50;
MAX_Y=50;
dm=[1,1
1,0
0,1
-1,1
-1,-1
0,-1
-1,0
1,-1]; %八个方向
p_obstocle = 0.3;%障碍率
O = ones(MAX_X,MAX_Y)*p_obstocle;
MAP = 9999*((rand(MAX_X,MAX_Y))>O)-1;
j=0;
x_val = 1;
y_val = 1;
axis([1 MAX_X+1 1 MAX_Y+1])
set(gca,'YTick',0:1:MAX_Y);
set(gca,'XTick',0:1:MAX_X);
grid on;
hold on;
for i=1:MAX_X
for j=1:MAX_Y
if MAP(i,j) == -1
plot(i+.5,j+.5,'rx');
end
end
end
%%地图上选择起始位置
pause(1);
h=msgbox('Please Select the Vehicle initial position using the Left Mouse button');
uiwait(h,5);
if ishandle(h) == 1
delete(h);
end
xlabel('Please Select the Vehicle initial position ','Color','black');
but=0;
while (but ~= 1) %Repeat until the Left button is not clicked
[xval,yval,but]=ginput(1);
xval=floor(xval);
yval=floor(yval);
end
xStart=xval;%Starting Position
yStart=yval;%Starting Position
MAP(xval,yval) = 0;
plot(xval+.5,yval+.5,'bo');
%%地图上选择目标点
pause(1);
h=msgbox('Please Select the Target using the Left Mouse button in the space');
uiwait(h,5);
if ishandle(h) == 1
delete(h);
end
xlabel('Please Select the Target using the Left Mouse button','Color','black');
but = 0;
while (but ~= 1) %Repeat until the Left button is not clicked
[xval,yval,but]=ginput(1);
end
xval = floor(xval);
yval = floor(yval);
xTarget = xval;
yTarget = yval;
MAP(xval,yval) = 9998;
plot(xval+.5,yval+.5,'gd');
text(xval+1,yval+.5,'Target');
node = [xStart,yStart,xTarget,yTarget];
save map MAP;
save point node;
path=astarf(node,MAP);
[rnp,cnp]=size(path);
num=rnp-1;
curpoint=path(rnp,1:2);
while num>1
plot(curpoint(1,1)+.5,curpoint(1,2)+.5,'k>');
for pj=1:8
if(curpoint(1,1)+dm(pj,1)==path(num,1)&&curpoint(1,2)+dm(pj,2)==path(num,2))
if(curpoint(1,1)+dm(pj,1)==path(num-1,1)&&curpoint(1,2)+dm(pj,2)==path(num-1,2))
curpoint=path(num-1,1:2);
step=2;
else
curpoint=path(num,1:2);
step=1;
end
end
end
plot(curpoint(1,1)+.5,curpoint(1,2)+.5,'k>');
num=num-step;
end
astarf函数,其功能是不断更新openlist和closelist
function [closelist] = astarf(setpoint,map)
sp=setpoint(1,1:2);% 起始点
dp=setpoint(1,3:4);% 目标点
cp=sp; %当前点
% h=hdistance(cp,dp);% 当前点与目标点的曼哈顿距离
openlist=[cp,hdistance(cp,dp)+hdistance(cp,sp),hdistance(cp,dp)];%opne 集合
closelist=[];%clsoe 集合
existlist=[];
while judge(cp,dp)==0 %未到达目标点
openlist=sortrows(openlist,[3,4]);% 先按照g排序,再按照h排序
best=openlist(1,:); %最优子代
cp=best(1,1:2); %当前节点
fprintf("x=%d,y=%d\n",best(1,1),best(1,2));
closelist=[closelist;best]; %从openlist中选择best加入到closelist
openlist(1,:)=[]; %移除已经加入close的节点
existlist=[existlist;openlist;closelist];
openlist=[openlist;findp(existlist,best,map,sp,dp)];
end
closelist=closelist(:,1:2);
end
后继节点探索函数,探索中,不能超越地图边界,且不能探索已经在openlist和closelist中已经存在的节点
function [rp] = findp(ep,b,m,sp,dp)
%寻找周围节点
d=[1,1
1,0
0,1
-1,1
-1,-1
0,-1
-1,0
1,-1]; %八个方向
rp=[];
[r,c]=size(ep); %计算openlist行数
for di=1:8
flagf=0;
rn=r;
if(b(1,1)+d(di,1)>=1&&b(1,1)+d(di,1)<=50&&b(1,2)+d(di,2)>=1&&b(1,2)+d(di,2)<=50) % 不越出边界
if(m((b(1,1)+d(di,1)),b(1,2)+d(di,2))>0) %候选节点不是障碍物
fp=[b(1,1)+d(di,1),b(1,2)+d(di,2)];
while rn>0
if((b(1,1)+d(di,1))==ep(rn,1)&&(b(1,2)+d(di,2))==ep(rn,2)) %此点已经探索过
flagf=1;
break;
end
rn=rn-1;
end
if flagf==0
plot(b(1,1)+d(di,1)+.5,b(1,2)+d(di,2)+.5,'yh');
fp=[fp,hdistance(fp,sp)+hdistance(fp,dp),hdistance(fp,dp)];
rp=[rp;fp];
end
end
end
end
辅助函数,曼哈顿距离计算函数和相同节点判断函数
function [hd] = hdistance(p1,p2)
hd=((p2(1,1)-p1(1,1))^2+(p2(1,2)-p1(1,2))^2)^0.5;%曼哈顿距离
end
function [flagd] = judge(p1,p2)
if(p1(1,1)==p2(1,1)&&p1(1,2)==p2(1,2))
flagd=1;
else
flagd=0;
end
end
执行效果如下图所示:
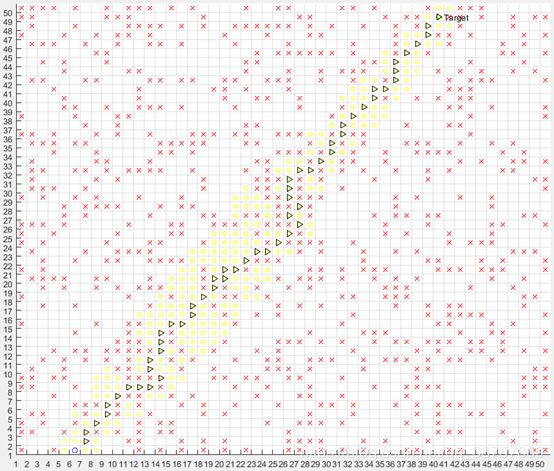
声明:此代码系作者独立撰写,能力有限,算法尚且不能保证找到最优路径,但是算法不存在错误。
注:起始点、目标点以及地图创建代码,来自MOOC网北京理工大学无人驾驶车辆课程所提供的资料包