
本章主要讨论m*n型线性方程组的解法,以前是使用消元法来解,本章将对消元法进行改进,通过引入一个新的数学工具矩阵使计算过程大为简化,主要介绍利用矩阵的初等变换解线性方程组的方法,并讨论利用矩阵来判断线性方程组无解、有唯一解或者有无限多解的充要条件.
第一节 消元法的华丽变形-高斯消元法
地点:学院大自习室;人物:小刚,小慧,小明。
讨论内容:消元法解线性方程组、矩阵的定义和初等行变换。
记录:
我:“第一章在解特殊的n*n的线性方程组的时候,我们引入了行列式的概念,但用行列式来求解太麻烦了,况且还有另外两种情况不能使用行列式来解,一是线性方程组的方程个数m多于未知数个数n,称之为超定方程组;二是相反的情况,方程个数m少于未知数个数n,称为欠定方程组,要想讨论它们的解法,还要继续研寻找新方法.”
小明:“真是路漫漫其修远兮,吾将上下而求索!”.


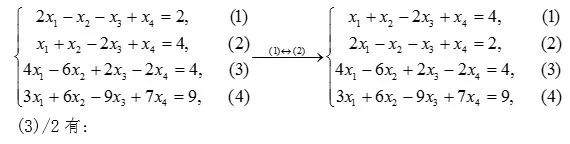

定义 同解变换
可以看到消元法的思想是用一个更易求解的线性方程组代替原线性方程组,这样会产生一个问题:上述变换后的方程组与原方程组是否同解?
我们总结一下刚才所用变换类型:
l 交换其中任意两个方程的位置,其余方程不变;
l 将其中任意一个方程乘以一个不为零的常数 ,其余方程不变;
l 将任一方程的倍数加到另一个方程上,其余方程不变。
为描述方便,将三种变换方式记为:交换、数乘和倍加。对上述三种变换进行分析发现,每一种变换都是可逆的,也就是说由原方程组得到的新方程组可以通过逆变换得到原方程组,所以原方程组的解都是新方程组的解,新方程组的解也都是原方程组的解,故变换前后的方程组是同解的,上述三种变换称为同解变换.
定义 等价
称两个线性方程组等价,如果它们的解集相同。就是说第一个方程组的解都是第二个方程组的解,第二个方程组的解也都是第一个方程组的解.
【/于老师】
小慧:“通过刚才的消元法,线性方程组解的情况可以这样判断,用消元法化到最后可能出现矛盾方程,如果有矛盾方程则线性方程组无解;也可能会出现一个或多个‘0=0’的情况,如果去掉0=0的方程所得方程组的方程个数与未知数个数相同,则可以回代得到其唯一解;如果出现自由未知量,则有无穷多个解.”
我:“对,这是判断线性方程组解的情况的方法,因为变换前后是同解的,所以消元法的实质就是用较易解的等价方程组来代替原方程组.”
1.2矩阵的相关定义
小明:“在线性方程组消元变换过程中,实际参与运算的只有系数和常数项,未知数可以不用写,这时人类的伟大的抽象思维开始发挥作用,如果将未知数去掉,剩下的将是一个二维数表,消元也就是将左下方的数字化为零的过程,当操作完成后加上未知数和相关符号就成为一个新的线性方程组,这就是一个从具体(线性方程组)到抽象(二维数据表)再到具体的思维过程,线性方程组是有灵魂的,比如方程组(1.1) 的灵魂就是:”





我:“了解了矩阵的相关概念后,下面我们的任务就是如何用矩阵这个新的数学工具来快速求解线性方程组.”
小慧:“对,根据上面用消元法求解方程组的经验,消元法的过程实际上是对方程组中的方程进行三种同解变换以得到更容易求解的等价方程组。这三种变换分别是交换、数乘和倍加.”
小明:“我来做一下对应,我们在解方程组时,只需写出其增广矩阵,对线性方程组的三种同解变换实际上就是对增广矩阵进行三种行变换!看下表:”
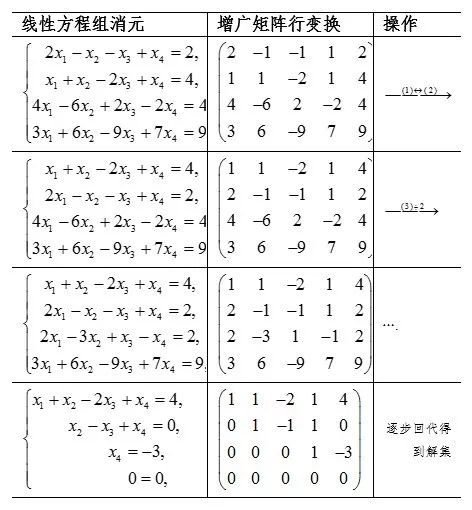
我:“很好,这样我们在解线性方程组时首先对增广矩阵进行变换,不用写出未知数,变换到最后再写出新方程组即可,所以下一步我们要好好了解一下矩阵的行变换.”



分析:先从第一行首非零元开始画阶梯形进行判断.
(a)第一二行的首非零元的列标相同,故不是行阶梯形;
(b)符合行阶梯形所有条件;
(c)零行在第一行,所以不是行阶梯形;
(d)第三、四行首非零元的列标相同,所以不是行阶梯形.
好了,我们给以上用矩阵解线性方程组的方法命名:
高斯消元法:
以上利用矩阵初等行变换求解线性方程组的方法也叫高斯消元法.
高斯消元法步骤:
引入矩阵后,求解线性方程组大大简化了,基本步骤如下:
(1) 写出方程组对应的增广矩阵B;
(2) 对矩阵进行初等行变换至行阶梯形C,此时可以判断是否有多解、唯一解或无解;
(3) 如果有解则写出C对应的线性方程组,回代求出方程组的解.
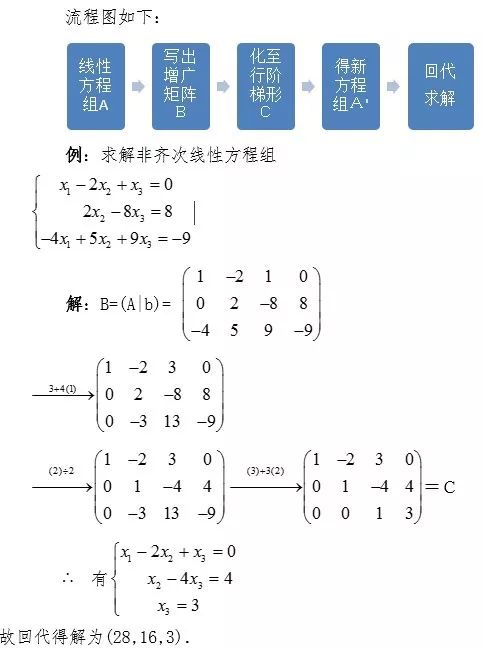



小慧:“这节课过后,我们将高中的消元法改进成了高斯消元法,在解线性方程组时,先写出线性方程组的增广矩阵,然后对矩阵进行初等行变换化至行阶梯形,最后再将矩阵对应成线性方程组,并开始回代求解。”
我:“对,消元法完成了它的华丽变形,披上了矩阵的外衣后真是变的高大上了。小刚,你怎么了?”
小刚:“睡神修普诺斯在向我招手,时间不早了,下次再讨论吧!”

原创文章,禁止转载!
点击原文查看玩转线性代数全集