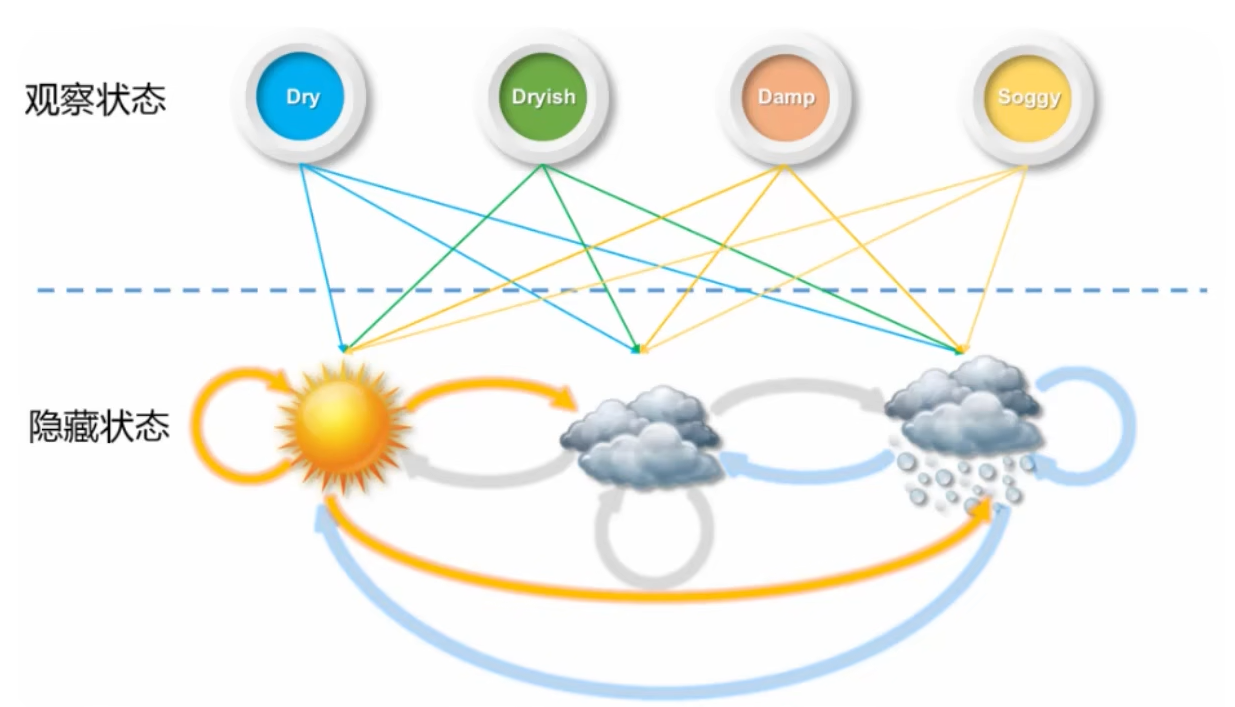
基于上一篇所讲到的 马尔可夫模型，现在难度加大了，我们观测不出天气的状态，只能通过海藻的状态来推断出天气的状态。海藻的状态有四种，分别是Dry（干燥的）、Dryish（稍干的）、Damp（潮湿的）、Soggy（湿漉漉的）。海藻的状态是可观测的，那它就是 观测状态，天气信息看不到就是 隐藏状态。

注：下图观测状态有四种状态，隐藏状态有三种，因此观测状态和隐藏状态并不是一 一对应的。

一、隐马尔可夫的定义

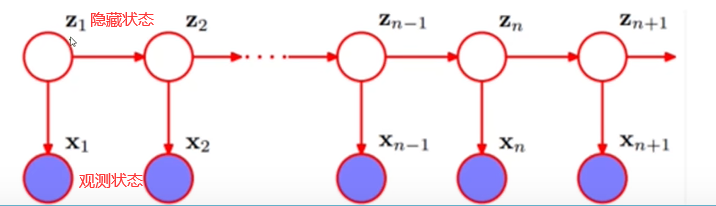
隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。

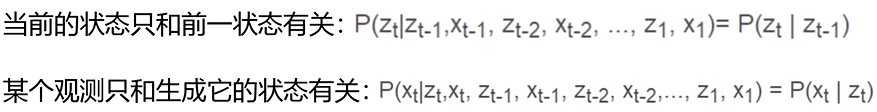
二、隐马尔可夫模型的组成

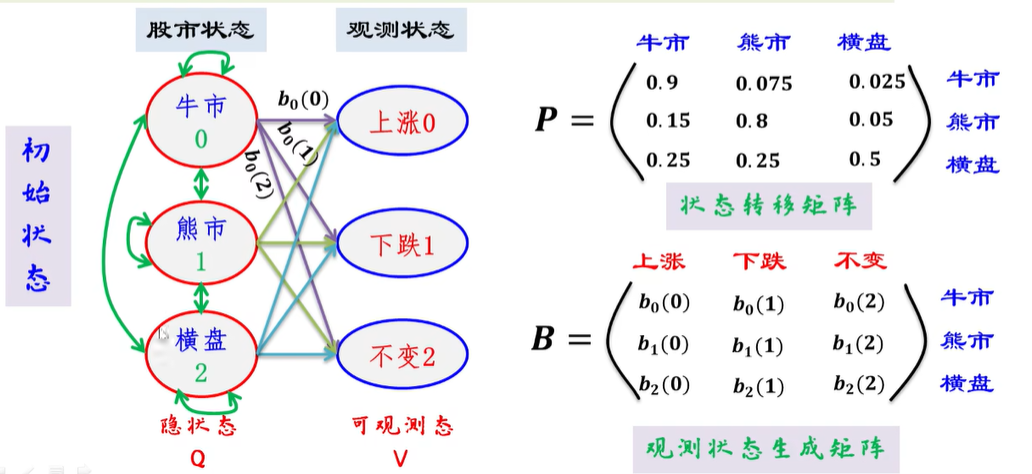
• 三个必备：初始概率（Π），隐藏状态转移概率矩阵（A），生成观测状态概率矩阵（B）。
• HMM = （Π， A， B）

三、掷骰子

我们有三种骰子，分别是六面体、四面体、以及八面体。我们将这三种骰子放进黑盒中，有放回的抽取，然后再抛这个骰子，看看它得到的是什么样的数字。经过一系列有放回的抽取和抛骰子，得到一组数字串，这组数字串就是我们的一个观测序列。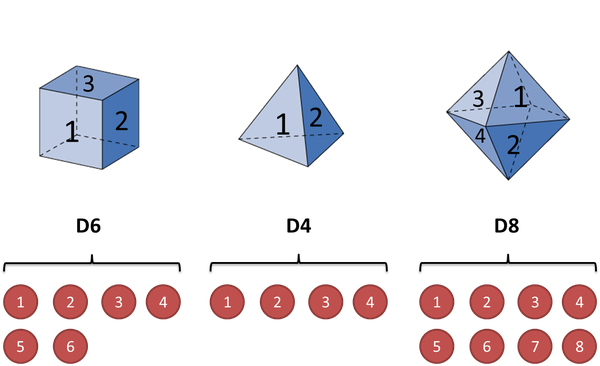

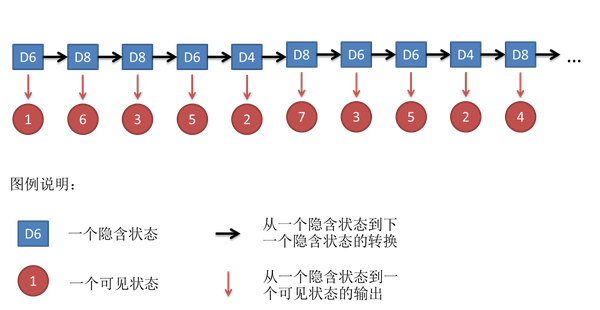
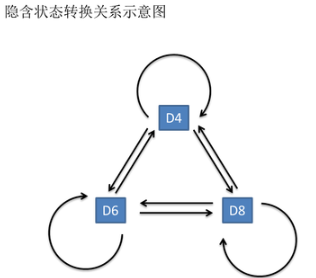
四、HMM三类问题

• 概率计算问题：给定模型λ=(Π，A，B)和观测序列O的情况下，求在模型λ=(Π，A，B)下观测序列O出现的概率P(O|λ)。（Forward-Backward算法）

• 解码问题：给定模型λ=(Π，A，B)和观测序列O的情况下，求对给定观测序列P(I | O)最大的状态序列I，即给定观测序列，求最有可能的状态序列。（Viterbi算法）

• 学习问题：观测序列O已知的情况下，求解模型λ=(Π，A，B)参数，使得在该模型下观测序列概率P(O|λ)最大。（极大似然估计算法）

五、前向算法

• 前向概率：给定马尔可夫模型 λ，定义到 t 时刻部分观测序列为o1，o2…ot且状态为qt的概率为前向概率。
  
  

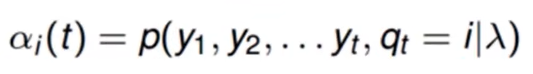
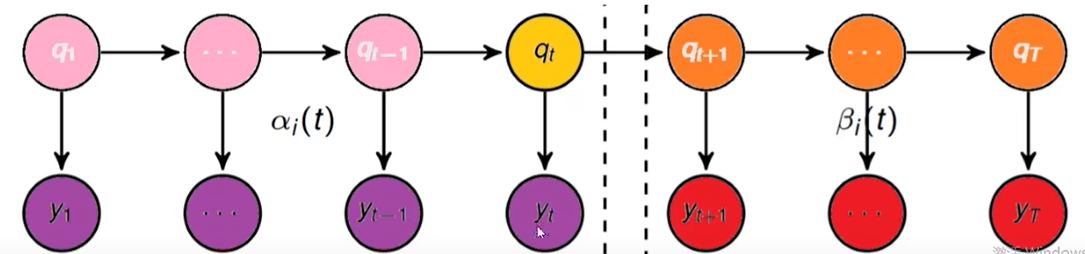
六、前向算法求解案例

求解（Π，A，B）