视觉SLAM十四讲学习5 位姿估计(5)PNP方法,BA
前言
本篇记录PnP中的BA光束平差法。
重投影误差
对于3D-2D的位姿估计,还可以通过最小化重投影误差实现。重投影误差公式如下:
∑ ∣ ∣ e ∣ ∣ = ∑ ∣ ∣ x − 1 s K T P ∣ ∣ P = [ X , Y , Z ] \sum ||e||=\sum ||x-\frac{1}{s}KTP|| \\ P=[X,Y,Z]∑∣∣e∣∣=∑∣∣x−s1KTP∣∣P=[X,Y,Z]
一般,对于向量范数的最小化,可以转化为最小二乘问题:
arg min T ∑ 1 2 ∣ ∣ e ∣ ∣ 2 = arg min T ∑ 1 2 ∣ ∣ x − 1 Z K T P ∣ ∣ 2 \argmin_{T} \sum \frac {1}{2} ||e||^2=\argmin_{T} \sum \frac{1}{2}||x-\frac{1}{Z}KTP||^2Targmin∑21∣∣e∣∣2=Targmin∑21∣∣x−Z1KTP∣∣2
对于非线性最小二乘问题,可以转化为非线性优化问题,通过牛顿法,拟牛顿法,共轭梯度等方法解决。这里使用高斯牛顿法求解:
Δ = − ( J T J ) − 1 J T f \Delta =-(J^TJ)^{-1}J^TfΔ=−(JTJ)−1JTf
那么,现在BA的问题就转变为求梯度J T = ∇ e J^T =\nabla eJT=∇e的问题。
重投影误差关于位姿的梯度
设, P ′ = T P [ 1 : 3 ] = R P + t = [ X ′ , Y ′ , Z ′ ] , x = [ u , v ] T , s = Z ′ , P'=TP_{[1:3]}=RP+t=[X',Y',Z'],x=[u,v]^T,s=Z',P′=TP[1:3]=RP+t=[X′,Y′,Z′],x=[u,v]T,s=Z′,则:
e = x − 1 s K P ′ ∇ e = ∂ e ∂ P ′ ∂ P ′ ∂ T e=x-\frac{1}{s}KP' \\ \quad \\ \nabla e=\frac{\partial e}{\partial P'} \frac{\partial P'}{\partial T}e=x−s1KP′∇e=∂P′∂e∂T∂P′
梯度的前一项可以根据相机模型计算:
e = x − [ 1 Z ′ f x 0 1 Z ′ c x 0 1 Z ′ f y 1 Z ′ c y ] [ X ′ , Y ′ , Z ′ ] T [ u v ] − [ 1 Z ′ f x X ′ + c x 1 Z ′ f y Y ′ + c y ] ∂ e ∂ P ′ = − [ 1 Z ′ f x 0 0 1 Z ′ f y − 1 Z ′ 2 f x X ′ − 1 Z ′ 2 f y Y ′ ] T e = x - \begin{bmatrix} \frac{1}{Z'}f_x & 0 & \frac{1}{Z'}c_x \\ 0 & \frac{1}{Z'}f_y & \frac{1}{Z'}c_y \\ \end{bmatrix}[X',Y',Z']^T \\ \quad \\ \begin{bmatrix}u \\ v \end{bmatrix} - \begin{bmatrix} \frac{1}{Z'}f_xX' + c_x \\ \frac{1}{Z'}f_yY' + c_y \\ \end{bmatrix} \\ \quad \\ \frac {\partial e}{\partial P'} = -\begin{bmatrix} \frac{1}{Z'}f_x & 0 \\ 0 & \frac{1}{Z'}f_y \\ -\frac{1}{Z'^2}f_xX' & -\frac{1}{Z'^2}f_yY' \\ \end{bmatrix}^T \\e=x−[Z′1fx00Z′1fyZ′1cxZ′1cy][X′,Y′,Z′]T[uv]−[Z′1fxX′+cxZ′1fyY′+cy]∂P′∂e=−⎣⎡Z′1fx0−Z′21fxX′0Z′1fy−Z′21fyY′⎦⎤T
梯度的后一项,由于变换矩阵T TT不好求导,因此可以借助李代数的左乘扰动模型求导:
∂ P ′ ∂ T = ∂ ( ( T P ) [ 1 : 3 ] ) ∂ T = ( ∂ ( e δ ∧ P ) ∂ Δ δ ) [ 1 : 3 ] = [ I − ( R P + t ) ∧ ] = [ I − P ′ ∧ ] \frac{\partial P'}{\partial T}=\frac{\partial ((TP)_{[1:3]})}{\partial T} \\ \quad \\ = (\frac {\partial (e^{\delta^\land}P)}{\partial \Delta\delta})_{[1:3]} \\ \quad \\ = \begin{bmatrix} I & -(RP+t)^\land \end{bmatrix} \\ \quad \\ = \begin{bmatrix} I & -P'^\land \end{bmatrix} \\∂T∂P′=∂T∂((TP)[1:3])=(∂Δδ∂(eδ∧P))[1:3]=[I−(RP+t)∧]=[I−P′∧]
于是,总梯度就出来了:
∇ e = − [ 1 Z ′ f x 0 0 1 Z ′ f y − 1 Z ′ 2 f x X ′ − 1 Z ′ 2 f y Y ′ ] T [ I − P ′ ∧ ] = − [ 1 Z ′ f x 0 − 1 Z ′ 2 f x X ′ 0 1 Z ′ f y − 1 Z ′ 2 f y Y ′ ] [ I − P ′ ∧ ] = − [ A B ] [ I − P ′ ∧ ] = − [ A − A P ′ ∧ B − B P ′ ∧ ] \nabla e = -\begin{bmatrix} \frac{1}{Z'}f_x & 0 \\ 0 & \frac{1}{Z'}f_y \\ -\frac{1}{Z'^2}f_xX' & -\frac{1}{Z'^2}f_yY' \\ \end{bmatrix}^T \begin{bmatrix} I & -P'^\land \end{bmatrix} \\ \quad \\ = -\begin{bmatrix} \frac{1}{Z'}f_x & 0 & -\frac{1}{Z'^2}f_xX' \\ 0 & \frac{1}{Z'}f_y & -\frac{1}{Z'^2}f_yY' \\ \end{bmatrix} \begin{bmatrix} I & -P'^\land \end{bmatrix} \\ \quad \\ = -\begin{bmatrix} A \\ B \end{bmatrix} \begin{bmatrix} I & -P'^\land \end{bmatrix} = -\begin{bmatrix} A & -AP'^\land \\ B & -BP'^\land \end{bmatrix} \\ \quad \\∇e=−⎣⎡Z′1fx0−Z′21fxX′0Z′1fy−Z′21fyY′⎦⎤T[I−P′∧]=−[Z′1fx00Z′1fy−Z′21fxX′−Z′21fyY′][I−P′∧]=−[AB][I−P′∧]=−[AB−AP′∧−BP′∧]
展开后长这样: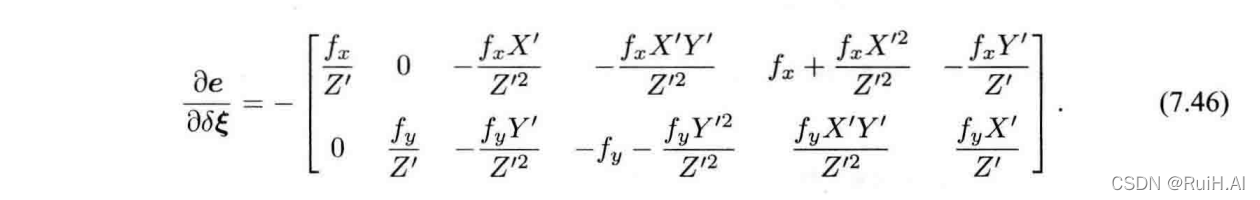
这样就得到了关于位姿的梯度。
重投影误差关于点的梯度
BA不仅可以用于位姿的优化,也可以对点进行优化,此时的重投影误差最小二乘变成了:
arg min T , P ∑ 1 2 ∣ ∣ e ∣ ∣ 2 \argmin_{T,P} \sum \frac {1}{2} ||e||^2T,Pargmin∑21∣∣e∣∣2
关于点的梯度:
∇ e = ∂ e ∂ P ′ ∂ P ′ ∂ P = ∂ e ∂ P ′ ∂ ( R P + t ) ∂ P = − [ 1 Z ′ f x 0 − 1 Z ′ 2 f x X ′ 0 1 Z ′ f y − 1 Z ′ 2 f y Y ′ ] R \nabla e = \frac {\partial e}{\partial P'} \frac {\partial P'}{\partial P} = \frac {\partial e}{\partial P'} \frac {\partial (RP+t)}{\partial P} \\ \quad \\ = -\begin{bmatrix} \frac{1}{Z'}f_x & 0 & -\frac{1}{Z'^2}f_xX' \\ 0 & \frac{1}{Z'}f_y & -\frac{1}{Z'^2}f_yY' \\ \end{bmatrix} R∇e=∂P′∂e∂P∂P′=∂P′∂e∂P∂(RP+t)=−[Z′1fx00Z′1fy−Z′21fxX′−Z′21fyY′]R
BA
得到上面这两个梯度之后,代入高斯牛顿法的增量迭代公式,直到达成收敛条件:
∇ e = J T Δ δ = − ( J T J ) − 1 J T f T ′ = e Δ δ T u n t i l ∣ ∣ Δ δ ∣ ∣ < α o r ∣ ∣ ∇ e ∣ ∣ < β \nabla e = J^T \\ \Delta \delta =-(J^TJ)^{-1}J^Tf \\ T' = e^{\Delta \delta} T \\ \quad \\ until \quad ||\Delta \delta||<\alpha \quad or \quad ||\nabla e||<\beta∇e=JTΔδ=−(JTJ)−1JTfT′=eΔδTuntil∣∣Δδ∣∣<αor∣∣∇e∣∣<β
这就是BA的基本流程。
后记
下篇ICP,然后是光流跟踪和直接法。前端结束后,学习Ceres和g2o