高斯分布又叫正态分布,是统计学中最重要的连续概率分布。研究表明,在物理科学和经济学中,大量数据的分布通常是服从高斯分布,所以当我们对数据潜在分布模式不清楚时,可以优先用高斯分布近似或精确描述。高斯分布分为一维高斯分布和多维高斯分布。
一维高斯分布
假设一维随机变量X服从高斯分布如下:
它的概率密度函数见公式为:
以上高斯分布曲线取决于两个因素:均值和标准差。分布的均值决定了图形中心的位置,标准差决定了图像的高度和宽度。标准差大时,曲线呈现出“矮胖”,标准差小时,曲线呈现出“高瘦”。因此通过改变均值和标准差,根据其概率密度函数得到不同的高斯分布,见下图。,
时,就得到了标准高斯分布。

高斯分布(一维)具有以下性质:
- 曲线下的总面积为1。
- 随机变量X等于任何特定值的概率为0。
- X大于a的概率等于以a为界到正无穷大的曲线下的面积。
- X小于a的概率等于从负无穷大到以a为界的曲线下的面积。
- 大约0.68的曲线下面积落在平均值的 1 个标准偏差内;大约0.95的曲线下面积落在平均值的 2 个标准差内;大约0.997的曲线下面积落在平均值的 3 个标准差内。
多维高斯分布
多维高斯分布其变量为n维变量,每个变量之间可能会存在关系,为了描述这种关系,我们引入了协方差矩阵。多维变量
的联合概率密度函数为下式:
其中:
- d:变量维度。对于二维高斯分布,有d=2。
:各位变量的均值。
:协方差矩阵,描述各维变量之间的相关度。对于二维高斯分布,有:
后文主要分析均值和协方差矩阵对二维高斯分布的影响。
在情况下,见二维高斯分布图,在XY坐标轴上形成的投影(等高图)见下图:
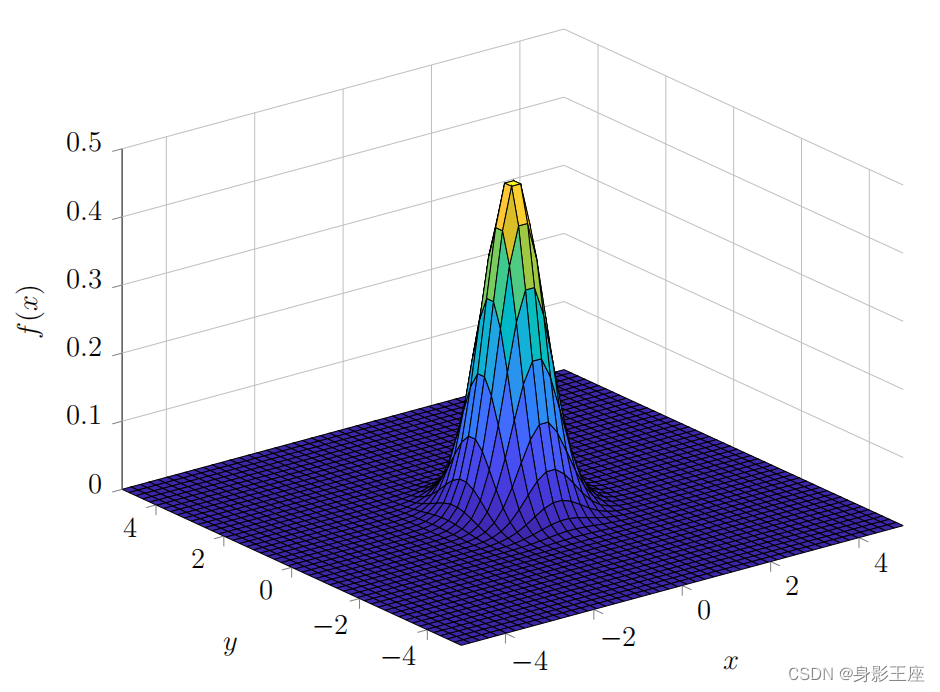
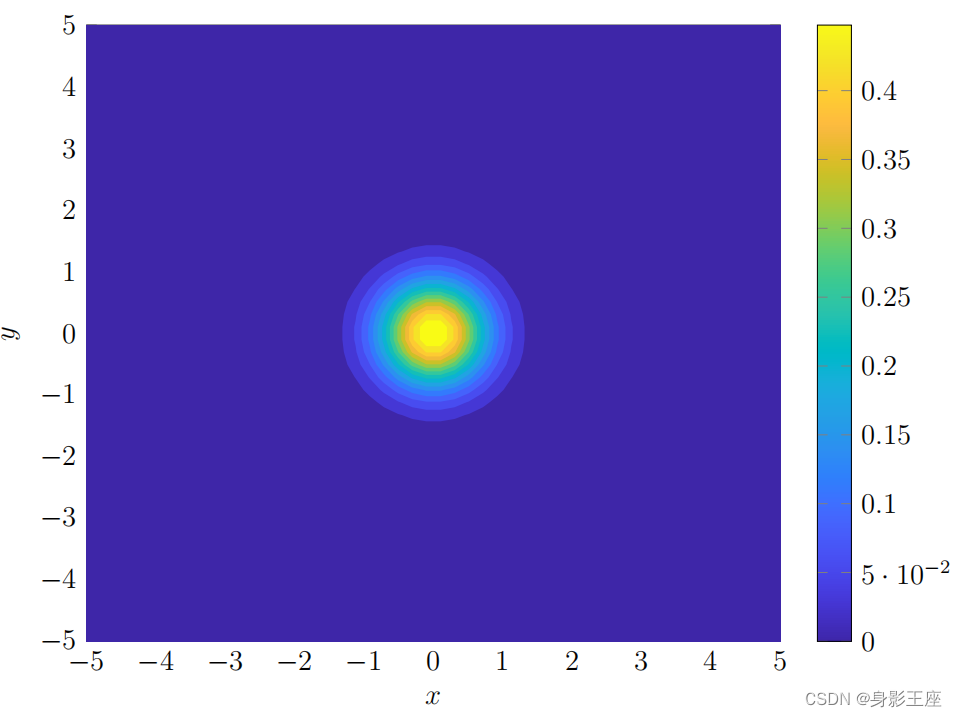
在情况下,见二维高斯分布图,在XY坐标轴上形成的投影(等高图)见下图:
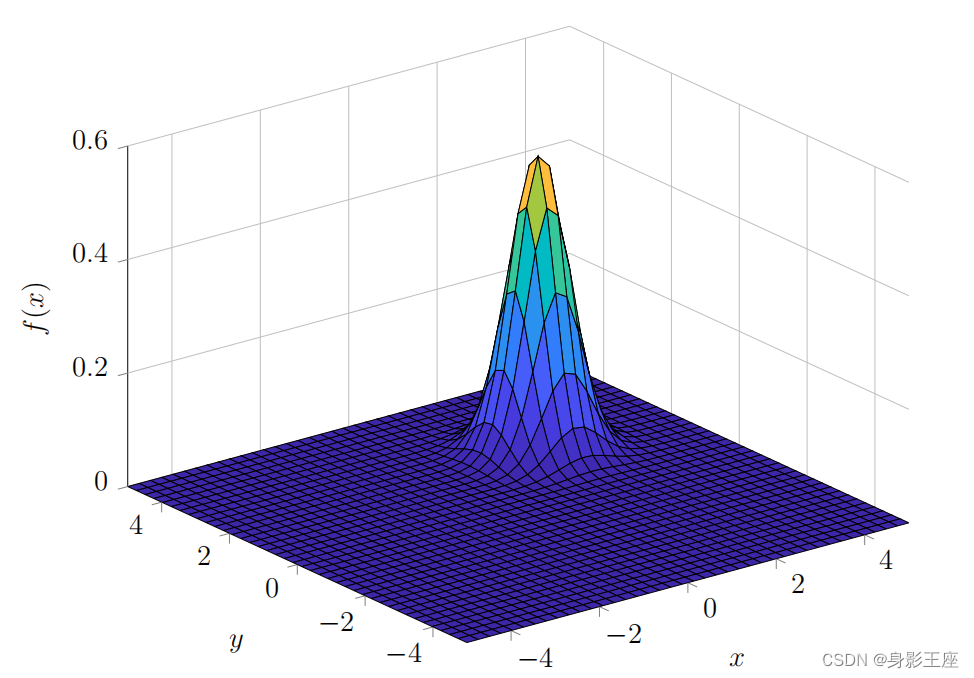
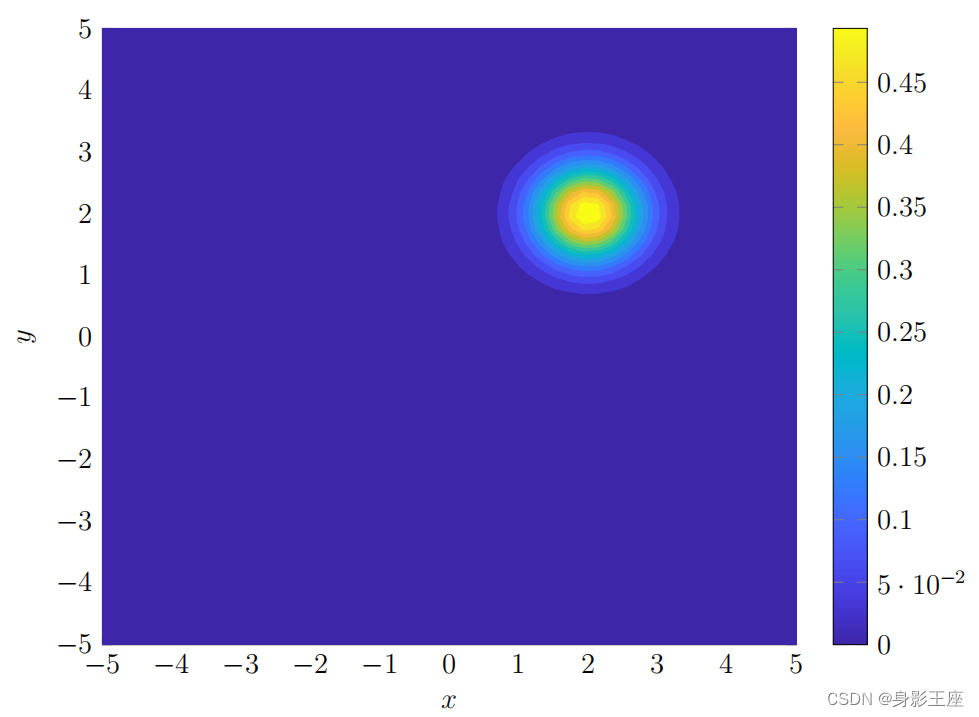
在情况下,见二维高斯分布图,在XY坐标轴上形成的投影(等高图)见下图:

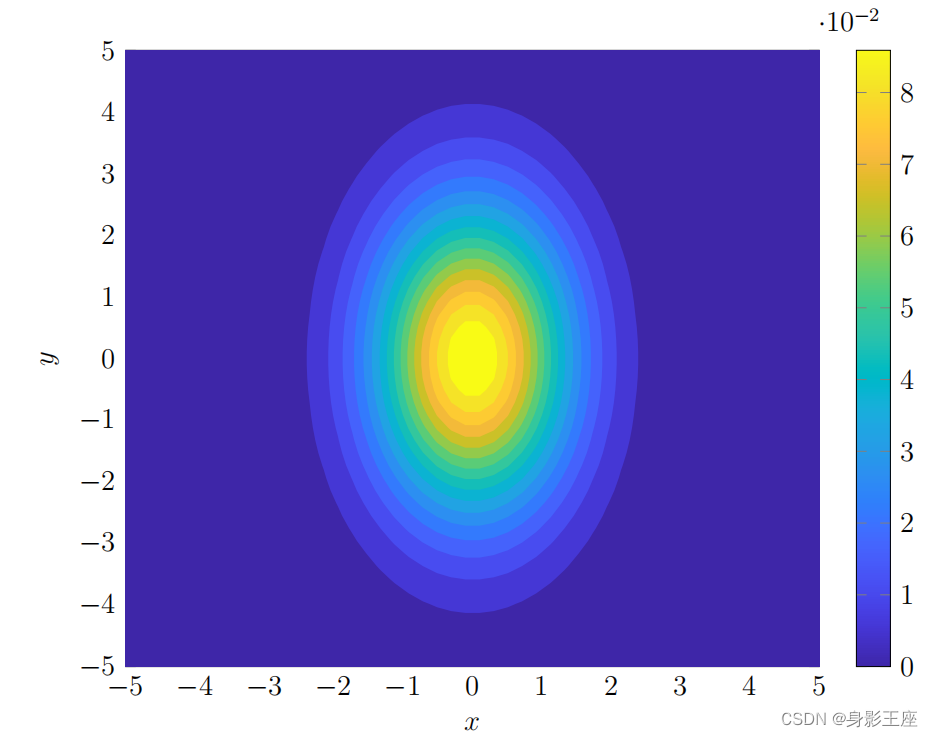
在情况下,见二维高斯分布图,在XY坐标轴上形成的投影(等高图)见下图:
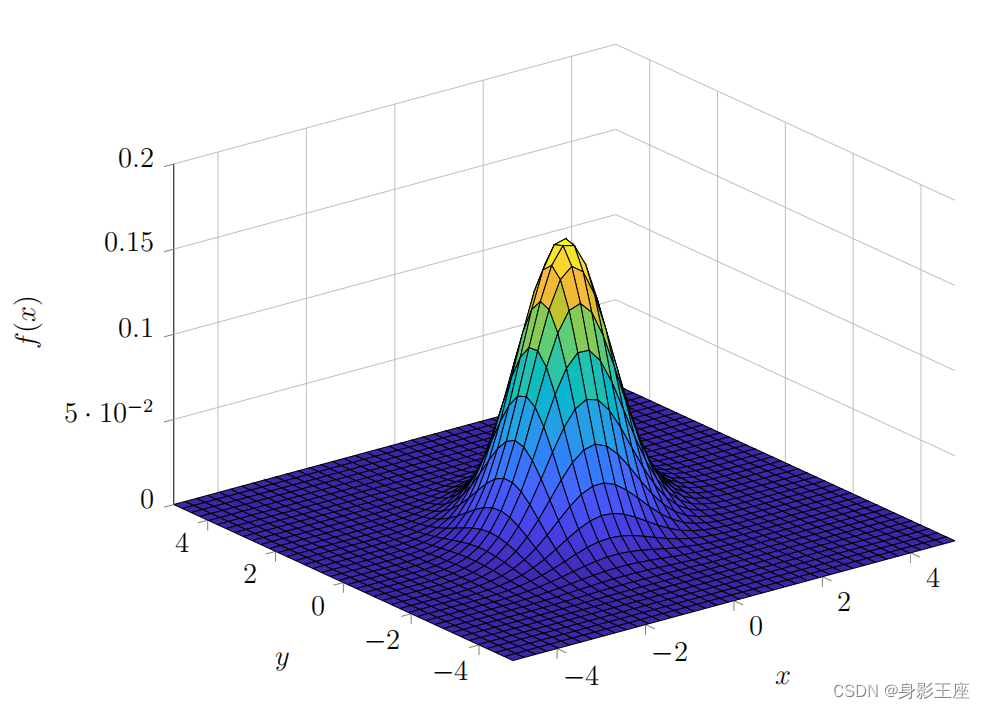

在情况下,见二维高斯分布图,在XY坐标轴上形成的投影(等高图)见下图:
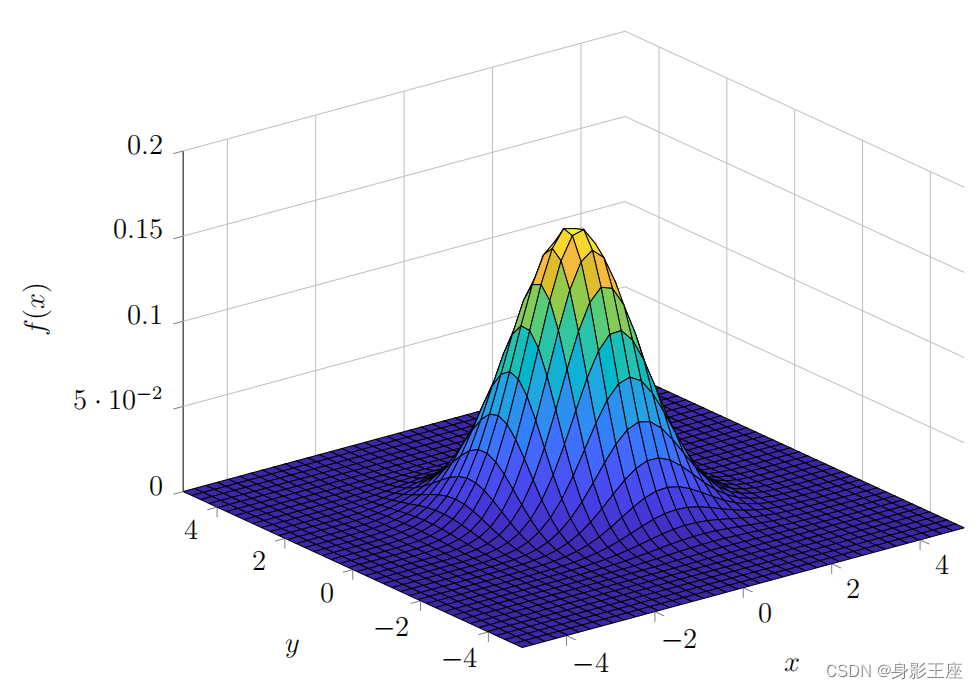
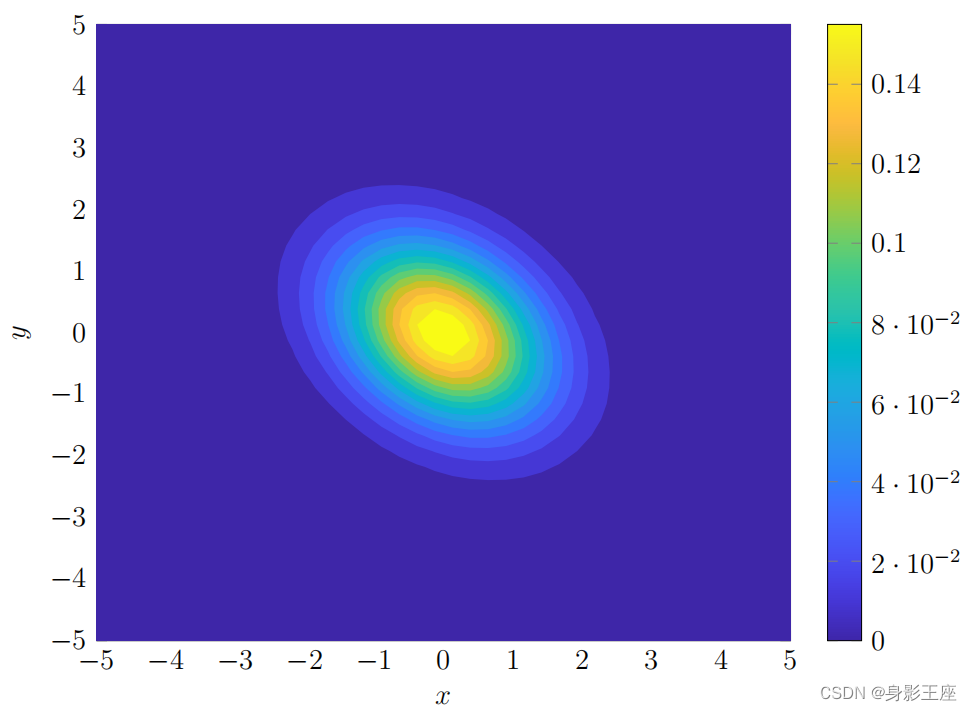
总结:
- 均值表征的是各维变量的中心,其对二维高斯曲面的影响较好理解,它使得整个二维高斯曲面在xoy平面上移动。
- 对于协方差矩阵,对角线上的两个元素,即
和
表征的是x维和y维变量的方差,决定了整个高斯曲面在某一维度上的“跨度”,方差越大,“跨度”越大。
- 协方差矩阵的斜对角线上面的两个元素,即
和
(
)表征的是各维变量之间的相关性:
说明x与y呈正相关(x越大,y越大),其值越大,正相关程度越大;
呈负相关;否则不相关。
版权声明:本文为qq_42148307原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。