AtCoder Beginner Contest 291（Sponsored by TOYOTA SYSTEMS）讲解

蒟蒻来讲题，还望大家喜。若哪有问题，大家尽可提！

Hello, 大家好哇！本初中生蒟蒻讲解一下AtCoder Beginner Contest 291（Sponsored by TOYOTA SYSTEMS）这场比赛的A-F题！

===========================================================================================

A题

原题

Problem Statement

You are given a string $S$ consisting of uppercase and lowercase English letters.

Here, exactly one character of $S$ is uppercase, and the others are all lowercase.

Find the integer $x$ such that the $x$ -th character of $S$ is uppercase.

Here, the initial character of $S$ is considered the $1$ -st one.

Constraints

$S$ is a string of length between $2$ and $100$ , inclusive, consisting of uppercase and lowercase English letters.
$S$ has exactly one uppercase letter.

Input

The input is given from Standard Input in the following format:
$S$

Output

Print the integer $x$ such that the $x$ -th character of $S$ is uppercase.

Sample Input 1

aBc

Sample Output 1

2
The $1$ -st character of aBc is a, the $2$ -nd is B, and the $3$ -rd is c;
the $2$ -nd character is uppercase.

Thus, $2$ should be printed.

Sample Input 2

xxxxxxXxxx

Sample Output 2

7
An uppercase letter X occurs as the $7$ -th character of $S =$ xxxxxxXxxx, so $7$ should be printed.

Sample Input 3

Sample Output 3

思路

这道题仅需循环找到大写字母输出位置即可

代码

/*
------------------Welcome to Your Code--------------
Name:
Contest:AtCoder Beginner Contest 291
Wishes:AK!
------------------Start Writing!!!------------------
*/
#include <iostream>
#define endl '\n'
#define pb(i) push_back(i)

using namespace std;

inline int read()
{
    int w = 1, s = 0;
    char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-') w = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();
    
    return w * s;
}

int main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);
    
    string s;
    
    cin >> s;
    
    s = ' ' + s;
    
    for (int i = 1; i <= s.size(); i ++)
    	if (s[i] >= 'A' && s[i] <= 'Z')
    	{
    		cout << i << endl;
    		return 0;
    	}
    
    return 0;
}

B题

原题

Problem Statement

Takahashi is participating in a gymnastic competition.

In the competition, each of $5 N$ judges grades Takahashi’s performance, and his score is determined as follows:
Invalidate the grades given by the $N$ judges who gave the highest grades.
Invalidate the grades given by the $N$ judges who gave the lowest grades.
Takahashi’s score is defined as the average of the remaining $3 N$ judges’ grades.
More formally, Takahashi’s score is obtained by performing the following procedure on the multiset of the judges’ grades $S$ ( $∣ S ∣ = 5 N$ ):
Repeat the following operation $N$ times: choose the maximum element (if there are multiple such elements, choose one of them) and remove it from $S$ .
Repeat the following operation $N$ times: choose the minimum element (if there are multiple such elements, choose one of them) and remove it from $S$ .
Takahashi’s score is defined as the average of the $3 N$ elements remaining in $S$ .
The $i$ -th $(1\leq i\leq 5N)$ judge’s grade for Takahashi’s performance was $X_i$ points.
Find Takahashi’s score.

Constraints

$1\leq N\leq 100$
$0\leq X_i\leq 100$
All values in the input are integers.

Input

The input is given from Standard Input in the following format:
$N$
$X_1$ $X_2$ $\ldots$ $X_{5N}$

Output

Print Takahashi’s score.

Your answer will be considered correct if the absolute or relative error from the true value is at most $10^{-5}$ .

Sample Input 1

1
10 100 20 50 30

Sample Output 1

33.333333333333336
Since $N = 1$ , the grade given by one judge who gave the highest grade, and one with the lowest, are invalidated.

The $2$ -nd judge gave the highest grade ( $100$ points), which is invalidated.

Additionally, the $1$ -st judge gave the lowest grade ( $10$ points), which is also invalidated.

Thus, the average is $\displaystyle\frac{20+50+30}{3}=33.333\cdots$ .
Note that the output will be considered correct if the absolute or relative error from the true value is at most $10^{-5}$ .

Sample Input 2

2
3 3 3 4 5 6 7 8 99 100

Sample Output 2

5.500000000000000
Since $N = 2$ , the grades given by the two judges who gave the highest grades, and two with the lowest, are invalidated.

The $10$ -th and $9$ -th judges gave the highest grades ( $100$ and $99$ points, respectively), which are invalidated.

Three judges, the $1$ -st, $2$ -nd, and $3$ -rd, gave the lowest grade ( $3$ points), so two of them are invalidated.

Thus, the average is $\displaystyle\frac{3+4+5+6+7+8}{6}=5.5$ .
Note that the choice of the two invalidated judges from the three with the lowest grades does not affect the answer.

思路

这道题读入之后，排序一下，取出从 $[N - 4 N]$ 的和，除以 $3 N$ 即可。

代码

/*
------------------Welcome to Your Code--------------
Name:
Contest:AtCoder Beginner Contest 291
Wishes:AK!
------------------Start Writing!!!------------------
*/
#include <iostream>
#include <algorithm>
#define endl '\n'
#define pb(i) push_back(i)

using namespace std;

const int N = 5e2 + 10;

int sc[N];

inline int read()
{
    int w = 1, s = 0;
    char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-') w = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();
    
    return w * s;
}

int main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);
    
    int n;
    
    cin >> n;
    
    for (int i = 1; i <= n * 5; i ++)
    	cin >> sc[i];
    	
    sort(sc + 1, sc + 1 + n * 5);
    
    int sum = 0;
	for (int i = n + 1; i <= 4 * n; i ++)
		sum += sc[i];
		
	printf("%.7f", sum * 1.0 / (3 * n));
    
    return 0;
}

C题

原题

Problem Statement

Takahashi is on a two-dimensional plane. Starting from the origin, he made $N$ moves.
The $N$ moves are represented by a string of length $N$ as described below:
Takahashi’s coordinates after the $i$ -th move are:
$(x + 1, y)$ if the $i$ -th character of $S$ is R;
$(x - 1, y)$ if the $i$ -th character of $S$ is L;
$(x, y + 1)$ if the $i$ -th character of $S$ is U; and
$(x, y - 1)$ if the $i$ -th character of $S$ is D,
where $(x, y)$ is his coordinates before the move.
Determine if Takahashi visited the same coordinates multiple times in the course of the $N$ moves (including the starting and ending points).

Constraints

$\leq N \leq 2\times 10^5$
$N$ is an integer.
$S$ is a string of length $N$ consisting of R, L, U, and D.

Input

The input is given from Standard Input in the following format:
$N$
$S$

Output

Print Yes if Takahashi visited the same coordinates multiple times in the course of the $N$ moves; print No otherwise.

Sample Input 1

5
RLURU

Sample Output 1

Yes
Takahashi’s coordinates change as follows: $(0,0)\to (1,0)\to (0,0)\to (0,1)\to (1,1)\to (1,2)$ .

Sample Input 2

20
URDDLLUUURRRDDDDLLLL

Sample Output 2

思路

这道题直接暴力一遍即可，看看有没有重复的点，由于简单不再多说~~~

代码

/*
------------------Welcome to Your Code--------------
Name:
Contest:AtCoder Beginner Contest 291
Wishes:AK!
------------------Start Writing!!!------------------
*/
#include <iostream>
#include <set>
#define endl '\n'
#define pb(i) push_back(i)

using namespace std;

typedef pair<int, int> PII;

set<PII> pos; 

inline int read()
{
    int w = 1, s = 0;
    char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-') w = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();
    
    return w * s;
}

int main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);
    
    int n;
    string s;
    
    cin >> n >> s;
    
    s = ' ' + s;
    int x = 0, y = 0;
    pos.insert({x, y});
    for (int i = 1; i <= n; i ++)
    {
    	if (s[i] == 'R') y ++;
    	else if (s[i] == 'L') y --;
    	else if (s[i] == 'U') x --;
    	else x ++;
    	pos.insert({x, y});
    }
    
    if (pos.size() != n + 1) cout << "Yes" << endl;
    else cout << "No" << endl;
    
    return 0;
}

D题

原题

Problem Statement

$N$ cards, numbered $1$ through $N$ , are arranged in a line. For each $KaTeX parse error: Expected 'EOF', got '&' at position 13: i\ (1\leq i &̲lt; N)$ , card $i$ and card $(i + 1)$ are adjacent to each other.
Card $i$ has $A_i$ written on its front, and $B_i$ written on its back. Initially, all cards are face up.
Consider flipping zero or more cards chosen from the $N$ cards.
Among the $2^N$ ways to choose the cards to flip, find the number, modulo $998244353$ , of such ways that:
when the chosen cards are flipped, for every pair of adjacent cards, the integers written on their face-up sides are different.

Constraints

$1\leq N \leq 2\times 10^5$
$1\leq A_i,B_i \leq 10^9$
All values in the input are integers.

Input

The input is given from Standard Input in the following format:
$N$
$A_1$ $B_1$
$A_2$ $B_2$
$\vdots$
$A_N$ $B_N$

Output

Print the answer as an integer.

Sample Input 1

3
1 2
4 2
3 4

Sample Output 1

4
Let $S$ be the set of card numbers to flip.
For example, when $S=\{2,3\}$ is chosen, the integers written on their visible sides are $1, 2$ , and $4$ , from card $1$ to card $3$ , so it satisfies the condition.
On the other hand, when $S=\{3\}$ is chosen, the integers written on their visible sides are $1, 4$ , and $4$ , from card $1$ to card $3$ , where the integers on card $2$ and card $3$ are the same, violating the condition.
Four $S$ satisfy the conditions: ${\},\{1\},\{2\}$ , and ${2,3\}$ .

Sample Input 2

4
1 5
2 6
3 7
4 8

Sample Output 2

Sample Input 3

8
877914575 602436426
861648772 623690081
476190629 262703497
971407775 628894325
822804784 450968417
161735902 822804784
161735902 822804784
822804784 161735902

Sample Output 3

思路

我们这道题可以用 DP（动态规划） 来做，故我们可以继续用我们的闫氏DP分析法！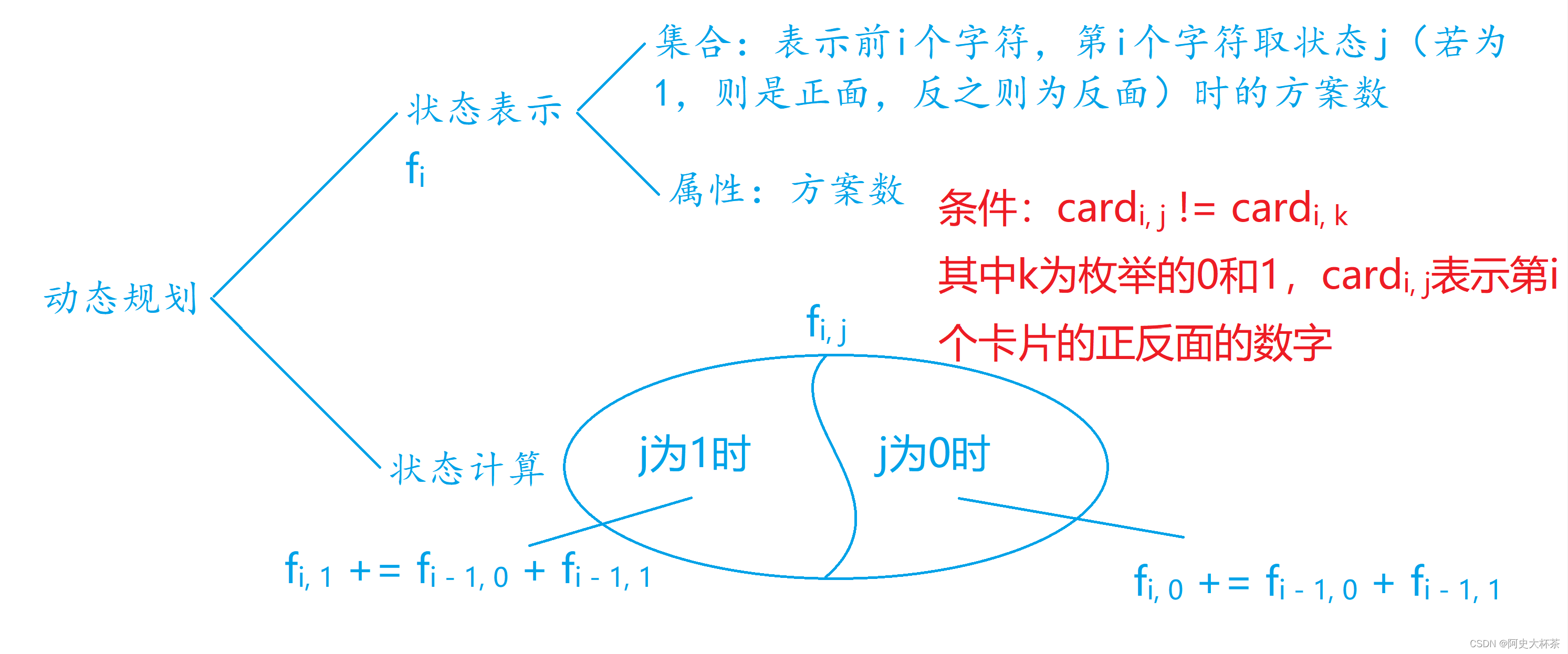
在这里插入图片描述
不过，不要忘了模余数！

代码

/*
------------------Welcome to Your Code--------------
Name:
Contest:
Wishes:AK!
------------------Start Writing!!!------------------
*/
#include <iostream>
#define int long long
#define endl '\n'
#define pb(i) push_back(i)

using namespace std;

const int N = 2e5 + 10, MOD = 998244353;

int n;
int card[N][2];
int f[N][2];

inline int read()
{
    int w = 1, s = 0;
    char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-') w = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();
    
    return w * s;
}

signed main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);
    
	n = read();
    
    for (int i = 1; i <= n; i ++)
    	card[i][0] = read(), card[i][1] = read();
    	
    f[1][0] = f[1][1] = 1;
    for (int i = 2; i <= n; i ++)
    	for (int t = 0; t < 2; t ++)
    		for (int k = 0; k < 2; k ++)
    			if (card[i - 1][t] != card[i][k])
    				f[i][k] = (f[i][k] + f[i - 1][t]) % MOD;
    				
    cout << (f[n][0] + f[n][1]) % MOD << endl;
    
    return 0;
}

E题

原题

Problem Statement

There is a length- $N$ sequence $A=(A_1,\ldots,A_N)$ that is a permutation of $1,\ldots,N$ .
While you do not know $A$ , you know that $KaTeX parse error: Expected 'EOF', got '&' at position 8: A_{X_i}&̲lt;A_{Y_i}$ for $M$ pairs of integers $X_i,Y_i)$ .
Can $A$ be uniquely determined? If it is possible, find $A$ .

Constraints

$\leq N \leq 2\times 10^5$
$\leq M \leq 2\times 10^5$
$1\leq X_i,Y_i \leq N$
All values in the input are integers.
There is an $A$ consistent with the input.

Input

The input is given from Standard Input in the following format:
$N$ $M$
$X_1$ $Y_1$
$\vdots$
$X_M$ $Y_M$

Output

If $A$ can be uniquely determined, print Yes in the first line. Then, print $A_1,\ldots,A_N$ in the second line, separated by spaces.
If $A$ cannot be uniquely determined, just print No.

Sample Input 1

3 2
3 1
2 3

Sample Output 1

Yes
3 1 2
We can uniquely determine that $A = (3, 1, 2)$ .

Sample Input 2

3 2
3 1
3 2

Sample Output 2

No
Two sequences $(2, 3, 1)$ and $(3, 2, 1)$ can be $A$ .

Sample Input 3

4 6
1 2
1 2
2 3
2 3
3 4
3 4

Sample Output 3

Yes
1 2 3 4

思路

这道题我们可以想成一个图， $A_{x_{i}}<A_{y_{i}}$ ，我们可以将 $A_{x_{i}}$ 向 $A_{y_{i}}$ 建一条边，之后其实就是看看能否成为唯一的拓扑序列，所以就是一个BFS宽搜的过程，在过程中用拓扑排序的方法，同时记录每个点的数值，可能说起来有点抽象，那么看看代码吧~~~

代码

/*
------------------Welcome to Your Code--------------
Name:
Contest:
Wishes:AK!
------------------Start Writing!!!------------------
*/
#include <iostream>
#include <vector>
#include <queue>
#define endl '\n'
#define pb(i) push_back(i)

using namespace std;

const int N = 2e5 + 10;

int n, m;
int x, y;
vector<int> g[N];
queue<int> q;
int ru[N], res[N];

inline int read()
{
    int w = 1, s = 0;
    char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-') w = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();
    
    return w * s;
}

void topsort()
{
	for (int i = 1; i <= n; i ++)
		if (!ru[i])
			q.push(i);
			
	int cnt = 0;
	while (q.size())
	{
		if (q.size() != 1) //说明有多种可能
		{
			cout << "No" << endl;
			return;
		}
		
		auto t = q.front();
		q.pop();
		
		res[t] = ++ cnt; //记录
		
		for (auto c : g[t])
			if (!(-- ru[c]))
				q.push(c);
	}
	
	cout << "Yes" << endl;
	for (int i = 1; i <= n; i ++)
		cout << res[i] << " \n"[i == n];
	
}

int main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);
    
    n = read(), m = read();
    
    for (int i = 1; i <= m; i ++)
    	x = read(), y = read(), g[x].pb(y), ru[y] ++;
    	
    topsort();
    
    return 0;
}

今天就到这里了！

大家有什么问题尽管提，我都会尽力回答的！

吾欲您伸手，点的小赞赞。吾欲您喜欢，点得小关注！

原文链接：https://blog.csdn.net/weixin_66946161/article/details/129251147