Review of Combinatorics (HITSZ)
- 1. Pigeonhole Principle
- 2. Permutations and combinations
- 3. Generating Permutations and Combinations
- 4. The Inclusion-Exclusion Principle and Applications (容斥原理)
- 5. Recurrence Relations and Generating Functions
- 6. Special Counting Sequences
- 7. Matchings in bipartite graphs
- 8. Combinatorial designs
- 9. Ploya Counting
- 22年真题回顾
好久没更新博客了,一方面是有其他工作;一方面是假期空闲时间比较想休息,陪陪家人。本次更新主要是关于HITSZ组合数学方面的比较重要的内容,课程老师授课比较用心,值得学习(不过对博主后续研究工作不太有帮助,OK。进入正题。(注:以下PPT内容均来自HITSZ组合数学黄荷娇教授)
1. Pigeonhole Principle
1.1 Conceptions
- The Pigeonhole Principle: If m + 1 m + 1m+1 pigeons are put into m mm pigeonholes, then at least one hole contains two or more pigeons.
- Dirichlet Principle: If n > m n > mn>m pigeons are put into m mm pigeonholes, there’s a hole with more than one pigeon.
- Generalized Pigeonhole Principle: If N NN objects are assigned to k kk places, then at least one place must be assigned at least ⌈ N / k ⌉ \lceil N/k \rceil⌈N/k⌉ objects.
- Pigeonhole Principle-Strong Form: Let q 1 q_1q1,q 2 q_2q2, …, q n q_nqn be positive integers. If q 1 + q 2 + … + q n − n + 1 q_1+ q_2+ …+ q_n - n +1q1+q2+…+qn−n+1 objects are put into n nn boxes, then either the first box contains at least q 1 q_1q1 objects, or the second box contains at least q 2 q_2q2 object, ……, or the n nnth box contains at least q n q_nqn objects.
1.2 Examples
There are several people in the room. Some are acquaintances, others are not. (Being acquainted is a symmetric non-reflexive relationship.) Show that some two people have the same number of acquaintances.
Suppose one can know 0 00 person, 1 11 person, … , N − 1 N-1N−1 persons. Note that 0 00 person cannot exist with N − 1 N - 1N−1 persons. Thus, N NN people can have at most N − 1 N-1N−1 cases for acquaintances. According to the pigeonhole principle, there must be some two people have the same number of acquaintances.
Given m mm integers a 1 a_1a1,$ a_2, … , , …,,…,a_m$, there exists integers k kk and l ll with 0 ≤ k < l ≤ m 0 ≤ k < l ≤ m0≤k<l≤m such that a k + 1 a_{k+1}ak+1 + a k + 2 a_{k+2}ak+2 + … + a l a_lal is divisible by m mm.
Consider the m mm sums a 1 a_1a1, a 1 + a 2 a_1+a_2a1+a2, a 1 + a 2 + a 3 a_1+a_2+a_3a1+a2+a3, …, a 1 + a 2 + a 3 + … + a m a_1+a_2+a_3+…+a_ma1+a2+a3+…+am.
① If any of these sums is divisible by m mm, then the conclusion holds.
② Otherwise, the reminder has only m − 1 m-1m−1 cases (i.e., 1, …, m − 1 m-1m−1). Thus, two sums have the same reminder, suppose s k s_ksk and s l s_lsl. Thus, s l − s k = a k + 1 + . . . + a l s_l-s_k=a_{k+1}+...+a_lsl−sk=ak+1+...+al can be divisible by m mm.
From the integers 1, 2, …, 200, we choose 101 integers. Show that among the integers chosen there are two such that one of them is divisible by the other.
Any integer can be written in the form 2 k × a 2^k × a2k×a, where k ≥ 0 k ≥ 0k≥0 and a aa is odd. Among 1~200, there are only 100 odd numbers. Thus, there must have two numbers have same a aa in the chosen 101 integers. Assume they are 2 k 1 × a 2^{k_1}\times a2k1×a and 2 k 2 × a 2^{k_2}\times a2k2×a. Therefore, they can be divisible by the other.
A bag contains 100 apples, 100 bananas, 100 oranges and 100 pears. How many fruits should be taken out such that we can sure a dozen (12) pieces of them are of the same kind?
According to Pigeonhole Principle-Strong Form, the answer is N = 12 + 12 + 12 + 12 − 4 + 1 = 45 N =12+12+12+12-4+1=45N=12+12+12+12−4+1=45.
A basket of fruit is being arranged out of apples, bananas, and oranges. What is the smallest number of pieces of fruits that should be put in the basket in order to guarantee that either there are at least 8 apples or at least 6 bananas or at least 9 oranges?
According to Pigeonhole Principle-Strong Form, the answer is N = 8 + 6 + 9 − 3 + 1 = 21 N =8+6+9-3+1=21N=8+6+9−3+1=21.
There are 100 people at a party. Each people has an even number of acquaintances. Prove that there are three people at the party with the same number of acquaintances. (it is assumed that no one is acquainted with him or herself.)
Similar to example 1. However, one can only know 2,…, 98 persons (i.e., 49 cases in total). Thus, there are at least ⌈ 100 / 49 ⌉ = 3 \lceil 100/49\rceil =3⌈100/49⌉=3 people at the party with the same number of acquaintances.
1.3 Ramsey
R(m, n): Either there are m mm, each pair of whom are acquainted, or there are n nn, each pair of whom are unacquainted. The Ramsey number is the smallest integer.
Proof of R(3,3) = 6
We argue as follows: Suppose the edges of K6 have been colored red or blue in any way. Consider one of the points p of K6. It meets five edges. Since each of these five edges is colored red or blue, it follows (from the strong form of the pigeonhole principle) that either at least three of them are colored red or at least three of them are colored blue. We suppose that three of the five edges meeting the point p are red. (If three are blue, a similar argument works.) Let the three red edges meeting p join p to points a, b, and c, respectively. Consider the edges which join a, b, c in pairs. If all of these are blue, then a, b, c determine a blue K3. If one of them, say the one joining a and b, is red, then p, a, b determine a red K3. Thus, we are guaranteed either a red K3 or a blue K3.
2. Permutations and combinations
- r-permutation: P ( n , r ) P(n, r)P(n,r)
- r-combinations: C ( n , r ) C(n, r)C(n,r)
- infinite multiset r-combinations (k types): C ( n + k − 1 , k − 1 ) C(n+k-1,k-1)C(n+k−1,k−1)
- infinite multiset r-permutations (k types): k r k^rkr
- finite multiset (repletion) r-combinations: Using IEP.
3. Generating Permutations and Combinations
3.1 Generating Permutations
Mobile Integer
Given 2 → 6 → 3 → 1 → 5 → 4 → \mathop{2}\limits ^{\rightarrow}\mathop{6}\limits ^{\rightarrow}\mathop{3}\limits ^{\rightarrow}\mathop{1}\limits ^{\rightarrow}\mathop{5}\limits ^{\rightarrow}\mathop{4}\limits ^{\rightarrow}2→6→3→1→5→4→. 6, 3, 5 are mobile integers
Algorithm

Example

3.2 Inversion in Permutations
- Inversion Numbers
Given 51234. Pairs (5, 1), (5, 2), (5, 3), (5, 4) are inversions. Thus, 1, 1, 1, 1, 0 is the inversion sequence. - Generating permutations according to inversion sequence.
- Algorithm 1. Write n, n-1, … 1. (Disadvantage: without location information)
- Algorithm 2. Write 1, …, n
3.3 Generating Combinations
Base-2 algorithm, i.e., Binary Addition Method.
3.4 Generating r-combinations
A precedes B: the smallest integer which is in their union A∪B but not in their intersection A ∩ B is in A
Algorithm

- Example

4. The Inclusion-Exclusion Principle and Applications (容斥原理)
4.1 IEP Conceptions
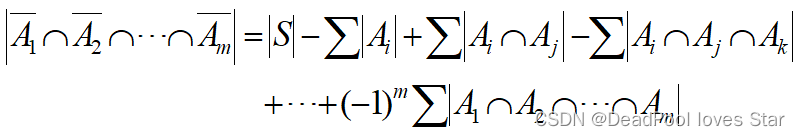
4.2 Derangement
Definition: the numbers are out of its natural position.
Equations:
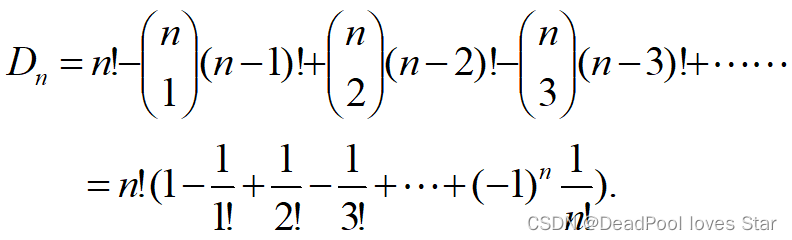
4.3 Chessboard Polynomial (棋盘多项式)
- Basics
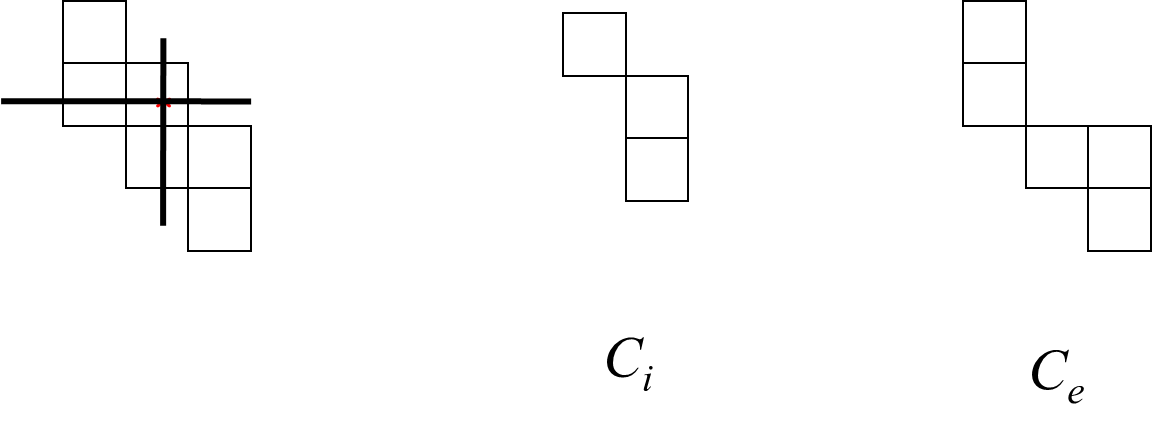
R ( C ) = x R ( C i ) + R ( C e ) R(C)=xR(C_i)+R(C_e)R(C)=xR(Ci)+R(Ce)
- Example
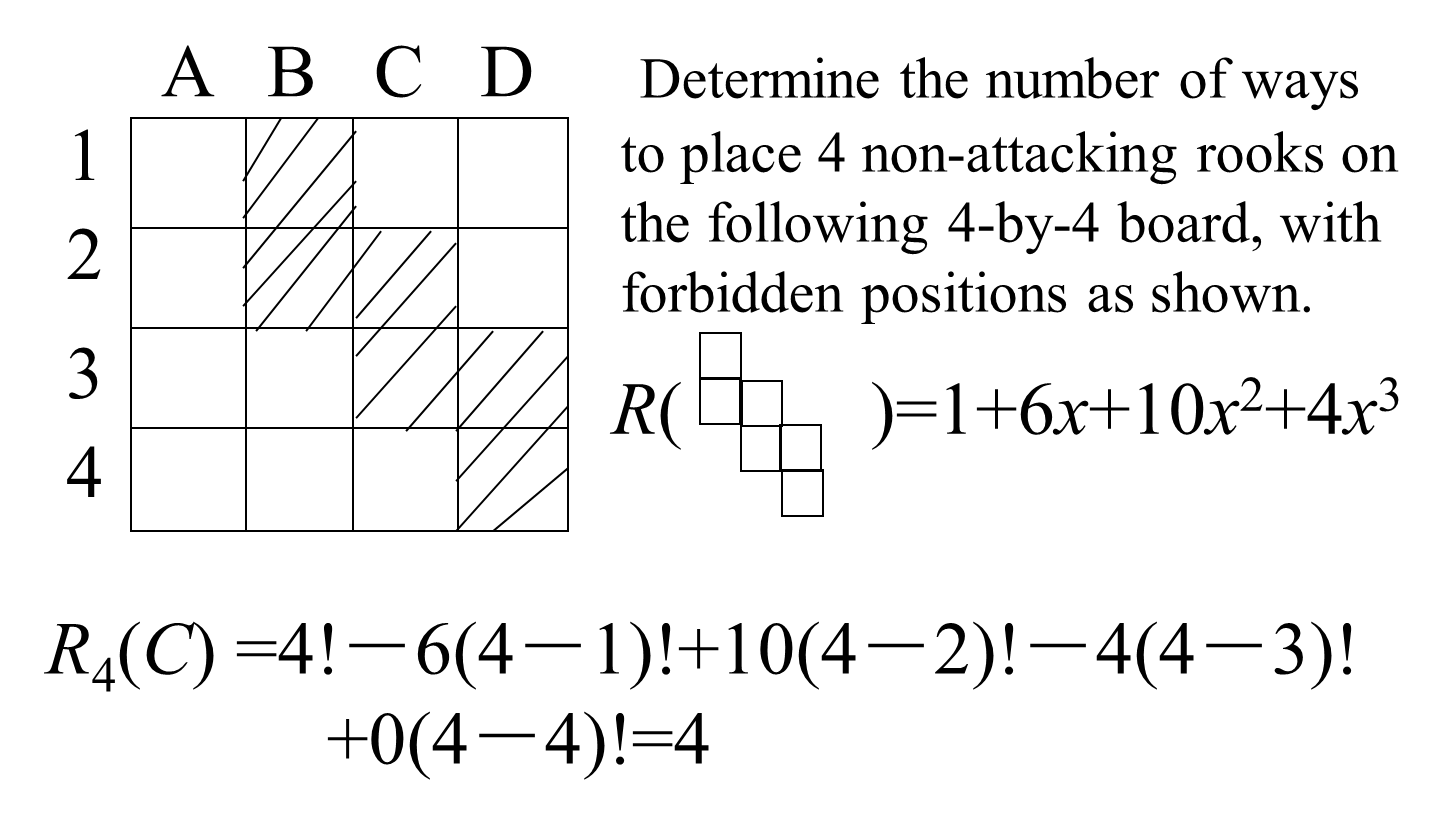
5. Recurrence Relations and Generating Functions
- For Combinations: ( 1 + x + x 2 + . . . ) ( 1 + x + x 2 + . . . ) ( 1 + x + x 2 + . . . ) (1+x+x^2+...)(1+x+x^2+...)(1+x+x^2+...)(1+x+x2+...)(1+x+x2+...)(1+x+x2+...)
- For Permutations: ( 1 + x + x 2 / n 2 + . . . ) ( 1 + x + x 2 / n 2 + . . . ) ( 1 + x + x 2 / n 2 + . . . ) (1+x+x^2/n^2+...)(1+x+x^2/n^2+...)(1+x+x^2/n^2+...)(1+x+x2/n2+...)(1+x+x2/n2+...)(1+x+x2/n2+...)
6. Special Counting Sequences
6.1 Catalan Number
- Catalan Number: C a t n = 1 n + 1 C 2 n n Cat_n=\frac{1}{n+1}C^{n}_{2n}Catn=n+11C2nn
- Meanings: The number of sequences a 1 , a 2 , … , a 2 n a_1, a_2, …, a_{2n}a1,a2,…,a2n of 2 n 2n2n terms that can be formed by using n nn + 1 +1+1’s and n nn − 1 -1−1’s whose partial sums satisfy a 1 + a 2 + … + a k ≥ 0 , ( k = 1 , 2 , … , 2 n ) a_1+ a_2+ …+ a_k ≥ 0 , (k=1,2, …, 2n)a1+a2+…+ak≥0,(k=1,2,…,2n) equals the n nnth Catalan number C a t n Cat_nCatn.
- Recurrence relation: C a t n C a t n − 1 = 4 n − 2 n + 1 \frac{Cat_n}{Cat_{n-1}}=\frac{4n-2}{n+1}Catn−1Catn=n+14n−2
- Pseudo-Catalan Number: C n ∗ = n ! C n − 1 C^*_n=n!C_{n-1}Cn∗=n!Cn−1
6.2 Difference sequences and Stirling numbers
6.2.1 Difference Sequences
- h n = c 0 C ( n , 0 ) + c 1 C ( n , 1 ) + . . . + c p C ( n , p ) h_n=c_0C(n,0)+c_1C(n,1)+...+c_pC(n,p)hn=c0C(n,0)+c1C(n,1)+...+cpC(n,p), where c i c_ici is the 0th diagonal of the difference table.
- ∑ k = 0 n h k = c 0 C ( n + 1 , 1 ) + c 1 C ( n + 1 , 2 ) + . . . + c p C ( n + 1 , p + 1 ) \sum_{k=0}^n h_k=c_0C(n+1,1) + c_1C(n+1,2)+...+ c_pC(n+1,p+1)∑k=0nhk=c0C(n+1,1)+c1C(n+1,2)+...+cpC(n+1,p+1)
6.2.2 Stirling number of the second kind
- Definition: Let h n = n p h_n= n^phn=np, the 0th diagonal of its difference table is c ( p , 0 ) c(p,0)c(p,0),c ( p , 1 ) c(p,1)c(p,1)…c ( p , p ) c(p,p)c(p,p). Then, S ( p , k ) = c ( p , k ) k ! S(p,k)=\frac{c(p,k)}{k!}S(p,k)=k!c(p,k)
- Recurrence: S ( p , k ) = k S ( p − 1 , k ) + S ( p − 1 , k − 1 ) S(p,k)=kS(p-1,k)+S(p-1,k-1)S(p,k)=kS(p−1,k)+S(p−1,k−1)
- The Stirling number of the second kind S ( p , k ) S(p,k)S(p,k) counts the number of partitions of a set of p elements into k indistinguishable boxes in which no box is empty
6.2.3 Partition Number S s h a r p ( p , k ) S^{sharp}(p,k)Ssharp(p,k)
- S s h a r p ( s , p ) = k ! S ( p , k ) S^{sharp}(s,p)=k!S(p,k)Ssharp(s,p)=k!S(p,k).
- Similar to 2th Stirling Number but with distinguishable boxes.
6.2.4 Bell Number
- B p = S ( p , 0 ) + S ( p , 1 ) + . . . + S ( p , p ) B_p=S(p,0)+S(p,1)+...+S(p,p)Bp=S(p,0)+S(p,1)+...+S(p,p)
- The Bell number B p B_pBp is the number of partitions of a set of p elements into non-empty, indistinguishable boxes. (The number of the box is not clarified).
6.2.5 Stirling Number of the first kind
- The Stirling number s ( p , k ) s(p, k)s(p,k) of the first kind counts the number of arrangements of p objects into k non-empty circular permutations.
- Recurrence: s ( p , k ) = ( p − 1 ) s ( p − 1 , k ) + s ( p − 1 , k − 1 ) s(p,k)=(p-1)s(p-1,k)+s(p-1,k-1)s(p,k)=(p−1)s(p−1,k)+s(p−1,k−1)
6.3 Partition Number
- Definition

- Calculation: using generating functions to calculate. Since λ = a n ∗ n + . . . + a 1 ∗ 1 \lambda=a_n*n+...+a_1*1λ=an∗n+...+a1∗1. Let f 1 = a 1 ∗ 1 f_1=a_1*1f1=a1∗1, … f n = a n ∗ n f_n=a_n*nfn=an∗n. Thus, f n f_nfn is multiply of n nn. That is to say:
g ( x ) = ( 1 + x + x 2 + . . . ) ( 1 + x 2 + x 4 + . . . ) . . . ( 1 + x n + x 2 n + . . . ) = Π k = 1 n 1 1 − x k g(x)=(1+x+x^2+...)(1+x^2+x^4+...)...(1+x^n+x^{2n}+...)=\Pi_{k=1}^n\frac{1}{1-x^k}g(x)=(1+x+x2+...)(1+x2+x4+...)...(1+xn+x2n+...)=Πk=1n1−xk1
7. Matchings in bipartite graphs
7.1 Bipartite Graph
- Matching: A matching in a graph G is a set of non-loop edges with no shared endpoints
- Maximal Matching: A maximal matching in a graph is a matching that cannot enlarged by adding an edge.
- Maximum Matching: A maximum-matching is a matching of maximum size among all matchings in the graph.
- M-Saturated Vertices: The vertices incident to the edges of a matching M (匹配M中的点).
- M-Unsaturated Vertices: The vertices which are not saturated by M (匹配M外的点).
- M-Alternating Path: Given a matching M, and an M-Alternating path is a path that alternates between edges in M and edges not in M (M中的边和非M中的边交错).
- M-Augmenting Path: An M-Alternating path whose endpoints are unsaturated by M (交织路径但端点是非饱和点).
- A Matching M is a Max-Matching in G iff G has no M-Augmenting path (最大匹配当且仅当图G中没有增广路径).
- Vertex Cover: A vertex cover of a graph G is a set S ⊆ V ( G ) S\subseteq V(G)S⊆V(G) that contains at least one endpoint of every edge (点覆盖了所有边).
- Min-Cover: A cover with the smallest number of vertices.
- The number of edges in Max-Matching ≤ \le≤ The number of vertices in Min-Cover.
- Max-Matching Algorithm: Scan and Label.
Theorems
Hall’s Theorem: An X , Y X,YX,Y-bigraph G has a matching that saturates X iff ∣ N ( S ) ∣ > = ∣ S ∣ |N(S)|>=|S|∣N(S)∣>=∣S∣ for all S ⊆ X S\subseteq XS⊆X
The Marriage Theorem: An X , Y X,YX,Y-bigraph G with ∣ X ∣ = ∣ Y ∣ |X|=|Y|∣X∣=∣Y∣ has a perfect matching iff ∣ N ( S ) ∣ > = ∣ S ∣ |N(S)|>=|S|∣N(S)∣>=∣S∣ for all S ⊆ X S\subseteq XS⊆X.
Perfect matching is a matching M such that all the vertices in G are saturated.
Konig Theorem: If G is a bipartiite graph, then the maximum size of a matching in G equals to the minimum size of a vertex cover in G (二部图最大匹配与最小顶点覆盖数相同).
7.2 Systems of Distinct Representatives (SDR)
Definitions
Choose distinct representatives from given groups.
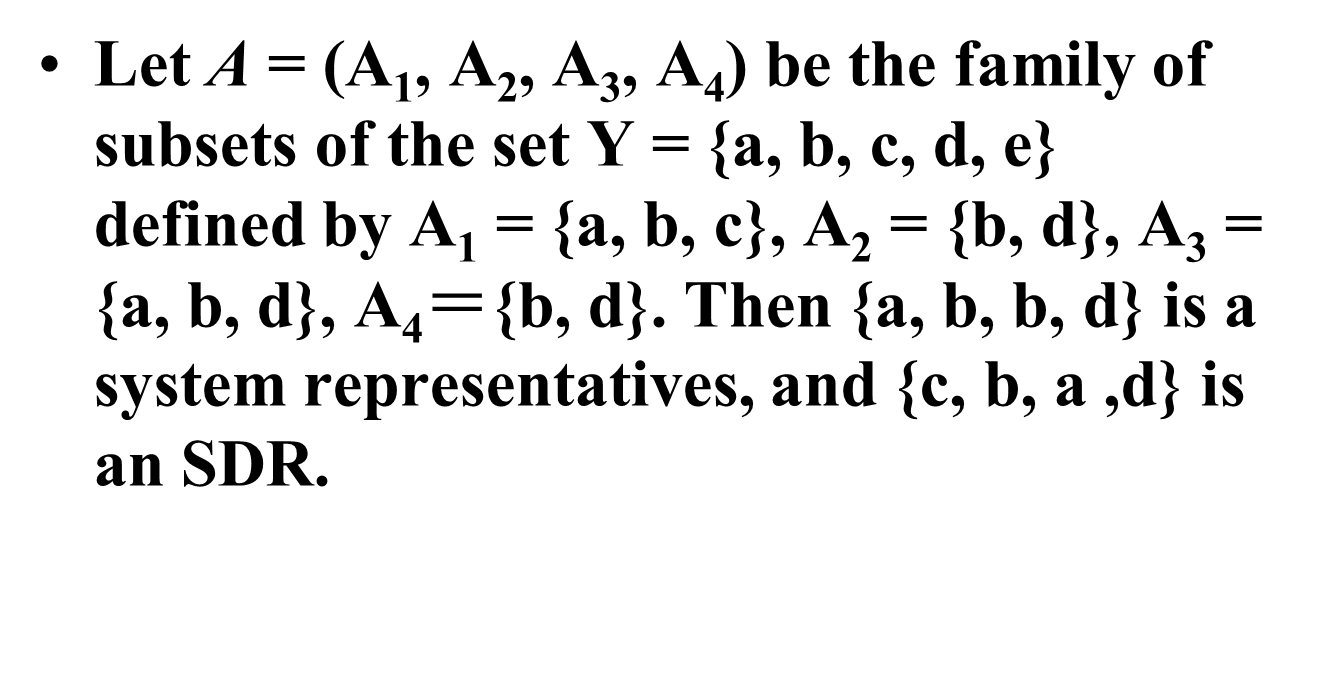
- How to calculate the largest number of sets of A which can be chosen such that they have an SDR

7.3 Stable Marriages (Deferred acceptance algorithm)
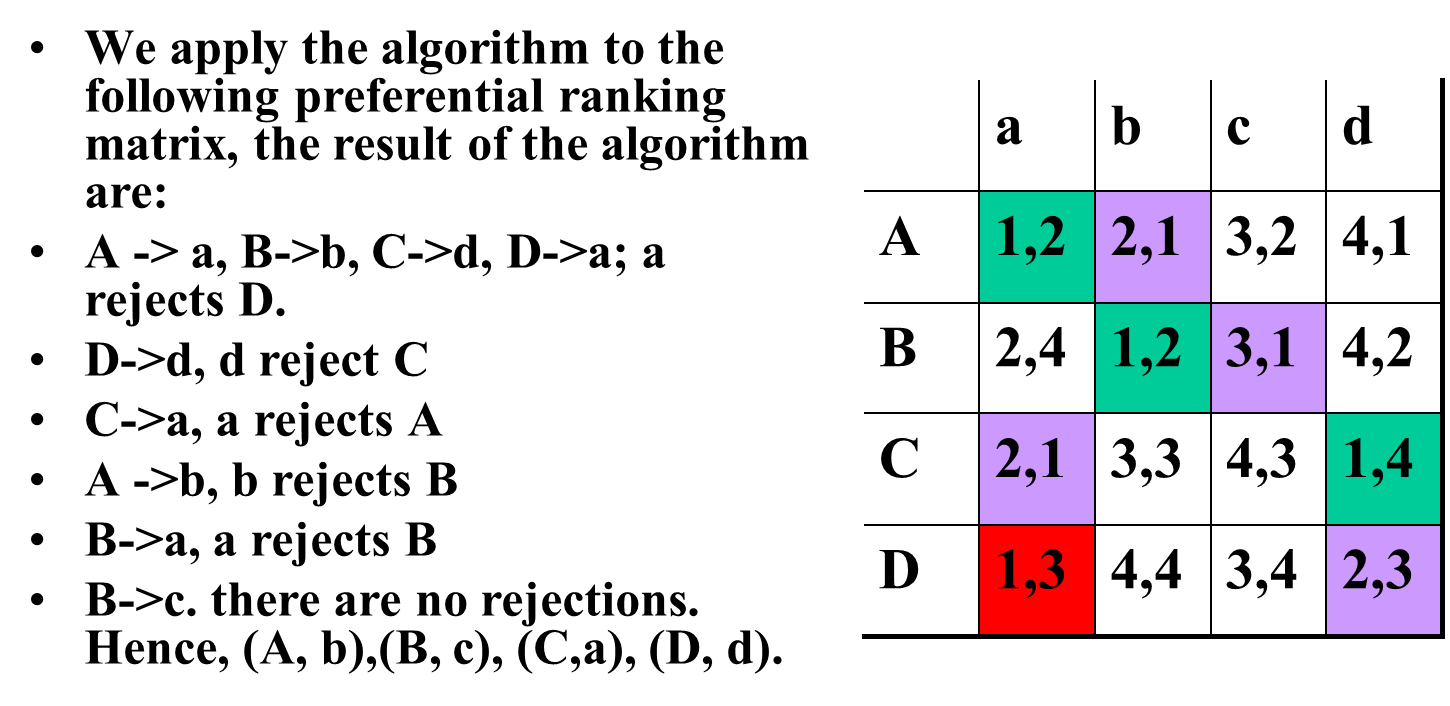
Women-Optimal Stable Marriages is equivalent to Men-Optimal Stable Marriages.
8. Combinatorial designs
8.1 Basics
Parameters
b bb 分组块数 v vv 属性数 k kk 每个分组中的属性数 r rr 每个属性存在r rr个分组中 λ \lambdaλ 每对属性存在λ \lambdaλ个分组中 BIBD (Balanced Incomplete Block Design)
- b ≥ v b\ge vb≥v
- r = λ ( v − 1 ) / ( k − 1 ) r=\lambda(v-1)/(k-1)r=λ(v−1)/(k−1)
- λ < r \lambda<rλ<r
- b k = v r bk=vrbk=vr
SBIBD (Symmetry Balanced Incomplete Block Design): b = v b=vb=v
8.2 Difference set mod v vv and Starter Block

8.3 Steiner Triple Systems
Definition: BIBD with k = 3 k=3k=3.
Important Theorem: If there are Steiner triple systems of index λ = 1 \lambda =1λ=1 with v vv and w ww varieties, respectively, then there is a Steiner triple system of index λ = 1 \lambda =1λ=1 with v w vwvw varieties.
- Row. Row elements are in B 2 B_2B2.
- Column. Column elements are in B 1 B_1B1.
- Cross. Cross elements are in both B 1 B_1B1 and B 2 B_2B2.
Resolvability Class/Resolvable. The Steiner Triple System is Resolvable while each part is called a resolvability class.

8.4 Latin Squares
8.4.1 Basics
Definition: Each of the rows and each of the columns of a Latin square is a permutation of the elements of S.
Partitions

- Properties of Latin Squares (How to judge a Latin Sqaure)

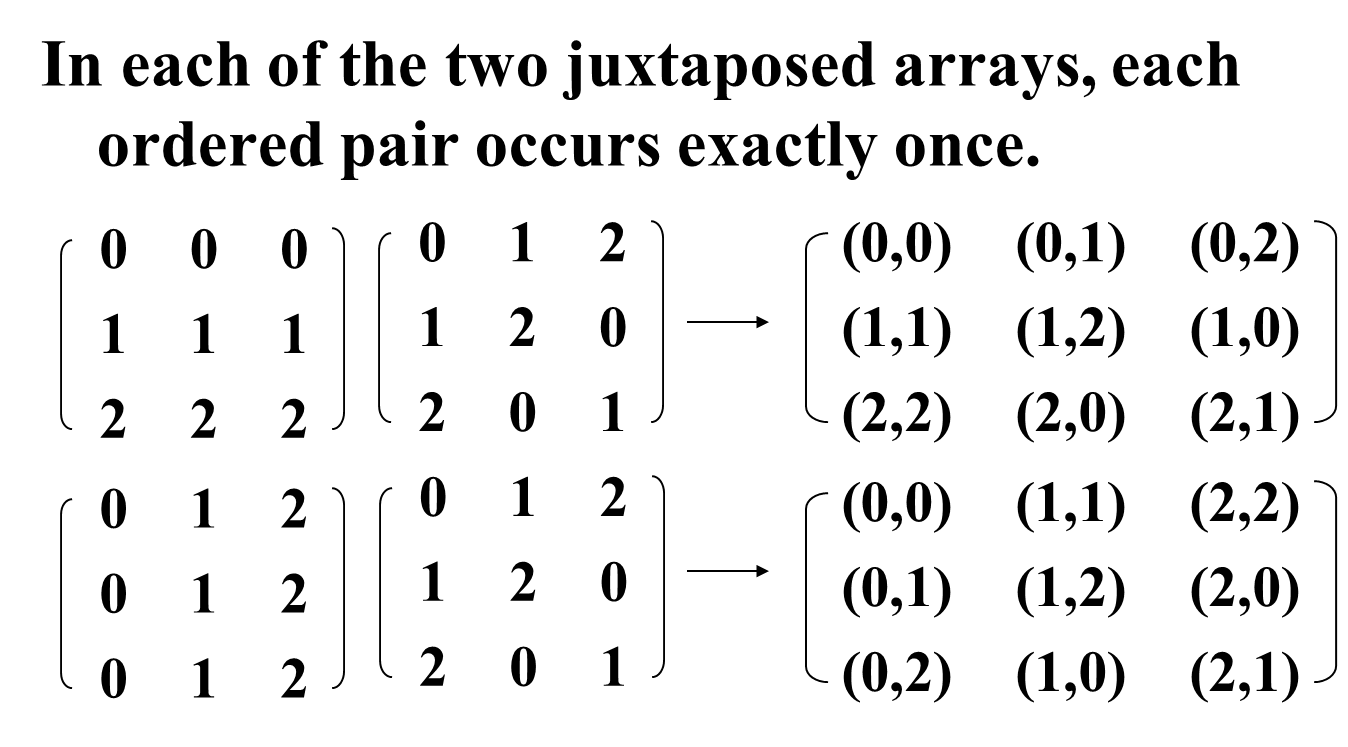
Orthogonal: In the juxtaposed array A × B A × BA×B (see above), each of the ordered pairs ( i , j ) (i, j)(i,j) of integers in Z n Z_nZn occurs exactly once.
MOLS (Mutually Orthogonal Latin Squares): A 1 , A 2 , . . . , A k A_1, A_2,...,A_kA1,A2,...,Ak are Latin squares of order n nn, each pair ( A i , A j ) (A_i,A_j)(Ai,Aj) is orthogonal.
The Largest Number of MOLS is denoted as N ( n ) N(n)N(n) (where the Latin squares all of order n nn).
Latin Rectangle: Let m mm and n nn be integers with m ≤ n m ≤ nm≤n. An m mm-by-n nn Latin rectangle, based on the integers in Z n Z_nZn, is an m mm-by-n nn array such that no integers is repeated in any row or in any column.
Semi-Latin Square: Latin Square with many “holes”.
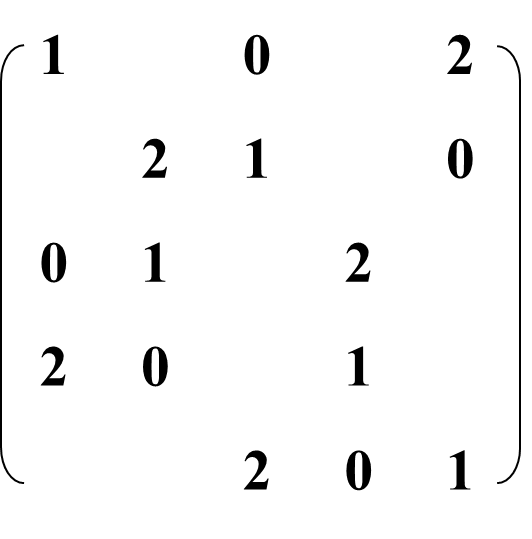
8.4.2 Constructing Latin squares
- Addition mod n

- Multiplicative Inverse

- Field Arithmetic
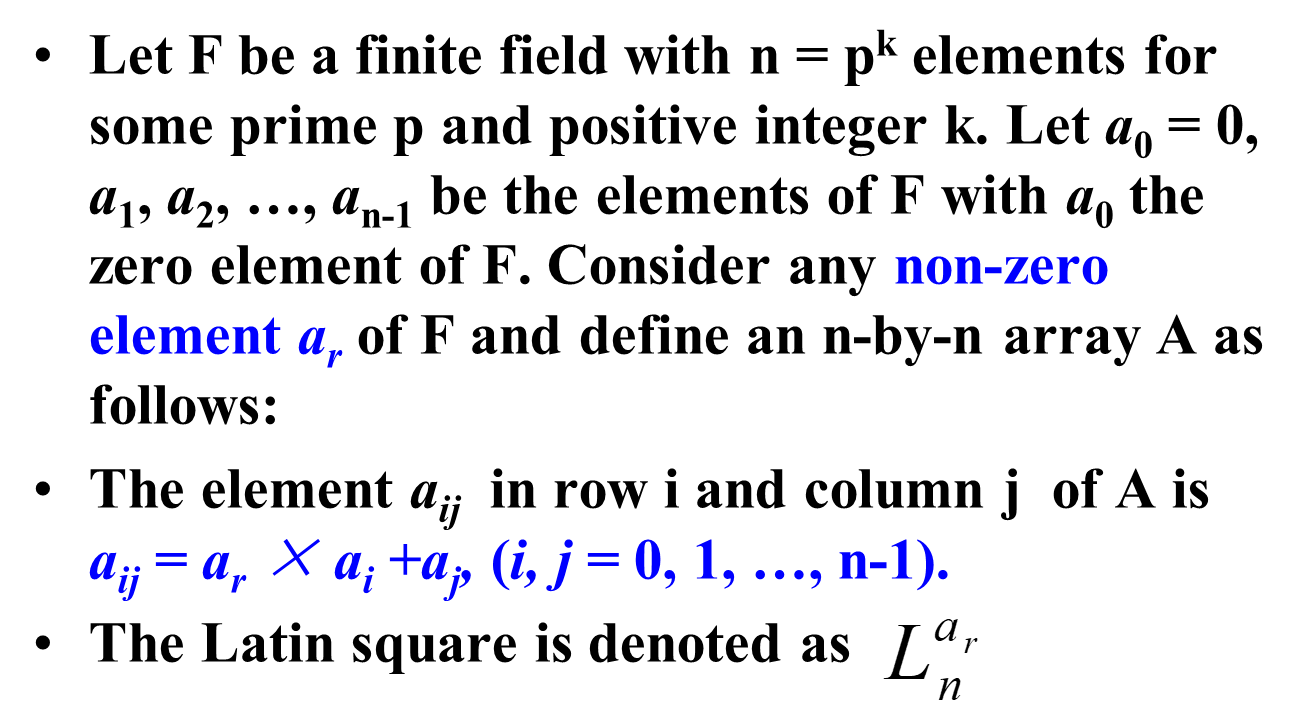
8.4.3 Important Theorems
- Let n nn be a prime number. Then L n 1 , L n 2 , … , L n n − 1 L_n^1, L_n^2, …, L_n^{n-1}Ln1,Ln2,…,Lnn−1 are n − 1 n-1n−1 MOLS of order n nn.
- Let n = p k n=p^kn=pk be an integer and p pp is a prime number. Then L n a 1 , L n a 2 , … , L n a n − 1 L_n^{a_1}, L_n^{a_2}, …, L_n^{a_{n-1}}Lna1,Lna2,…,Lnan−1 are n − 1 n-1n−1 MOLS of order n nn.
8.4.4 Construction of BIBD with MOLS
Key Idea: using n − 1 n-1n−1 MOLS of order n nn with R n R_nRn, S n S_nSn to construct a block design with parameters: ① v = n 2 v=n^2v=n2 ② k = n k=nk=n ③ λ = 1 \lambda=1λ=1 ④ r = n + 1 r=n+1r=n+1 ⑤ b = n 2 + n b=n^2+nb=n2+n
Algorithm (① list the table with v vv items ② find the group by the following array: R n , S n , A i R_n, S_n, A_iRn,Sn,Ai)

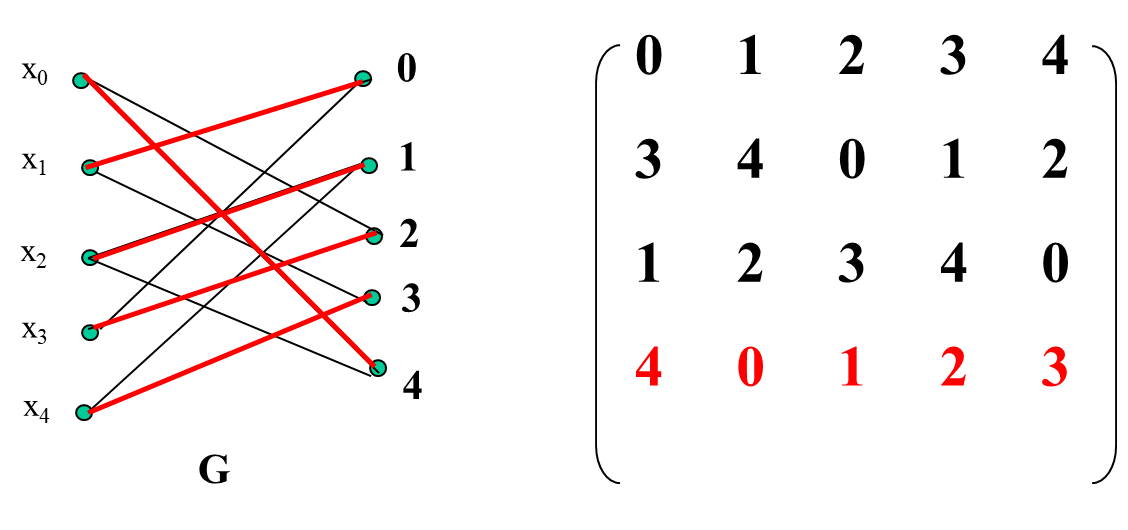
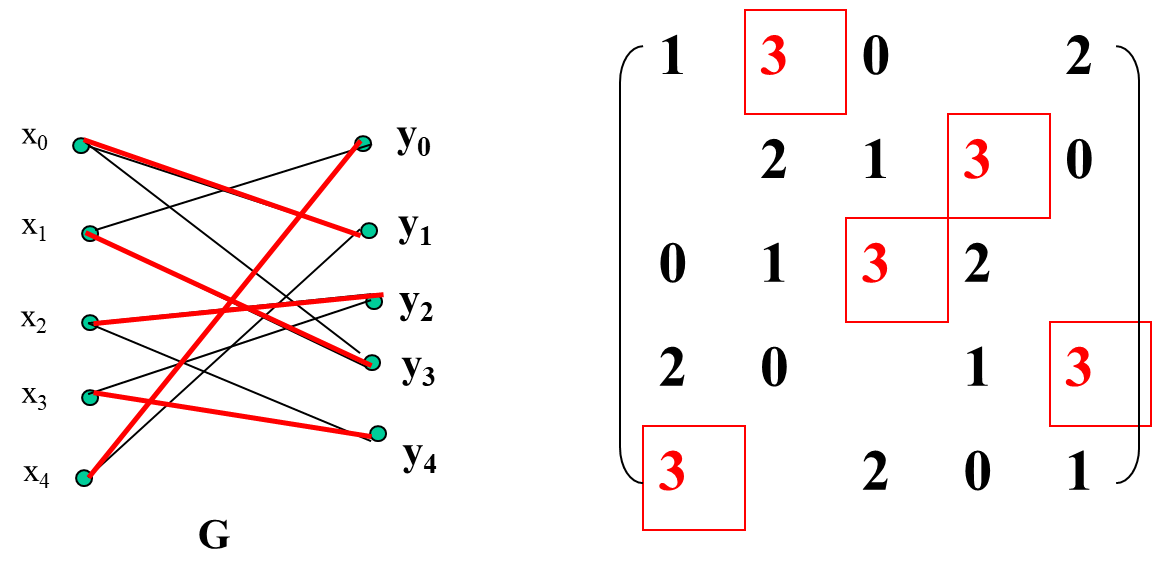
8.4.6 Completion of Latin Squares
Using Bi-graph and perfect matching to complete Latin Rectangle (Since it is a K-regular graph, perfect matching must exist).
Latin Rectangle (X is row, Y is missing number)
Semi-Latin Square (X is row, Y is missing column)
9. Ploya Counting
9.1 Group Basics
Permutation Group
- Closure under composition (置换加法封闭)
- Identity (有恒等置换)
- Closure under inverse (置换都有逆元)
G = { l } G = \{l\}G={l} is a permutation group.
Symmetric Group
- The set S n S_nSn of all permutations of X = { 1 , 2 , … , n } X = \{1, 2, …, n\}X={1,2,…,n} is a permutation group, called the symmetric group of order n nn.
Dihedral Group (二面体群)
A Group with order 2 n 2n2n consisting of n nn Rotations and n nn Reflections.

9.2 Burnside’s Theorem
Stabilizer: G ( c ) = { f : f i n G , f ∗ c = c } G(c)=\{f: f\ in\ G, f*c=c\}G(c)={f:f in G,f∗c=c}, 即所有让染色c cc不变的置换;C ( f ) = { c : c i n G , f ∗ c = c } C(f)=\{c:c\ in\ G, f*c=c\}C(f)={c:c in G,f∗c=c},即所有在置换f ff下保持不变的染色方案
Theorem: For each coloring c cc, the stabilizer G ( c ) G(c)G(c) of c cc is a permutation group. Moreover, for any permutations f ff and g gg in G GG, g ∗ c = f ∗ c g*c = f*cg∗c=f∗c if and only if f − 1 g f^{-1}gf−1g is in G ( c ) G(c)G(c).
Corollary: 所有与c相同的着色方案为∣ G ∣ / ∣ G ( c ) ∣ |G|/|G(c)|∣G∣/∣G(c)∣个
Burnside Theorem
∑ ∣ C ( f ) ∣ = ∑ ∣ G ( c ) ∣ \sum |C(f)|=\sum |G(c)|∑∣C(f)∣=∑∣G(c)∣ and using the Corollary
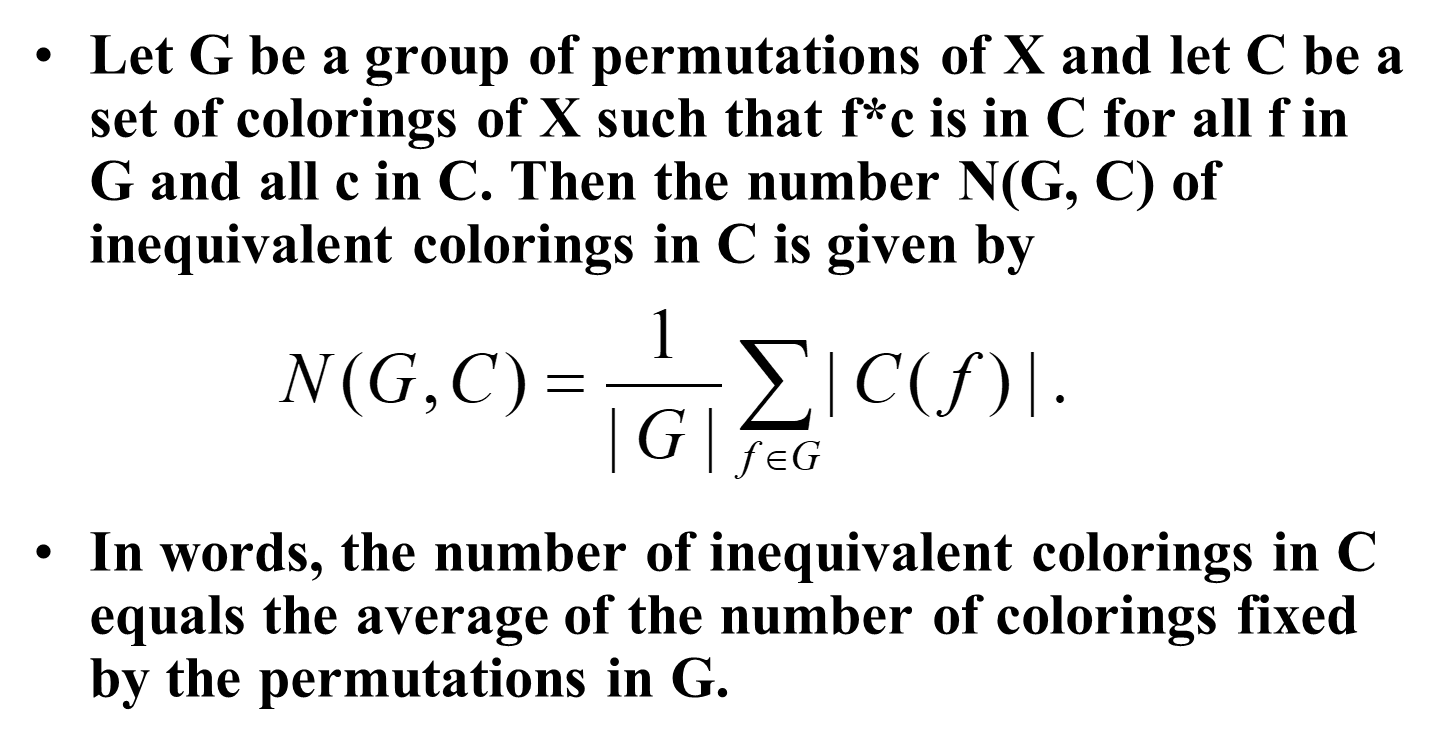
9.3 Polya’s counting formula
Factorization, see below:
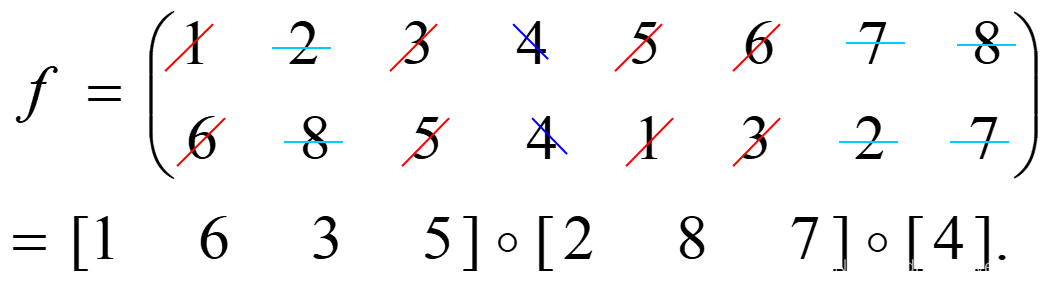
#( f ) (f)(f) is the number of cycles in the cycle factorization of a permutation f. In the above example, #( f ) = 3 (f)=3(f)=3.
Type of a permutation
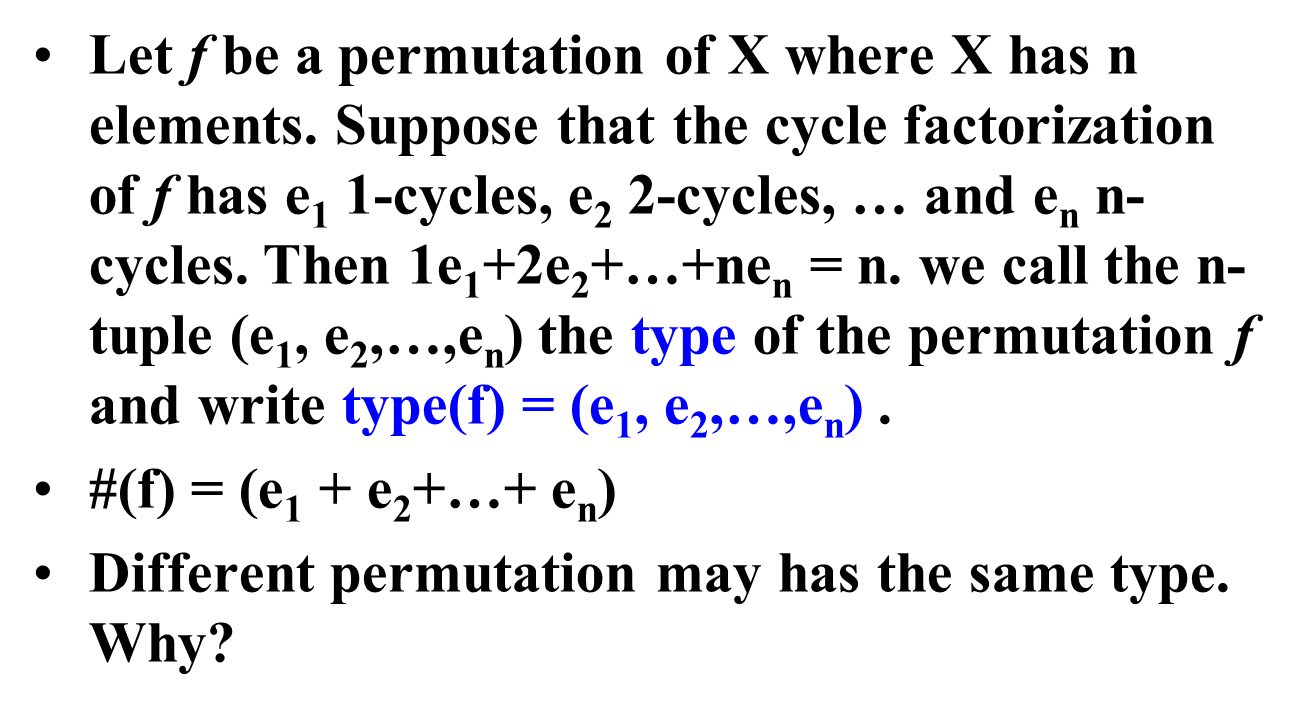
Generating Function: ∑ m o n ( f ) = ∑ z 1 e 1 z 2 e 2 . . . z n e n \sum mon(f)=\sum z_1^{e_1}z_2^{e_2}...z_n^{e_n}∑mon(f)=∑z1e1z2e2...znen
Cycle Index: Generating function divided by ∣ G ∣ |G|∣G∣, i.e.,
P G ( z 1 , z 2 , . . . , z n ) = 1 ∣ G ∣ ∑ z 1 e 1 z 2 e 2 . . . z n e n P_G(z_1,z_2,...,z_n)=\frac{1}{|G|}\sum z_1^{e_1}z_2^{e_2}...z_n^{e_n}PG(z1,z2,...,zn)=∣G∣1∑z1e1z2e2...znen∣ N ( G , C ) ∣ = P G ( k , k , . . . , k ) |N(G,C)|=P_G(k,k,...,k)∣N(G,C)∣=PG(k,k,...,k)
Playa Counting


22年真题回顾
第一部分:填空题(无需写出详细过程,30分)
顺序记不太清了,以下不分先后
- 用1、2、3、4、5组成4个数字的偶数共多少种方法?
- 非负整数解问题,类似e 1 + e 2 + e 3 + e 4 = n e1+e2+e3+e4=ne1+e2+e3+e4=n,对e i eiei有限制
- { 1 , 2 , 3 , 4 , 5 , 6 } \{1, 2, 3, 4, 5, 6\}{1,2,3,4,5,6}排序,逆序数为14的排序数有几个?(最大为15,654321,相邻两两交换即为所求)
- Forbidden Chessboard问题
- ∑ k = 0 n k 4 = ? \sum_{k=0}^n k^4=?∑k=0nk4=?(差分序列部分公式Difference Sequence)
- 填充Latin Rectangle矩阵(二部图匹配)
- { 1 , 2 , 3 , 4 , 5 , 6 } \{1,2,3,4,5,6\}{1,2,3,4,5,6}找4组合中1356的位置
- 递归关系问题:类似用三种颜色图1-n的棋盘,然后两个红色不能连续
- { 1 , 2 , 3 , . . . , 3 n } \{1,2,3,...,3n\}{1,2,3,...,3n}里选多少个数能够保证一定有两个数的差最多为2(鸽巢原理)
- f ∗ c f*cf∗c问题
第二部分:问答题(70分,1、2题5分,剩下各10分)
- 判断数字是否有乘法逆元并求其逆元(GCD(p,n)=1)
- 鸽巢原理:等边三角形,放入m mm个点,问m mm至少为多少时一定有两个点间距最大为1/2(等分成4个部分,m=5)
- 证明:
k n = C ( k , 1 ) ∗ 1 ! ∗ S ( n , 1 ) + C ( k , 2 ) ∗ 2 ! ∗ S ( n , 2 ) + . . . + C ( k , n ) ∗ n ! ∗ S ( n , n ) k^n=C(k, 1)*1!*S(n,1)+C(k, 2)*2!*S(n,2)+...+C(k, n)*n!*S(n,n)kn=C(k,1)∗1!∗S(n,1)+C(k,2)∗2!∗S(n,2)+...+C(k,n)∗n!∗S(n,n)
(思路:左边是把n个元素放到k个可区分盒子中,盒子可空的方法数;右边是1个盒子不空、2个盒子不空……n个盒子不空的方法数之和,显然二者等价) - 根据生成函数求h n h_nhn:
( x + x 2 + . . . + x 5 ) ( 1 + x + x 2 + . . . + x 7 ) ( x 4 + x 5 + . . . + x 8 ) ( x 2 + x 3 + . . . + x 6 ) (x+x^2+...+x^5)(1+x+x^2+...+x^7)(x^4+x^5+...+x^8)(x^2+x^3+...+x^6)(x+x2+...+x5)(1+x+x2+...+x7)(x4+x5+...+x8)(x2+x3+...+x6) - 1-by-n的棋盘,涂四种颜色,红色为奇数,求h n h_nhn(指数生成函数套路)
- 求最大匹配与最小点覆盖
- 组合设计问题,根据MOLS生成BIBD,n=5
- 正方体着色问题,利用Playa公式计算