js前端可视化 | 单位平面向量旋转的数学原理与计算

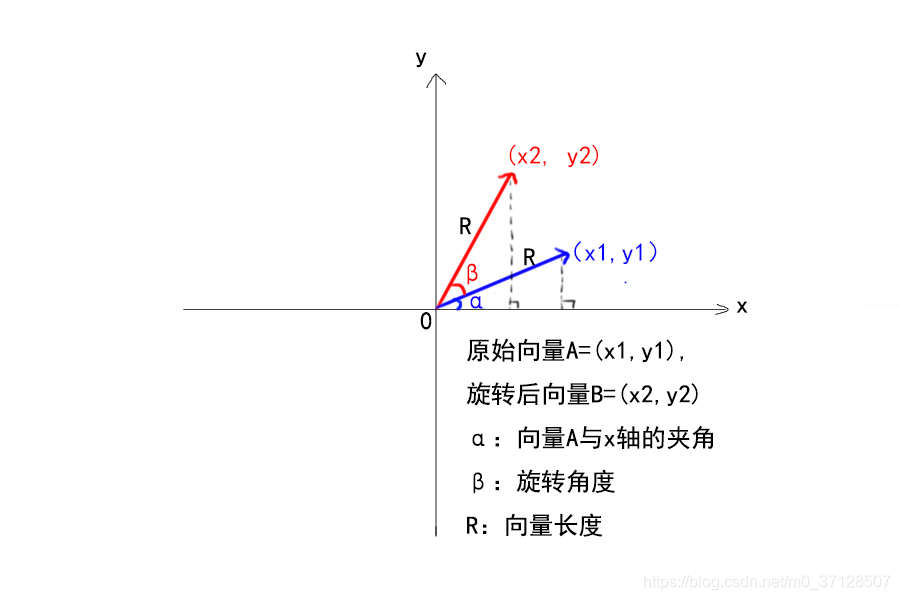
 一、平面向量旋转原理：

如上图所示，我们用坐标系表示向量，已知原始向量A=(x1, x2)， 旋转β角度后得到向量B=(x2, y2)，现在我们要求出向量B的坐标值。

此处我们设向量的长度R = 1；
根据三角函数公式，我们得出：
cosα  = x1 / R = x1 / 1 = x1; （邻边比斜边）
sinα = y1 / R = y1 / 1 = y2; （对边比斜边）
 

下面先回顾三角函数两角和差公式：
cos(α+β)=cosα·cosβ-sinα·sinβ （余余正正，符号反）
cos(α-β)=cosα·cosβ+sinα·sinβ

sin(α±β)=sinα·cosβ±cosα·sinβ （正余余正，符号同）

旋转后的向量角度等于 α+β
因此：=>
cos(α+β)= x2 / R = x2;
sin(α+β) = y2 / R = y2;

=> cos(α+β) = cosα·cosβ-sinα·sinβ = x2;
     sin(α+β) = sinα·cosβ + cosα·sinβ = y2;

得出 => x2 = x1 * cosβ - y1 * sinβ;
             y2 = y1 * cosβ  + x1 * sinβ;

最后我们可以得出向量B = (x1 * cosβ - y1 * sinβ, y1 * cosβ  + x1 * sinβ)
 

二、js平面向量旋转代码示例：

let x1 = 1, y1 = 0;
let x2 = null, y2 = null;


//dir : 旋转角度
function rotate(dir)
{
    x2 = x1 * Math.cos(dir) - y1 * Math.sin(dir);    
    y2 = y1 * Math.cos(dir) + x1 * Math.sin(dir);
}

rotate(Math.PI/4);
console.log(x2, y2);